
Historische achtergrond van analytische meetkunde

De Historische achtergrond van analytische meetkunde ze dateren uit de zeventiende eeuw, toen Pierre de Fermat en René Descartes hun fundamentele idee definieerden. Zijn uitvinding volgde op de modernisering van de algebra en algebraïsche notatie van François Viète..
Dit veld heeft zijn basis in het oude Griekenland, vooral in de werken van Apollonius en Euclides, die een grote invloed hadden op dit gebied van de wiskunde..
Het essentiële idee achter analytische geometrie is dat een relatie tussen twee variabelen, zodat de ene een functie is van de andere, een curve definieert. Dit idee werd voor het eerst ontwikkeld door Pierre de Fermat. Dankzij dit essentiële raamwerk konden Isaac Newton en Gottfried Leibniz de calculus ontwikkelen.
De Franse filosoof Descartes ontdekte ook een algebraïsche benadering van meetkunde, blijkbaar op zijn eentje. Descartes 'werk over geometrie komt voor in zijn beroemde boek Verhandeling van de methode.
Dit boek wijst erop dat het kompas en de geometrische constructies met rechte randen optellen, aftrekken, vermenigvuldigen en vierkantswortels omvatten..
Analytische meetkunde vertegenwoordigt de vereniging van twee belangrijke tradities in de wiskunde: meetkunde als de studie van vorm, en rekenen en algebra, die te maken hebben met kwantiteit of getallen. Daarom is analytische geometrie de studie van het gebied van geometrie met behulp van coördinatensystemen.
Verhaal
Achtergrond van analytische meetkunde
De relatie tussen meetkunde en algebra is in de geschiedenis van de wiskunde geëvolueerd, hoewel meetkunde een eerder stadium van volwassenheid bereikte.
De Griekse wiskundige Euclides kon bijvoorbeeld veel resultaten in zijn klassieke boek ordenen De elementen.
Maar het was de oude Griek Apollonius van Perga die in zijn boek de ontwikkeling van analytische meetkunde voorspelde Kegelsneden. Hij definieerde een kegelsnede als de kruising tussen een kegel en een vlak.
Met behulp van Euclides resultaten op soortgelijke driehoeken en secanten van cirkels, vond hij een relatie die wordt gegeven door de afstanden van elk punt "P" van een kegelsnede tot twee loodrechte lijnen, de hoofdas van een kegelsnede, en de raaklijn aan een eindpunt van de as. . Apollonius gebruikte deze relatie om fundamentele eigenschappen van de kegelsneden af te leiden.
De daaropvolgende ontwikkeling van coördinatensystemen in de wiskunde kwam pas op gang nadat de algebra volwassen was geworden dankzij islamitische en Indiase wiskundigen..
Tot de Renaissance werd geometrie gebruikt om oplossingen voor algebraïsche problemen te rechtvaardigen, maar algebra kon niet veel bijdragen aan de meetkunde..
Deze situatie zou veranderen met de goedkeuring van een handige notatie voor algebraïsche relaties en de ontwikkeling van het concept van een wiskundige functie, wat nu mogelijk was.
Eeuw XVI
Aan het einde van de 16e eeuw introduceerde de Franse wiskundige François Viète de eerste systematische algebraïsche notatie, waarbij letters werden gebruikt om numerieke grootheden weer te geven, zowel bekende als onbekende..
Hij ontwikkelde ook krachtige algemene methoden voor het werken met algebraïsche uitdrukkingen en het oplossen van algebraïsche vergelijkingen..
Hierdoor waren wiskundigen niet volledig afhankelijk van geometrische figuren en geometrische intuïtie om problemen op te lossen..
Zelfs sommige wiskundigen begonnen af te zien van de standaard geometrische manier van denken, volgens welke lineaire variabelen van lengtes en vierkanten overeenkomen met gebieden, terwijl kubieke variabelen overeenkomen met volumes..
De eersten die deze stap zetten waren de filosoof en wiskundige René Descartes, en de advocaat en wiskundige Pierre de Fermat..
Basis van analytische meetkunde
Descartes en Fermat stichtten onafhankelijk analytische meetkunde tijdens de jaren 1630, waarbij ze Viète's algebra gebruikten voor de studie van locus.
Deze wiskundigen realiseerden zich dat algebra een krachtig instrument was in de meetkunde en vonden wat tegenwoordig bekend staat als analytische meetkunde uit..
Een doorbraak die ze bereikten, was Viète verslaan door letters te gebruiken om afstanden weer te geven die eerder variabel dan vast zijn..
Descartes gebruikte vergelijkingen om geometrisch gedefinieerde curven te bestuderen en benadrukte de noodzaak om rekening te houden met algemene algebraïsch-grafische curven van polynoomvergelijkingen in graden "x" en "y".
Fermat benadrukte van zijn kant dat elke relatie tussen de coördinaten "x" en "y" een curve bepaalt.
Met behulp van deze ideeën herstructureerde hij Apollonius 'uitspraken in algebraïsche termen en herstelde een deel van zijn verloren werk..
Fermat gaf aan dat elke kwadratische vergelijking in "x" en "y" in de standaardvorm van een van de kegelsneden kan worden geplaatst. Desondanks heeft Fermat zijn werk over dit onderwerp nooit gepubliceerd.
Dankzij hun vorderingen, wat Archimedes slechts met grote moeite kon oplossen en voor geïsoleerde gevallen, konden Fermat en Descartes snel en voor een groot aantal curven (nu bekend als algebraïsche curven) oplossen..
Maar zijn ideeën werden pas algemeen aanvaard door de inspanningen van andere wiskundigen in de tweede helft van de 17e eeuw..
Wiskundigen Frans van Schooten, Florimond de Beaune en Johan de Witt hielpen Decartes 'werk uit te breiden en voegden belangrijk aanvullend materiaal toe..
Invloed
In Engeland populariseerde John Wallis analytische meetkunde. Hij gebruikte vergelijkingen om de kegelsneden te definiëren en hun eigenschappen af te leiden. Hoewel hij vrijelijk negatieve coördinaten gebruikte, was het Isaac Newton die twee schuine assen gebruikte om het vlak in vier kwadranten te verdelen.
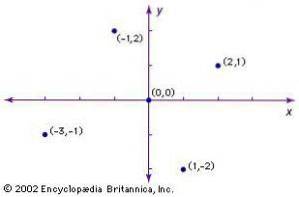
Newton en de Duitser Gottfried Leibniz brachten aan het einde van de 17e eeuw een revolutie teweeg in de wiskunde door onafhankelijk de kracht van calculus aan te tonen..
Newton demonstreerde het belang van analytische methoden in de meetkunde en hun rol in calculus, toen hij beweerde dat elke kubus (of elke derde graad algebraïsche curve) drie of vier standaardvergelijkingen heeft voor geschikte coördinaatassen. Met de hulp van Newton zelf bewees de Schotse wiskundige John Stirling het in 1717.
Analytische meetkunde van drie en meer dimensies
Hoewel zowel Descartes als Fermat voorstelden om drie coördinaten te gebruiken om krommen en oppervlakken in de ruimte te bestuderen, ontwikkelde de driedimensionale analytische geometrie zich langzaam tot 1730..
De wiskundigen Euler, Hermann en Clairaut produceerden algemene vergelijkingen voor cilinders, kegels en omwentelingsoppervlakken..
Euler gebruikte bijvoorbeeld vergelijkingen voor vertalingen in de ruimte om het algemene kwadratische oppervlak zo te transformeren dat de hoofdassen samenvallen met de coördinaatassen..
Euler, Joseph-Louis Lagrange en Gaspard Monge maakten analytische meetkunde onafhankelijk van synthetische (niet-analytische) meetkunde.
Referenties
- De ontwikkeling van analytische meetkunde (2001). Opgehaald van encyclopedia.com
- Geschiedenis van analytische meetkunde (2015). Opgehaald van maa.org
- Analyse (wiskunde). Opgehaald van britannica.com
- Analytische meetkunde. Opgehaald van britannica.com
- Descartes en de geboorte van analytische meetkunde. Opgehaald van sciencedirect.com


Niemand heeft nog op dit artikel gereageerd.