De boog, in de geometrie is het elke gebogen lijn die twee punten met elkaar verbindt. Een gebogen lijn is, in tegenstelling tot een rechte lijn, een lijn waarvan de richting op elk punt verschilt. Het tegenovergestelde van een boog is een segment, aangezien dit een recht stuk is dat twee punten met elkaar verbindt.
De boog die het meest in de geometrie wordt gebruikt, is de omtrekboog. Andere algemeen gebruikte bogen zijn de parabolische boog, de elliptische boog en de bovenleiding. De boogvorm wordt in de architectuur ook veel gebruikt als decoratief element en structureel element. Dit is het geval voor de lateien van de deuren en ramen, maar ook voor de bruggen en aquaducten.
Artikel index
De maat van een boog is de lengte, die afhangt van het type curve dat de twee punten en hun locatie met elkaar verbindt..
De lengte van een cirkelboog is een van de eenvoudigste om te berekenen, omdat de lengte van de volledige boog of omtrek van een omtrek bekend is.
De omtrek van een cirkel is twee pi keer je radio: p = 2 π R. Als u dit weet, als u de lengte wilt berekenen s van een cirkelvormige hoek α (gemeten in radialen) en straal R, er wordt een verhouding toegepast:
(s / p) = (α / 2 π)
Dan opruimen s van de vorige uitdrukking en het vervangen van de omtrek p door zijn uitdrukking als functie van de straal R, jij hebt:
s = (α / 2 π) p = (α / 2 π) (2 π R) = α R.
Dat wil zeggen, de maat van een cirkelboog is het product van de hoekopening maal de straal van de cirkelboog.
Voor een boog in het algemeen is het probleem ingewikkelder, tot het punt dat de grote denkers uit de oudheid bevestigden dat het een onmogelijke taak was..
Pas met de komst van de differentiaal- en integraalrekening in 1665 werd het probleem van het meten van een boog naar tevredenheid opgelost..
Vóór de uitvinding van differentiaalrekening konden oplossingen alleen worden gevonden door veelhoekige lijnen of omtrekbogen te gebruiken die de ware boog benaderden, maar deze oplossingen waren niet exact.
Vanuit het oogpunt van geometrie worden bogen geclassificeerd volgens de gebogen lijn die twee punten op het vlak met elkaar verbindt. Er zijn andere classificaties volgens hun gebruik en architectonische vorm.
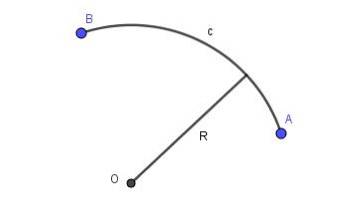
Als de lijn die twee punten van het vlak met elkaar verbindt een stuk omtrek van een bepaalde straal is, hebben we een cirkelvormige boog. Figuur 2 toont een cirkelboog c met straal R die de punten A en B verbindt.
De parabool is het pad dat wordt gevolgd door een object dat schuin in de lucht is gegooid. Als de curve die twee punten met elkaar verbindt een parabool is, dan hebben we een parabolische boog zoals getoond in figuur 3.
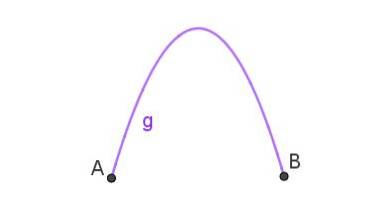
Dit is de vorm van de waterstraal die uit een naar boven wijzende slang komt. De parabolische boog is te zien in de waterbronnen.
De bovenleiding is een andere natuurlijke boog. De bovenleiding is de curve die van nature ontstaat wanneer een ketting of touw losjes aan twee afzonderlijke punten hangt.
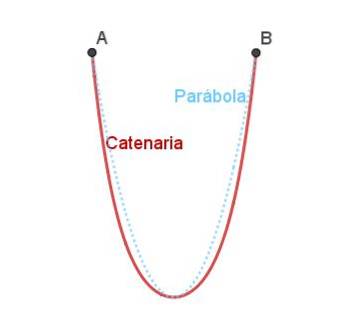
De bovenleiding is vergelijkbaar met de parabool, maar is niet precies hetzelfde als te zien is in figuur 4.
De omgekeerde bovenleiding wordt in de architectuur gebruikt als een structureel element met hoge druksterkte. In feite kan worden aangetoond dat het het sterkste type boog is van alle mogelijke vormen..
Om een stevige bovenleiding te bouwen, kopieert u gewoon de vorm van een hangend touw of ketting, waarna de gekopieerde vorm wordt omgedraaid om deze op de deur- of raamlateibalk te reproduceren.
Een boog is elliptisch als de kromme die twee punten verbindt een stuk of een gedeelte van een ellips is. De ellips wordt gedefinieerd als de meetkundige plaats van de punten waarvan de afstand tot twee gegeven punten altijd een constante hoeveelheid is.
De ellips is een curve die in de natuur voorkomt: het is de curve van het traject van de planeten rond de zon, zoals aangetoond door Johannes Kepler in het jaar 1609.
In de praktijk kan een ellips worden getekend door twee stutten op de grond of twee pinnen op papier vast te pinnen en er een touwtje aan te knopen. Het touw wordt vervolgens opgespannen met de marker of potlood en de curve wordt getraceerd. Een stuk ellips is een elliptische boog. De volgende animatie illustreert hoe de ellips wordt getekend:
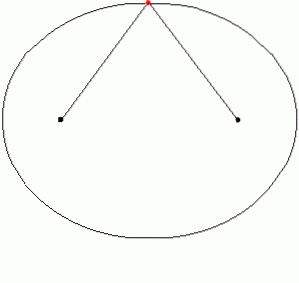
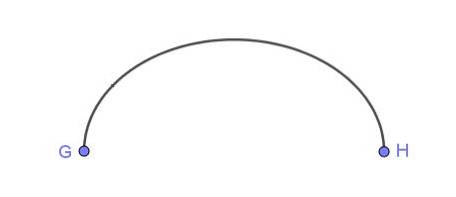
Figuur 6 toont een elliptische boog die de punten G en H verbindt.
De volgende voorbeelden hebben betrekking op het berekenen van de omtrek van bepaalde bogen.
Figuur 7 toont een raam afgewerkt in een uitgesneden cirkelvormige boog. De afmetingen in de afbeelding zijn in voet. Bereken de lengte van de boog.
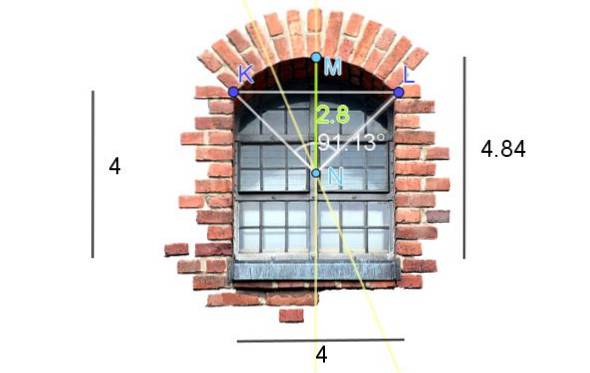
Om het middelpunt en de straal van de cirkelboog van de raamlateibalk te krijgen, zijn op de afbeelding de volgende constructies gemaakt:
-Het segment KL wordt getekend en de middelloodlijn wordt getekend.
-Daarna wordt het hoogste punt van de bovendorpel gelokaliseerd, dat we M noemen. Vervolgens wordt het segment KM bekeken en wordt zijn middelste getraceerd..
Het snijpunt van de twee middelloodlijnen is punt N en het is ook het middelpunt van de cirkelboog.
-Nu moeten we de lengte van het segment NM meten, die samenvalt met de straal R van de cirkelboog: R = 2,8 voet.
-Om naast de straal ook de lengte van de boog te kennen, is het noodzakelijk om de hoek te kennen die de boog vormt. Dat kan op twee manieren worden bepaald: het wordt gemeten met een gradenboog, of het wordt berekend met behulp van trigonometrie.
In het weergegeven geval is de hoek die wordt gevormd door de boog 91,13º, die moet worden omgezet in radialen:
91,13º = 91,13º * π / 180º = 1,59 radialen
Ten slotte berekenen we de lengte s van de boog met behulp van de formule s = α R.
s = 1,59 * 2,8 voet = 4,45 voet
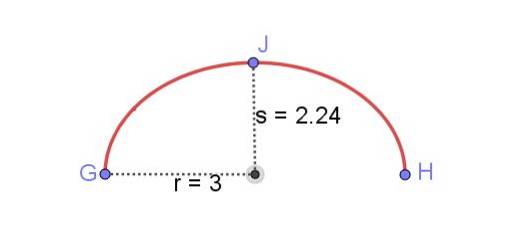
Zoek de lengte van de elliptische boog die wordt weergegeven in figuur 8, waarbij u de semi-hoofdas kent r en de semi-kleine as s van de ellips.
Het vinden van de lengte van een ellips was lange tijd een van de moeilijkste problemen in de wiskunde. U kunt oplossingen krijgen die worden uitgedrukt door elliptische integralen, maar om een numerieke waarde te hebben, moet u deze integralen uitbreiden in machtreeksen. Een exact resultaat zou oneindig veel termen van die reeksen vereisen.
Gelukkig vond het hindoeïstische wiskundige genie Ramanujan, die leefde tussen 1887 en 1920, een formule die heel precies de omtrek van een ellips benadert:
Omtrek van een ellips = π [3 (r + s) - √ ((3r + s) (r + 3s))]
De omtrek van een ellips met r = 3 cm en s = 2,24 cm is 16,55 cm. De getoonde elliptische boog heeft echter de helft van die waarde:
Lengte elliptische boog GH = 8,28 cm.
Niemand heeft nog op dit artikel gereageerd.