
Axiale belasting hoe het wordt berekend en oefeningen worden opgelost
De axiale belasting Het is de kracht die parallel is gericht aan de symmetrieas van een element waaruit een constructie bestaat. De axiale kracht of belasting kan spanning of compressie zijn. Als de werkingslijn van de axiale kracht samenvalt met de symmetrieas die door het zwaartepunt van het beschouwde element gaat, dan wordt er gezegd dat het een concentrische axiale belasting of kracht is..
Als het daarentegen een axiale kracht of belasting is die evenwijdig is aan de symmetrieas, maar waarvan de actielijn niet op de as zelf ligt, is het een excentrische axiale kracht.
-
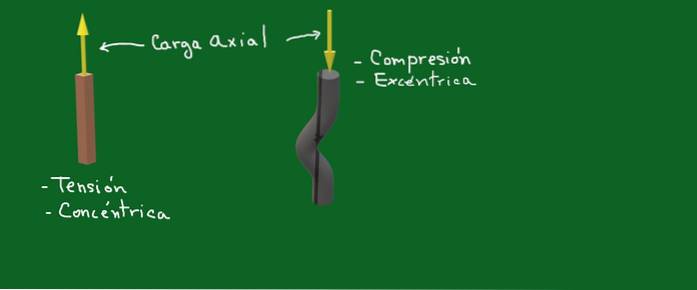
Figuur 1. Axiale belasting. Bron: zelf gemaakt
In figuur 1 geven de gele pijlen axiale krachten of belastingen weer. In het ene geval is het een concentrische spankracht en in het andere geval hebben we te maken met een excentrische compressiekracht.
De maateenheid voor axiale belasting in het internationale SI-systeem is de Newton (N). Maar ook andere krachteenheden zoals kilogramkracht (kg-f) en pondkracht (lb-f) worden vaak gebruikt..
Artikel index
- 1 Hoe wordt het berekend?
- 1.1 Relatie tussen axiale belasting en normale spanning
- 2 Opgeloste oefeningen
- 2.1 -Oefening 1
- 2.2 -Oefening 2
- 3 referenties
Hoe wordt het berekend?
Om de waarde van de axiale belasting in de elementen van een constructie te berekenen, moeten de volgende stappen worden gevolgd:
- Maak het krachtdiagram op elk element.
- Pas de vergelijkingen toe die een translationeel evenwicht garanderen, dat wil zeggen dat de som van alle krachten nul is.
- Overweeg de vergelijking van koppels of momenten zodat aan het rotatie-evenwicht wordt voldaan. In dit geval moet de som van alle koppels nul zijn.
- Bereken de krachten en identificeer de krachten of axiale belastingen in elk van de elementen.
Verhouding van axiale belasting tot normale spanning
De gemiddelde normale spanning wordt gedefinieerd als de verhouding van de axiale belasting gedeeld door het dwarsdoorsnedegebied. De eenheden van normale inspanning in het International System S.I. ze zijn Newton over vierkante meter (N / m²) of Pascal (Pa). De volgende afbeelding 2 illustreert voor de duidelijkheid het concept van normale spanning..
-
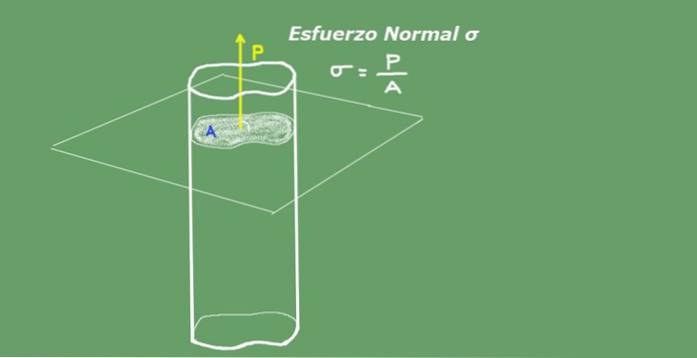
Figuur 2. Normale spanning. Bron: zelf gemaakt.
Opgeloste oefeningen
-Oefening 1
Beschouw een cilindrische betonnen kolom met hoogte h en straal r. Stel dat de dichtheid van beton ρ is. De kolom ondersteunt geen andere belasting dan zijn eigen gewicht en wordt ondersteund op een rechthoekige basis.
- Zoek de waarde van de axiale belasting op de punten A, B, C en D, die zich op de volgende posities bevinden: A aan de voet van de kolom, B a ⅓ hoogte h, C a ⅔ hoogte h en laatste D op de bovenkant van de kolom.
- Bepaal ook de gemiddelde normale spanning op elk van deze posities. Neem de volgende numerieke waarden: h = 3m, r = 20cm en ρ = 2250 kg / m³
-
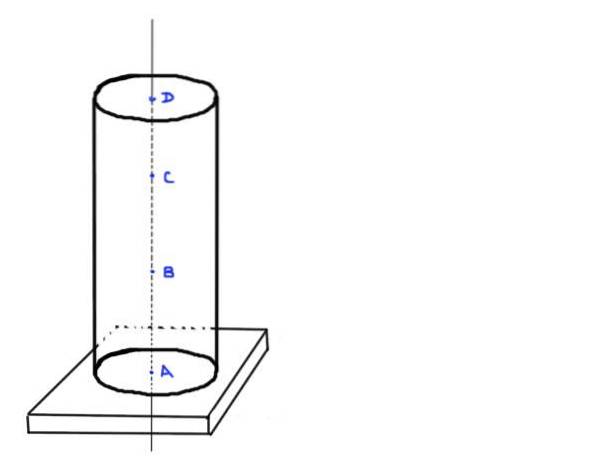
Figuur 3. Cilindrische kolom. Bron: zelf gemaakt.
Oplossing
Totaal kolomgewicht
Het totale gewicht W van de kolom is het product van de dichtheid maal het volume vermenigvuldigd met de versnelling van de zwaartekracht:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N
Axiale belasting in A
Op punt A moet de kolom zijn volledige gewicht dragen, dus de axiale belasting op dit punt is compressie is gelijk aan het gewicht van de kolom:
PA = W = 8313 N
Axiale belasting bij B
Slechts ⅔ van de kolom komt op punt B, dus de axiale belasting op dat punt is compressie en de waarde ⅔ het gewicht van de kolom:
PB = ⅔ W = 5542 N
Figuur 3. Cilindrische kolom. Bron: zelf gemaakt.
Boven positie C is er slechts ⅓ van de kolom, dus de axiale compressiebelasting is ⅓ van zijn eigen gewicht:
PC = ⅓ W = 2771 N
Axiale belasting in D
Ten slotte is er geen belasting op punt D, het bovenste uiteinde van de kolom, dus de axiale kracht op dat punt is nul..
PD = 0 N
Normale inspanningen in elk van de posities
Om de normale spanning in elk van de posities te bepalen, moet de doorsnede van gebied A worden berekend, die wordt gegeven door:
A = π ∙ r² = 0,126m²
Op deze manier zal de normaalspanning in elk van de posities het quotiënt zijn tussen de axiale kracht in elk van de punten gedeeld door het reeds berekende dwarsdoorsnedegebied, wat in deze oefening hetzelfde is voor alle punten omdat het een kolom cilindrisch.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Oefening 2
De figuur toont een structuur die bestaat uit twee balken die we AB en CB zullen noemen. Stang AB wordt aan uiteinde A ondersteund door een pen en aan het andere uiteinde verbonden met de andere staaf door een andere pen B.
Evenzo wordt de staaf CB aan het einde C ondersteund door middel van een pen en aan het einde B met de pen B die hem met de andere staaf verbindt. Een verticale kracht of belasting F wordt uitgeoefend op pin B, zoals weergegeven in de volgende afbeelding:
-
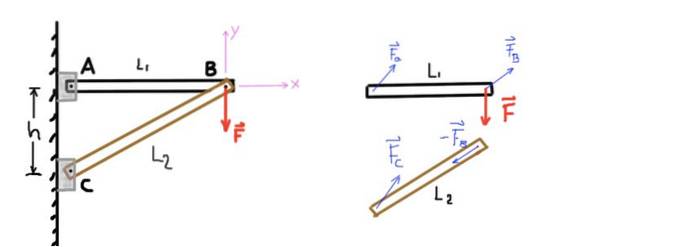
Figuur 4. Structuur met twee staven en diagram van het vrije lichaam. Bron: zelf gemaakt.
Neem aan dat het gewicht van de staven verwaarloosbaar is, aangezien de kracht F = 500 kg-f veel groter is dan het gewicht van de constructie. De afstand tussen steun A en C is h = 1,5 m en de lengte van de staaf AB is L1 = 2 m. Bepaal de axiale belasting op elk van de staven en geef aan of het een compressie- of trek-axiale belasting is.
Oplossing 2
De figuur toont door middel van een vrijlichaam-diagram de krachten die op elk van de elementen van de constructie inwerken. Ook wordt aangegeven met welk Cartesiaans coördinatensysteem de krachtevenwichtsvergelijkingen worden vastgesteld..
Koppels of momenten worden berekend op punt B en worden als positief beschouwd als ze van het scherm af wijzen (Z-as). De balans van krachten en koppels voor elke staaf is:
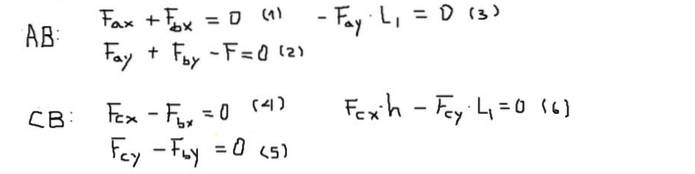
Vervolgens worden de componenten van de krachten van elk van de vergelijkingen in de volgende volgorde opgelost:
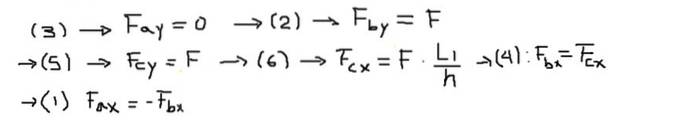
Ten slotte worden de resulterende krachten aan de uiteinden van elke staaf berekend:
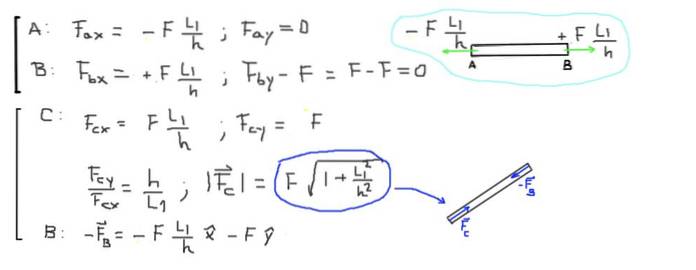
F ∙ (L1 / h) = 500 kg-f ∙ (2,0 m / 1,5 m) = 666,6 kg-f = 6533,3 N
De staaf CB is in compressie vanwege de twee krachten die aan de uiteinden werken die evenwijdig zijn aan de staaf en naar het midden wijzen. De grootte van de axiale compressiekracht in de staaf CB is:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1.5) ²) 1/2 = 833,3 kg-f = 8166,6 N
Referenties
- Beer F… Mechanica van materialen. 5e. Editie. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Mechanica van materialen. Achtste editie. Prentice Hall. 2011. 3-60.
- Gere J. Mechanica van materialen. Achtste editie. Cengage leren. 4-220.
- Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6e editie Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Opmerkingen over algemene fysica. UNAM. 87-98.



Niemand heeft nog op dit artikel gereageerd.