
Chi-kwadraat (χ²) verdeling, hoe deze te berekenen, voorbeelden
Het bewijs Chi in het kwadraat of chikwadraat (χtwee, waarbij χ de Griekse letter is genaamd "chi") wordt gebruikt om het gedrag van een bepaalde variabele te bepalen en ook als je wilt weten of twee of meer variabelen statistisch onafhankelijk zijn.
Om het gedrag van een variabele te controleren, wordt de uit te voeren test aangeroepen chi-kwadraattest van pasvorm. Om erachter te komen of twee of meer variabelen statistisch onafhankelijk zijn, wordt de test aangeroepen chi-vierkant van onafhankelijkheid, ook wel genoemd onvoorziene.
Deze tests maken deel uit van de statistische beslissingstheorie, waarin een populatie wordt bestudeerd en daarover beslissingen worden genomen, waarbij een of meer steekproeven worden geanalyseerd. Dit vereist het maken van bepaalde aannames over de variabelen, genaamd hypothese, wat al dan niet waar kan zijn.
Er zijn enkele tests om deze vermoedens te contrasteren en te bepalen welke geldig zijn, binnen een bepaalde vertrouwensmarge, waaronder de chikwadraattoets, die kan worden toegepast om twee en meer populaties te vergelijken..
Zoals we zullen zien, worden gewoonlijk twee soorten hypothesen opgeworpen over een populatieparameter in twee steekproeven: de nulhypothese, genaamd Hof (de steekproeven zijn onafhankelijk), en de alternatieve hypothese, aangeduid als H1, (de monsters zijn gecorreleerd), wat het tegenovergestelde is.
Artikel index
- 1 Wanneer wordt de chikwadraattoets gebruikt?
- 1.1 Voorwaarden om het toe te passen
- 2 Chi-kwadraatverdeling
- 2.1 Vrijheidsgraden
- 2.2 Formulering van hypothesen
- 3 Hoe wordt de chikwadraattatistiek berekend?
- 3.1 Acceptatiecriteria voor Ho
- 4 Rekenvoorbeeld
- 5 referenties
Wanneer wordt de chikwadraattoets gebruikt?
De chi-kwadraat-test wordt toegepast op variabelen die eigenschappen beschrijven, zoals geslacht, burgerlijke staat, bloedgroep, oogkleur en voorkeuren van verschillende typen.
De test is bedoeld als u:
-Controleren of een distributie geschikt is om een variabele te beschrijven, die wordt aangeroepen goedheid van fit. Met behulp van de chikwadraattoets is het mogelijk om te weten of er significante verschillen zijn tussen de geselecteerde theoretische verdeling en de waargenomen frequentieverdeling..
-Weet of twee variabelen X en Y onafhankelijk zijn vanuit statistisch oogpunt. Dit staat bekend als onafhankelijkheidstest.
Omdat het wordt toegepast op kwalitatieve of categorische variabelen, wordt de chikwadraattoets veel gebruikt in sociale wetenschappen, management en geneeskunde..
Voorwaarden om het toe te passen
Er zijn twee belangrijke vereisten om het correct toe te passen:
-De gegevens moeten in frequenties worden gegroepeerd.
-De steekproef moet groot genoeg zijn om de chikwadraatverdeling geldig te laten zijn, anders wordt de waarde overschat en leidt dit tot de verwerping van de nulhypothese, terwijl dit niet het geval zou moeten zijn..
De algemene regel is dat als een frequentie met een waarde kleiner dan 5 voorkomt in de gegroepeerde gegevens, deze niet wordt gebruikt. Als er meer dan één frequentie kleiner is dan 5, moeten ze worden gecombineerd tot één om een frequentie te verkrijgen met een numerieke waarde groter dan 5.
Chi-kwadraatverdeling
χtwee het is een continue verdeling van kansen. Eigenlijk zijn er verschillende curves, afhankelijk van een parameter k gebeld graden van vrijheid van de willekeurige variabele.
De eigenschappen zijn:
-Het gebied onder de curve is gelijk aan 1.
-De waarden van χtwee ze zijn positief.
-De verdeling is asymmetrisch, dat wil zeggen, het heeft een vertekend beeld.
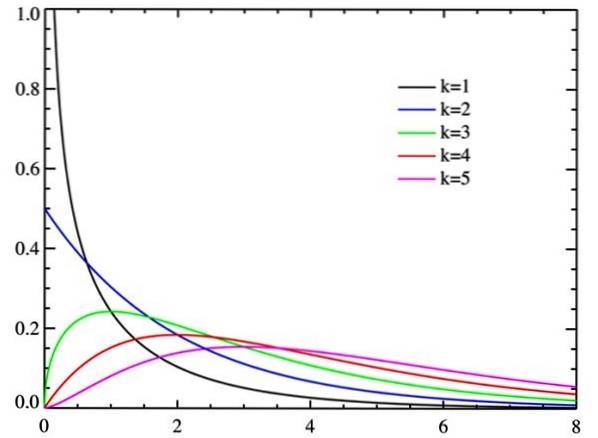
Graden van vrijheid
Naarmate de vrijheidsgraden toenemen, neigt de chikwadraatverdeling naar normaliteit, zoals te zien is in de figuur.
Voor een bepaalde verdeling worden de vrijheidsgraden bepaald via de kruistabel, dat is de tabel waarin de waargenomen frequenties van de variabelen worden geregistreerd.
Als een tafel heeft F. rijen en c kolommen, de waarde van k het is:
k = (f - 1) ⋅ (c - 1)
Formulering van hypothesen
Als de chikwadraattoets geschikt is, worden de volgende hypothesen geformuleerd:
-H.of: de variabele X heeft een kansverdeling f (x) met de specifieke parameters y1, Ytwee…, Yp
-H.1: X heeft een andere kansverdeling.
De kansverdeling die in de nulhypothese wordt aangenomen, kan bijvoorbeeld de bekende normale verdeling zijn, en de parameters zijn de gemiddelde μ en de standaarddeviatie σ.
Bovendien wordt de nulhypothese geëvalueerd met een bepaald significantieniveau, dat wil zeggen een maatstaf voor de fout die zou worden begaan wanneer de nulhypothese als waar zou worden afgewezen.
Meestal wordt dit niveau ingesteld op 1%, 5% of 10% en hoe lager het is, hoe betrouwbaarder het testresultaat..
En als de chikwadraattoets van contingentie wordt gebruikt, die, zoals we al zeiden, dient om de onafhankelijkheid tussen twee variabelen X en Y te verifiëren, zijn de hypothesen:
-H.of: variabelen X en Y zijn onafhankelijk.
-H.1: X en Y zijn afhankelijk.
Nogmaals, het is noodzakelijk om een significantieniveau te specificeren om de maat van de fout te kennen bij het nemen van de beslissing..
Hoe wordt de chikwadraattatistiek berekend?
De chikwadraatstatistiek wordt als volgt berekend:

De sommatie wordt uitgevoerd van de eerste klasse i = 1 naar de laatste, namelijk i = k.
Bovendien:
-F.of is een waargenomen frequentie (komt uit de verkregen gegevens).
-F.en is de verwachte of theoretische frequentie (moet worden berekend op basis van de gegevens).
Om de nulhypothese te accepteren of te verwerpen, berekenen we χtwee voor de waargenomen gegevens en vergeleken met een aangeroepen waarde kritisch chi-vierkant, die afhangt van de vrijheidsgraden k en het significantieniveau α
χtweekritiek χtweek, α
Als we de test bijvoorbeeld willen uitvoeren met een significantieniveau van 1%, dan is α = 0,01, als het 5% wordt, dan α = 0,05 enzovoort. We definiëren p, de parameter van de distributie, als:
p = 1 - α
Deze kritische chikwadraatwaarden worden bepaald door tabellen met de cumulatieve oppervlaktewaarde. Bijvoorbeeld, voor k = 1, wat staat voor 1 vrijheidsgraad en α = 0,05, wat gelijk is aan p = 1 - 0,05 = 0,95, de waarde van χtwee is 3.841.

H acceptatiecriteriaof
Het criterium voor het accepteren van Hof het is:
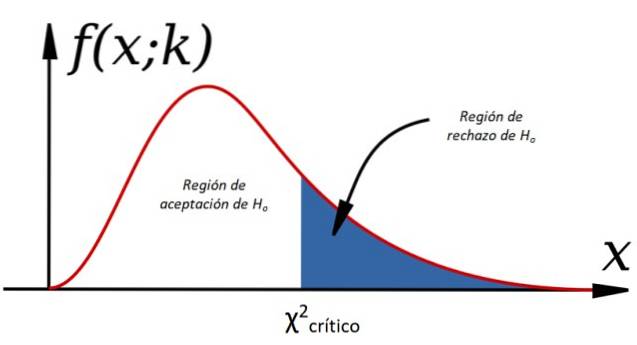
-Ja χtwee < χtweekritiek H wordt geaccepteerdof, anders wordt het afgewezen (zie figuur 1).
Rekenvoorbeeld
In de volgende toepassing zal de chi-kwadraattoets worden gebruikt als een test van onafhankelijkheid.
Stel dat de onderzoekers willen weten of de voorkeur voor zwarte koffie gerelateerd is aan het geslacht van de persoon, en specificeer het antwoord met een significantieniveau van α = 0,05.
Hiervoor is een steekproef van 100 mensen geïnterviewd en hun antwoorden zijn beschikbaar:
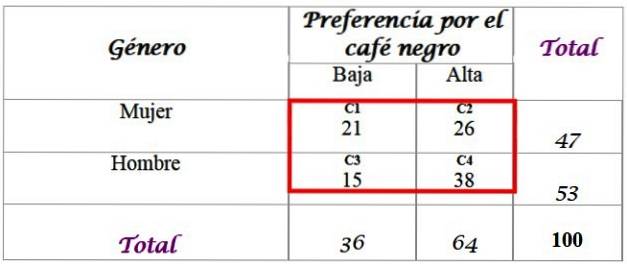
Stap 1
Stel de hypothesen vast:
-H.of: geslacht en voorkeur voor zwarte koffie zijn onafhankelijk.
-H.1: de smaak voor zwarte koffie is gerelateerd aan het geslacht van de persoon.
Stap 2
Bereken de verwachte frequenties voor de verdeling, waarvoor de totalen die in de laatste rij en in de rechterkolom van de tabel zijn opgeteld, vereist zijn. Elke cel in het rode vak heeft een verwachte waarde F.en, die wordt berekend door het totaal van uw rij F te vermenigvuldigen met het totaal van uw kolom C, gedeeld door het totaal van de steekproef N:
F.en = (F x C) / N
De resultaten zijn voor elke cel als volgt:
-C1: (36 x 47) / 100 = 16,92
-C2: (64 x 47) / 100 = 30,08
-C3: (36 x 53) / 100 = 19,08
-C4: (64 x 53) / 100 = 33,92
Stap 3
Vervolgens moet voor deze verdeling de chikwadraatstatistiek worden berekend volgens de gegeven formule:

Stap 4
Bepaal χtweekritiek, wetende dat de opgenomen gegevens zich in f = 2 rijen en c = 2 kolommen bevinden, is het aantal vrijheidsgraden daarom:
k = (2-1) ⋅ (2-1) = 1.
Wat betekent dat we in de bovenstaande tabel moeten zoeken naar de waarde van χtweek, α = χtwee1; 0,05 , dat is:
χtweekritiek = 3.841
Stap 5
Vergelijk de waarden en beslis:
χtwee = 2,9005
χtweekritiek = 3.841
Sinds χtwee < χtweekritiek de nulhypothese wordt geaccepteerd en er wordt geconcludeerd dat de voorkeur voor zwarte koffie niet gekoppeld is aan het geslacht van de persoon, met een significantieniveau van 5%.
Referenties
- Chi Square-test voor onafhankelijkheid. Hersteld van: saylordotorg.github.io.
- Med Wave. Statistieken toegepast op gezondheidswetenschappen: de chikwadraattoets. Hersteld van: medwave.cl.
- Waarschijnlijkheden en statistieken. Chi-square goodness-of-fit-test. Hersteld van: probayestadistica.com.
- Triola, M. 2012. Elementaire statistieken. 11e. Editie. Addison Wesley.
- UNAM. Chikwadraattoets. Hersteld van: asesorias.cuautitlan2.unam.mx.



Niemand heeft nog op dit artikel gereageerd.