
Significante cijfers regels, voorbeelden, opgeloste oefeningen
Is genaamd Significante cijfers tot het aantal cijfers in de mantisse van een nummer. Hoe meer nummers u heeft, hoe nauwkeuriger de hoeveelheid bekend is. Ter herinnering, de mantisse is het cijfer dat de macht van 10 vergezelt wanneer het nummer in wetenschappelijke notatie is geschreven..
Laten we bijvoorbeeld het getal 0,00376 nemen, dat wordt geschreven als 3,76 x 10 -3. De mantisse is 3,76 en het aantal heeft in totaal 3 significante cijfers. Het getal 0,129 heeft ook 3 significante cijfers, terwijl 4,5 er slechts 2 heeft.

En wat gebeurt er als het getal een geheel getal is? Het betekent dat het met zo veel mogelijk precisie bekend is, met andere woorden, het heeft een oneindige precisie. Als u bijvoorbeeld mensen, dieren of voorwerpen zoals boeken en telefoons telt, is het resultaat een nauwkeurig geheel getal.
Als we zeggen dat er in een bioscoop 110 mensen naar een film kijken, is dit het exacte aantal, niet meer en niet minder, en het heeft 3 significante cijfers.
Significante cijfers worden afgehandeld door enkele eenvoudige regels die met een beetje oefening uit het hoofd worden geleerd, zoals we hieronder zullen zien..
Artikel index
- 1 Regels voor het bepalen van de significante cijfers van een getal
- 1.1 Regel 1
- 1.2 Regel 3
- 1.3 Regel 4
- 1.4 Regel 5
- 2 voorbeelden
- 2.1 Voorbeeld 1
- 2.2 Voorbeeld 2
- 2.3 Voorbeeld 3
- 3 Regels voor het afronden van getallen
- 4 referenties
Regels voor het bepalen van de significante cijfers van een getal
Regel 1
De voorloopnullen tellen niet als een significant cijfer, dus 0,045 en 4,5 hebben beide 2 significante cijfers, aangezien deze beginnen te tellen vanaf de linkerkant en beginnend bij het eerste niet-nul cijfer.
Regel 2
De nullen achter (rechts) het eerste significante cijfer tellen wel als significant cijfer (zolang dit gerechtvaardigd wordt door de precisie van het meetinstrument).
Ten slotte worden de nullen in het midden ook als significant cijfer geteld..
Regel 3
Voor getallen die in wetenschappelijke notatie zijn geschreven, zijn alle cijfers in de mantisse significant en heeft de exponent geen invloed op de precisie..
Regel 4
Wanneer u bewerkingen met decimalen uitvoert, bijvoorbeeld bij het berekenen van oppervlakten of andere soortgelijke bewerkingen, moet het resultaat hetzelfde aantal significante cijfers hebben als de hoeveelheid met het minste aantal significante cijfers die aan de bewerking hebben deelgenomen. Deze regel is geldig voor elke rekenkundige bewerking.
Regel 5
Het teken van het nummer heeft geen invloed op het aantal significante cijfers.
We zullen hiervan meteen enkele voorbeelden zien en alle andere regels.
Voorbeelden
voorbeeld 1
Zoek uit hoeveel significante cijfers er in elk van deze cijfers zitten.
a) 876
b) 1000,68
c) 0,00005026
d) 4.8
e) -6,99
Antwoorden
a) 876 heeft 3 significante cijfers.
b) 1000.68 heeft 6 significante cijfers, aangezien de nullen ertussen als zodanig tellen.
c) In plaats daarvan heeft 0.00005026 4 significante cijfers. Merk op dat de 5 nullen links van de 5 niet als een significant cijfer worden geteld, maar de 0 die tussen 5 en 2 ligt..
d) 4.8 heeft 2 significante cijfers.
e) -6,99 heeft 3 significante cijfers.
Voorbeeld 2
Het is gebruikelijk om metingen uit te voeren met meetinstrumenten, zoals meetlinten, horloges, thermometers, weegschalen enzovoort. Met hoeveel significante cijfers moeten we de hoeveelheden rapporteren die we op deze manier meten??
Antwoord
Het hangt af van de waardering van het instrument waarmee het wordt gemeten. Laten we een voorbeeld nemen: meet de buitendiameter van een buis, met een liniaal met schaalverdeling en met een schuifmaat of schuifmaat.
De nonius is een instrument dat lengtes heel precies meet doordat het een extra kleine schaal heeft, genaamd nonius, die zorgt voor een grotere fijnheid, om zo te zeggen, bij het meten.
Het is nauwkeuriger dan een gegradueerde liniaal omdat we daarmee meer significante figuren van een bepaalde lengte kunnen weten.
Daarom heeft het geen zin om een omtrek van bijvoorbeeld 35,88 cm te rapporteren als we het meten met een meetlint, aangezien dit instrument niet nauwkeurig genoeg is om zoveel significante cijfers te rapporteren..
De waardering A van het meetlint wordt gegeven door:
Voorbeeld 3
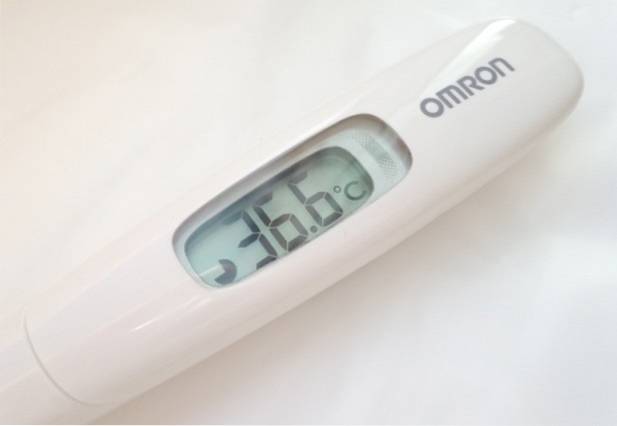
Hoeveel significante cijfers heeft de aflezing gemaakt met de digitale thermometer?
Antwoord
De thermometer in de afbeelding geeft temperatuurmetingen van drie cijfers weer. Bij de getoonde meting, 36,6 ºC, zijn echter alleen de eerste twee cijfers van links naar rechts nauwkeurig, aangezien het decimaalteken wordt beïnvloed door de waarderingsfout van het instrument, die meestal wordt aangegeven op de achterkant van het instrument of in uw bedieningshandleiding..
Het gebruikelijke bij het getoonde type digitaal instrument is een beoordelingsfout van 0,1 ºC. Dit is voldoende om er zeker van te zijn dat u geen koorts heeft..

Regels voor het afronden van getallen
Wanneer u een rekenmachine gebruikt om berekeningen uit te voeren met verkregen metingen, is het niet correct om het resultaat te geven met alle cijfers die op het scherm verschijnen.
Alleen degenen die precies bekend zijn, worden behouden, aangezien alleen die echte betekenis hebben. Het is dan nodig om de resultaten af te ronden zodat ze passen bij het aantal precies bekende cijfers. Deze regels zijn:
-Als het nummer dat volgt op het cijfer dat moet worden onthouden, is gelijk aan of groter dan 5, 1 wordt aan dit cijfer toegevoegd.
Als we bijvoorbeeld 3,786 afronden op twee decimalen, willen we de getallen tot 8 behouden. Aangezien het getal dat volgt op (6) groter is dan 5, wordt de 8 8 + 1 = 9 en blijft het getal 3,79.
-Wanneer het nummer dat volgt op het cijfer dat moet worden vastgehouden, is minder dan 5, het cijfer blijft hetzelfde.
Als we 1.27924 willen afronden zodat het slechts 3 decimalen heeft, wordt dit bereikt door 9 te bereiken, gevolgd door 2. Aangezien 2 kleiner is dan 5, verdwijnen deze decimalen en blijft het afgeronde getal 1,279.
Oefening opgelost
Een eettafel heeft de vorm en afmetingen zoals aangegeven in de bijgaande figuur. U wordt gevraagd om de oppervlakte te berekenen aan de hand van de bedrijfsregels met significante cijfers.
Oplossing
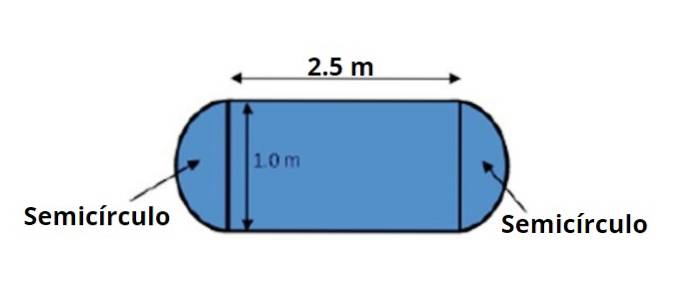
Het tafelgedeelte kan worden onderverdeeld in een centraal rechthoekig gebied en twee halve cirkels, een aan elke kant, die samen 1 volledige cirkel vormen.
We zullen A bellen1 naar de oppervlakte van de rechthoek, gegeven door:
NAAR1 = basis × hoogte = 2,5 m x 1,0 m = 2,5 mtwee
Van zijn kant is het oppervlak van de cirkel, dat gelijk is aan dat van 1 halve cirkel vermenigvuldigd met 2:
NAARtwee = π × straaltwee
De diameter van een van de halve cirkels is 1,0 m, daarom is de straal 0,50 m. De diameter kan ook direct worden gebruikt om de oppervlakte te berekenen, in dit geval:
NAARtwee = (π × diametertwee) / 4
In elk geval:
NAARtwee = [π x (1,0 m)twee] / 4 = 0,785398163 mtwee
Alle cijfers van de rekenmachine zijn gebruikt. Nu voegen we A toe1 nu altwee voor de totale oppervlakte A van de tafel:
A = (2,5 + 0,785398163) mtwee = 3,285398163 mtwee
Aangezien de afmetingen van de tabel bekend zijn bij 2 significante cijfers, heeft het geen zin om het resultaat uit te drukken met alle decimalen gegeven door de rekenmachine, die nooit het aantal significante cijfers van een resultaat geeft.
Wat u moet doen, is het gebied afronden zodat het hetzelfde aantal significante cijfers heeft als de afmetingen van de tafel, dat wil zeggen 2. Daarom wordt het eindresultaat als volgt gerapporteerd:
A = 3,3 mtwee
Referenties
- Bauer, W. 2011. Physics for Engineering and Sciences. Deel 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Bewerkt door Douglas Figueroa (USB).
- Fisicalab. Significante cijfers en afronding. Hersteld van: fisicalab.com.
- Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6e. Ed Prentice Hall.
- Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. Ed. Deel 1.



Niemand heeft nog op dit artikel gereageerd.