
Congruentie congruente cijfers, criteria, voorbeelden, oefeningen
De congruentie, In de geometrie wijst het erop dat als twee vlakke figuren dezelfde vorm en afmetingen hebben, ze congruent zijn. Twee segmenten zijn bijvoorbeeld congruent als hun lengte gelijk is. Evenzo hebben congruente hoeken dezelfde maat, ook al zijn ze niet op dezelfde manier in het vlak georiënteerd..
De term "congruentie" komt uit het Latijn congruent, waarvan de betekenis correspondentie is. Twee congruente figuren komen dus exact met elkaar overeen..
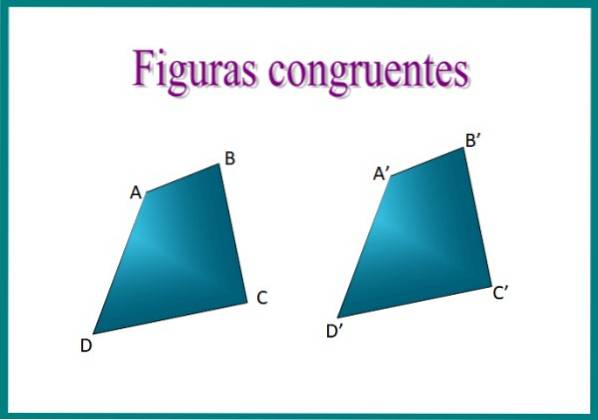
Als we bijvoorbeeld de twee vierhoeken in de afbeelding over elkaar heen leggen, zullen we zien dat ze congruent zijn, aangezien de rangschikking van hun zijden identiek is en ze hetzelfde meten.
Door vierhoeken ABCD en A'B'C'D 'op elkaar te plaatsen, komen de cijfers exact overeen. De bijpassende kanten worden genoemd homologe kanten of overeenkomend en om congruentie uit te drukken wordt het symbool ≡ gebruikt. Dan kunnen we stellen dat ABCD ≡ A'B'C'D '.
Artikel index
- 1 Congruentiecriteria
- 1.1 Congruentie, identiteit en gelijkenis
- 2 Voorbeelden van congruentie
- 2.1 - Hoekcongruentie
- 2.2 - Congruentie van driehoeken
- 3 Opgeloste oefeningen
- 3.1 - Oefening 1
- 3.2 - Oefening 2
- 4 referenties
Congruentiecriteria
De volgende kenmerken zijn gemeenschappelijk voor congruente polygonen:
-Zelfde vorm en maat.
-Identieke maten van hun hoeken.
-Dezelfde maat aan elk van zijn zijden.
In het geval dat twee polygonen in kwestie regelmatig zijn, dat wil zeggen dat alle zijden en interne hoeken hetzelfde meten, is congruentie verzekerd wanneer eraan is voldaan sommige van de volgende voorwaarden:
-De zijkanten zijn congruent
-De apothems ze hebben dezelfde maat
-De radio- van elke veelhoek meet gelijk
Het apothema van een regelmatige veelhoek is de afstand tussen het midden en een van de zijkanten, terwijl de straal overeenkomt met de afstand tussen het midden en een hoekpunt of hoek van de figuur.
Congruentiecriteria worden vaak gebruikt omdat zoveel onderdelen en stukken van alle soorten in massa worden geproduceerd en dezelfde vorm en afmetingen moeten hebben. Op deze manier kunnen ze indien nodig eenvoudig worden vervangen, bijvoorbeeld moeren, bouten, platen of de stoeptegels op de grond in de straat..

Congruentie, identiteit en gelijkenis
Er zijn bijvoorbeeld geometrische concepten die verband houden met congruentie identieke figuren en de vergelijkbare cijfers, dat wil niet per se zeggen dat de cijfers congruent zijn.
Merk op dat de congruente figuren identiek zijn, maar de vierhoeken in figuur 1 zouden op verschillende manieren in het vlak kunnen worden georiënteerd en toch congruent blijven, aangezien de verschillende oriëntatie de grootte van hun zijden of hun hoeken niet verandert. In dat geval zouden ze niet langer identiek zijn.
Het andere concept is dat van de gelijkenis van figuren: twee vlakke figuren zijn vergelijkbaar als ze dezelfde vorm hebben en hun interne hoeken hetzelfde meten, hoewel de grootte van de figuren kan verschillen. Als dit het geval is, zijn de cijfers niet congruent.
Voorbeelden van congruentie
- Hoekcongruentie
Zoals we aan het begin hebben aangegeven, hebben congruente hoeken dezelfde maat. Er zijn verschillende manieren om congruente hoeken te verkrijgen:
voorbeeld 1
Twee lijnen met een gemeenschappelijk punt definiëren twee hoeken, genaamd Tegenovergestelde hoeken bij het hoekpunt. Deze hoeken hebben dezelfde maat, daarom zijn ze congruent.
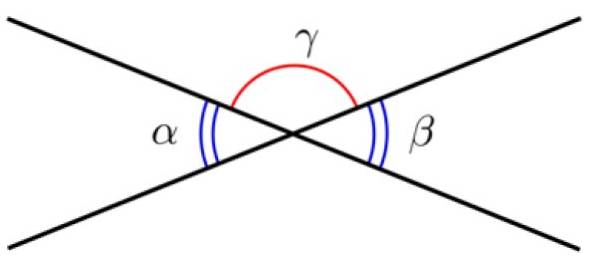
Voorbeeld 2
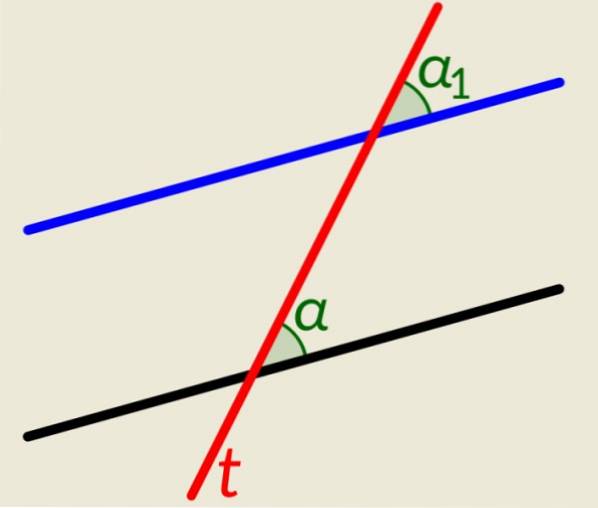
Er zijn twee parallelle lijnen plus één lijn t dat ze allebei doorsnijdt. Net als in het vorige voorbeeld, wanneer deze lijn de parallellen snijdt, genereert het congruente hoeken, één op elke lijn aan de rechterkant en nog twee aan de linkerkant. De figuur toont α en α1, rechts van de lijn t, die congruent zijn.
Voorbeeld 3
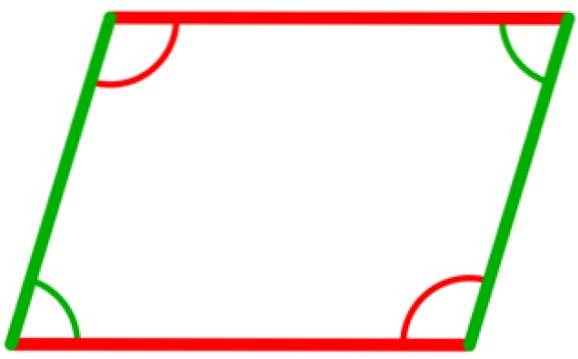
In een parallellogram zijn er vier binnenhoeken, die twee tot twee congruent zijn. Dit zijn de hoeken die zich tussen tegenoverliggende hoekpunten bevinden, zoals weergegeven in de volgende afbeelding, waarin de twee hoeken in groen congruent zijn, evenals de twee hoeken in rood.
- Congruentie van driehoeken
Twee driehoeken van dezelfde vorm en grootte zijn congruent. Om dit te verifiëren, zijn er drie criteria die kunnen worden onderzocht op zoek naar congruentie:
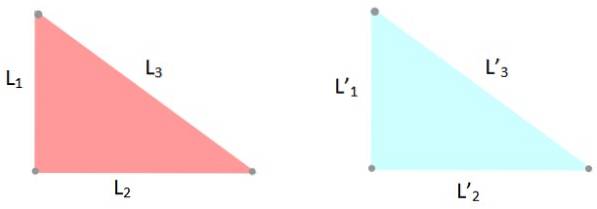
-Criterium LLL: de drie zijden van de driehoeken hebben dezelfde afmetingen, dus L1 = L '1L.twee = L 'twee en ik3 = L '3.
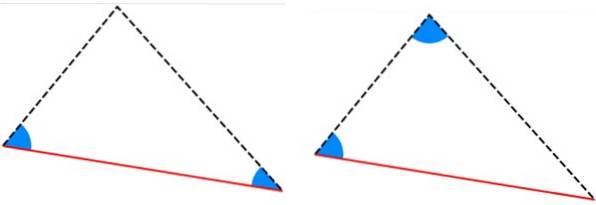
-ALA- en AAL-criteria: driehoeken hebben twee gelijke binnenhoeken en de zijde tussen die hoeken heeft dezelfde maat.
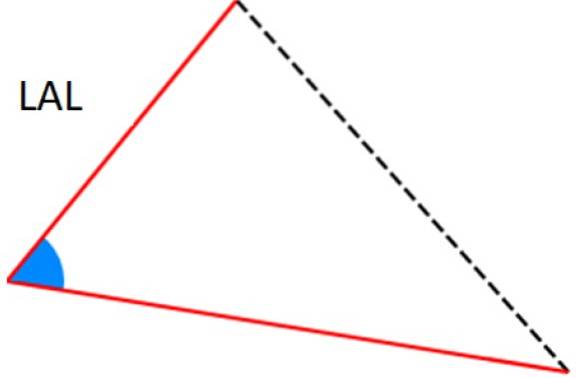
-LAL-criterium: twee van de zijkanten zijn identiek (corresponderend) en daartussen is er dezelfde hoek.
Opgeloste oefeningen
- Oefening 1
Twee driehoeken worden getoond in de volgende afbeelding: ΔABC en ΔECF. Het is bekend dat AC = EF, dat AB = 6 en dat CF = 10. Verder zijn de hoeken ∡BAC en ∡FEC congruent en de hoeken ∡ACB en ∡FCB ook congruent..
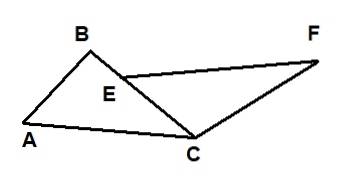
Dan is de lengte van segment BE gelijk aan:
(i) 5
(ii) 3
(iii) 4
(iv) 2
(v) 6
Oplossing
Aangezien de twee driehoeken een zijde hebben van gelijke lengte AC = EF tussen de gelijke hoeken ∡BAC = ∡CEF en ∡BCA = ∡CFE, kan worden gezegd dat de twee driehoeken congruent zijn volgens het ALA-criterium.
Dat wil zeggen, ΔBAC ≡ ΔCEF, dus we moeten:
BA = CE = AB = 6
BC = CF = 10
AC = EF
Maar het te berekenen segment is BE = BC - EC = 10 - 6 = 4.
Dus het juiste antwoord is (iii).
- Oefening 2
Drie driehoeken worden weergegeven in de onderstaande afbeelding. Het is ook bekend dat de twee aangegeven hoeken elk 80º meten en dat de segmenten AB = PD en AP = CD. Zoek de waarde van de hoek X die in de afbeelding wordt aangegeven.
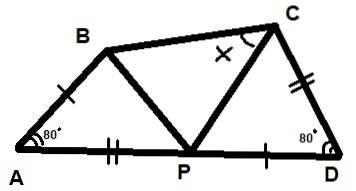
Oplossing
Je moet de eigenschappen van de driehoeken toepassen, die stap voor stap worden uitgewerkt.
Stap 1
Beginnend met het LAL-driehoekscongruentiecriterium, kan worden gesteld dat de BAP- en PDC-driehoeken congruent zijn:
ΔBAP ≡ ΔPDC
Stap 2
Het bovenstaande leidt tot bevestiging dat BP = PC, daarom is de driehoek ΔBPC gelijkbenig en ∡PCB = ∡PBC = X.
Stap 3
Als we de hoek BPC γ noemen, volgt dat:
2x + γ = 180º
Stap 4
En als we de hoeken APB en DCP β en α de hoeken ABP en DPC noemen, hebben we:
α + β + γ = 180º (aangezien APB een vlakke hoek is).
Stap 5
Verder α + β + 80º = 180º door de som van de binnenhoeken van de driehoek APB.
Stap 6
Door al deze uitdrukkingen te combineren, hebben we:
α + β = 100º
Stap 7
En daarom:
γ = 80º.
Stap 8
Ten slotte volgt daaruit dat:
2X + 80º = 180º
Met X = 50º.
Referenties
- Baldor, A. 1973. Vliegtuig- en ruimtegeometrie. Centraal-Amerikaanse culturele.
- Stichting CK-12. Congruente veelhoeken. Hersteld van: ck 12.org.
- Geniet van wiskunde. Definities: Radius (veelhoek). Hersteld van: gustolasmatematicas.com.
- Math Open Reference. Polygonen testen op congruentie. Hersteld van: mathopenref.com.
- Wikipedia. Congruentie (geometrie). Hersteld van: es.wikipedia.org.
- Zapata, F. Driehoeken, geschiedenis, elementen, classificatie, eigenschappen. Hersteld van: lifeder.com.



Niemand heeft nog op dit artikel gereageerd.