
Eindige set eigenschappen, voorbeelden, opgeloste oefeningen
Het wordt begrepen door eindige reeks elke set met een beperkt of telbaar aantal elementen. Voorbeelden van eindige sets zijn de knikkers die in een zak zitten, de set huizen in een buurt of de set P. gevormd door de eerste twintig (20) natuurlijke getallen:
P. = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Het aantal sterren in het universum is ongetwijfeld immens, maar het is niet zeker of het eindig of oneindig is. Het aantal planeten in het zonnestelsel is echter eindig.
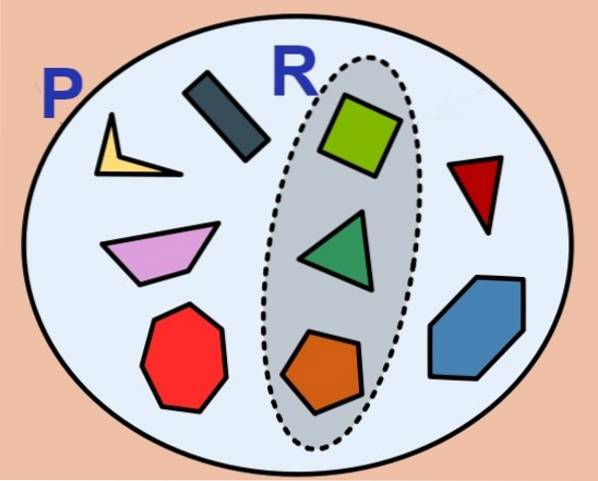
Het aantal elementen van een eindige verzameling wordt de kardinaliteit en voor de verzameling genoemd P. wordt als volgt aangeduid: Card (P.) of #P.. De lege set heeft een kardinaliteit nul en wordt als een eindige set beschouwd.
Artikel index
- 1 Eigenschappen
- 2 voorbeelden
- 2.1 Meer voorbeelden
- 3 Opgeloste oefeningen
- 3.1 Oefening 1
- 3.2 Oefening 2
- 3.3 Oefening 3
- 3.4 Oefening 4
- 4 referenties
Eigendommen
Onder de eigenschappen van eindige verzamelingen zijn de volgende:
1- De vereniging van eindige verzamelingen geeft aanleiding tot een nieuwe eindige verzameling.
2- Als twee eindige verzamelingen elkaar kruisen, resulteert een nieuwe eindige verzameling.
3- Een subset van een eindige set is eindig en de kardinaliteit is kleiner dan of gelijk aan die van de originele set.
4- De lege set is een eindige set.
Voorbeelden
Er zijn veel voorbeelden van eindige verzamelingen. Enkele voorbeelden zijn:
Set M. van de maanden van het jaar, die in uitgebreide vorm als volgt kunnen worden geschreven:
M. = Januari, februari, maart, april, mei, juni, juli, augustus, september, oktober, november, december, de kardinaliteit van M is 12.
Set S van de dagen van de week: S = Maandag, dinsdag, woensdag, donderdag, vrijdag, zaterdag, zondag. De kardinaliteit van S is 7.
Set Ñ van de letters van het Spaanse alfabet is een eindige set, deze set bij extensie is als volgt geschreven:
Ñ = a, b, c, d, e, f, g, h, ik, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z en de kardinaliteit is 27.
Set V. van de klinkers in het Spaans is een subset van de verzameling Ñ:
V. Ñ daarom is het een eindige verzameling.
De eindige reeks V. in uitgebreide vorm is het als volgt geschreven: V. = a, e, i, o, u en de kardinaliteit is 5.
Sets kunnen worden uitgedrukt door begrip. Set F. bestaande uit de letters van het woord "eindig" is een voorbeeld:
F. = x / x is een letter van het woord "eindig"
Genoemde reeks op een uitgebreide manier uitgedrukt zal zijn:
F. = f, i, n, t, o waarvan de kardinaliteit 5 is en daarom een eindige verzameling is.
Meer voorbeelden
De kleuren van de regenboog is een ander voorbeeld van een eindige verzameling, de verzameling C van deze kleuren is:
C = rood, oranje, geel, groen, cyaan, blauw, violet en de kardinaliteit is 7.
De reeks fasen F. de la Luna is een ander voorbeeld van een eindige verzameling:
F. = Nieuwe maan, eerste kwartaal, volle maan, laatste kwartaal deze set heeft kardinaliteit 4.
Een andere eindige reeks is die gevormd door de planeten van het zonnestelsel:
P = Mercurius, Venus, Aarde, Mars, Jupiter, Saturnus, Uranus, Neptunus, Pluto van kardinaliteit 9.
Opgeloste oefeningen
Oefening 1
De volgende set A = x∊ R / x ^ 3 = 27 wordt gegeven. Druk het in woorden uit en schrijf het in extensie, geef de kardinaliteit aan en zeg of het al dan niet eindig is.
Oplossing: De verzameling A is de verzameling reële getallen x zodanig dat x in blokjes wordt gebracht als resultaat 27.
De vergelijking x ^ 3 = 27 heeft drie oplossingen: ze zijn x1 = 3, x2 = (-3/2 + 3√3 / 2 i) en x3 = (-3/2 - 3√3 / 2 i). Van de drie oplossingen is alleen x1 reëel, terwijl de andere twee complexe getallen zijn.
Omdat de definitie van de set A zegt dat x tot de reële getallen behoort, maken de oplossingen in de complexe getallen geen deel uit van de set A.
De set A uitgebreid uitgedrukt is:
A = 3, wat een eindige reeks kardinaliteit 1 is.
Oefening 2
Schrijf in symbolische vorm (door begrip) en in uitgebreide vorm de verzameling B van reële getallen die groter zijn dan 0 (nul) en kleiner dan of gelijk aan 0 (nul). Geef de kardinaliteit aan en of het al dan niet eindig is.
Oplossing: B = x∊ R / 0 < x <= 0
De verzameling B is leeg omdat een reëel getal x niet tegelijkertijd groter en kleiner kan zijn dan nul, net zoals het niet 0 en ook kleiner dan 0 kan zijn.
B = en zijn kardinaliteit is 0. De lege verzameling is een eindige verzameling.
Oefening 3
De verzameling S van de oplossingen van een bepaalde vergelijking wordt gegeven. De verzameling S door begrip is als volgt geschreven:
S = x∊ R / (x-3) (x ^ 2 - 9x + 20) = 0
Schrijf de genoemde verzameling in uitgebreide vorm, geef de kardinaliteit ervan aan en geef aan of het een eindige verzameling is of niet.
Oplossing: In de eerste plaats, bij het analyseren van de uitdrukking die de verzameling S beschrijft, wordt verkregen dat het een verzameling reële x-waarden is die oplossingen zijn van de vergelijking:
(x-3) (x ^ 2 - 9x + 20) = 0 (*)
Een oplossing van deze vergelijking is x = 3, wat een reëel getal is en daarom tot S. behoort.Maar er zijn meer oplossingen die kunnen worden verkregen door te zoeken naar de oplossingen van de kwadratische vergelijking:
(x ^ 2 - 9x + 20) = 0
De bovenstaande uitdrukking kan als volgt worden verwerkt:
(x - 4) (x - 5) = 0
Dat leidt ons naar nog twee oplossingen van de oorspronkelijke vergelijking (*) die x = 4 en x = 5 zijn. Kortom, de vergelijking (*) heeft als oplossingen 3, 4 en 5.
De set S uitgedrukt in uitgebreide vorm ziet er als volgt uit:
S = 3, 4, 5, die kardinaliteit 3 heeft en daarom een eindige verzameling is.
Oefening 4
Er zijn twee sets A = 1, 5, 7, 9, 11 en B = x ∊ N / x is even ^ x < 10 .
Schrijf expliciet de set B en zoek de vereniging met de set A. Zoek ook het snijpunt van deze twee sets en sluit af.
Oplossing: set B is opgebouwd uit natuurlijke getallen zodat ze even zijn en ook kleiner zijn dan de waarde 10, daarom wordt set B in uitgebreide vorm als volgt geschreven:
B = 2, 4, 6, 8
De vereniging van set A met set B is:
EEN U B = 1, 2, 4, 5, 6, 7, 8, 9, 11
en het snijpunt van set A met set B wordt als volgt geschreven:
A ⋂ B = = Ø is de lege set.
Opgemerkt moet worden dat de vereniging en onderschepping van deze twee eindige verzamelingen leidt tot nieuwe verzamelingen, die op hun beurt ook eindig zijn..
Referenties
- Fuentes, A. (2016). BASIS WISKUNDE. Een inleiding tot calculus. Lulu.com.
- Garo, M. (2014). Wiskunde: kwadratische vergelijkingen: hoe een kwadratische vergelijking op te lossen. Marilù Garo.
- Haeussler, E. F., en Paul, R. S. (2003). Wiskunde voor management en economie. Pearson Education.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Wiskunde 1 SEP. Drempel.
- Preciado, C. T. (2005). Wiskundecursus 3e. Redactioneel Progreso.
- Wiskunde 10 (2018). "Voorbeelden van eindige sets". Hersteld van: matematicas10.net
- Rock, N. M. (2006). Algebra I is gemakkelijk! Zo makkelijk. Team Rock Press.
- Sullivan, J. (2006). Algebra en trigonometrie. Pearson Education.
- Wikipedia. Eindige reeks. Hersteld van: es.wikipedia.com

Niemand heeft nog op dit artikel gereageerd.