De sferische coördinaten zijn een puntlocatiesysteem in een driedimensionale ruimte bestaande uit een radiale coördinaat en twee hoekcoördinaten genaamd poolcoördinaat en azimutcoördinaat.
Figuur 1, die we hieronder zien, toont de sferische coördinaten (r, θ, φ) van een punt M. Deze coördinaten worden verwezen naar een orthogonaal systeem van Cartesische assen X, Y, Z van oorsprong O.
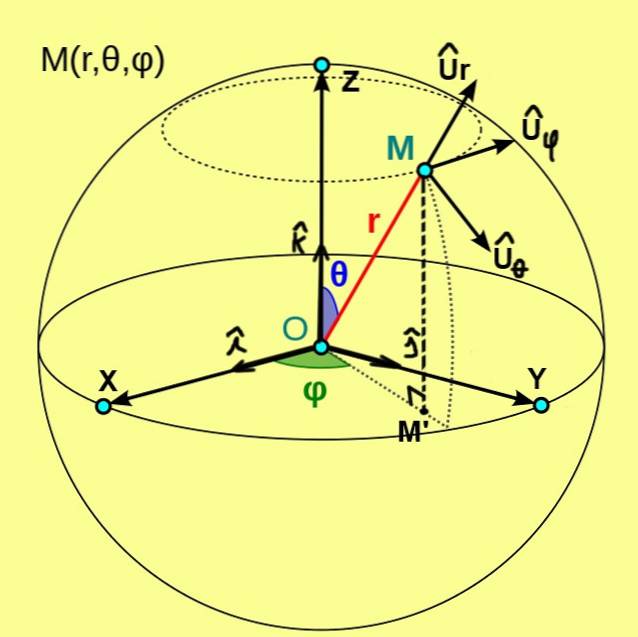
In dit geval is de coördinaat r van punt M de afstand van dat punt tot de oorsprong O. De poolcoördinaat θ vertegenwoordigt de hoek tussen de positieve halve as Z en de straalvector OM. Terwijl de azimutale coördinaat φ de hoek is tussen de positieve halve as X en de straalvector OM ', waarbij M' de orthogonale projectie is van M op het XY-vlak.
De radiale coördinaat r neemt alleen positieve waarden aan, maar als een punt zich bij de oorsprong bevindt, is r = 0. De poolcoördinaat θ neemt als minimumwaarde 0º voor punten op de positieve Z-halve as en een maximumwaarde 180º voor de punten bevindt zich op de negatieve Z-halve as. Ten slotte neemt de azimutale coördinaat φ als minimumwaarde 0º en een maximale hoogte van 360º.
0 ≤ r < ∞
0 ≤ θ ≤ 180º
0 ≤ φ < 360º
Artikel index
De formules waarmee de cartesiaanse coördinaten (x, y, z) van een punt M kunnen worden verkregen, worden hieronder gegeven, uitgaande van de sferische coördinaten van hetzelfde (r, θ, φ) punt bekend zijn:
x = r Sen (θ) Cos (φ)
y = r Sen (θ) Sen (φ)
z = r Cos (θ)
Op dezelfde manier is het nuttig om de relaties te vinden die van de cartesiaanse coördinaten (x, y, z) van een bepaald punt naar de bolcoördinaten van dat punt gaan:
r = √ (x ^ 2 + y ^ 2 + z ^ 2)
θ = Arctan (√ (x ^ 2 + y ^ 2) / z)
φ = Arctan (y / x)
Uit de sferische coördinaten wordt een orthonormale basis van basisvectoren gedefinieerd, die worden aangeduid met Ur, Uθ, Uφ. Figuur 1 toont deze drie eenheidsvectoren, die de volgende kenmerken hebben:
- Ur is de eenheidsvector die raakt aan de radiale lijn θ = ctte en φ = ctte;
- Uθ is de eenheidsvector die raakt aan de boog φ = ctte en r = ctte;
- Uφ is de eenheidsvector die raakt aan de boog r = ctte en θ = ctte.
De positievector van een punt in de ruimte in sferische coördinaten wordt als volgt geschreven:
r = r Ur
Maar een oneindig kleine variatie of verplaatsing van een punt in de driedimensionale ruimte, in deze coördinaten, wordt uitgedrukt door de volgende vectorrelatie:
dr = dr Ur + r dθ Uθ + r Sen (θ) dφ Uφ
Ten slotte wordt een oneindig klein volume dV in sferische coördinaten als volgt geschreven:
dV = r ^ 2 Sen (θ) dr dθ dφ
Deze relaties zijn erg handig voor het berekenen van lijn- en volume-integralen in fysieke situaties met sferische symmetrie..
Onder geografische coördinaten wordt verstaan de coördinaten die dienen om plaatsen op het aardoppervlak te lokaliseren. Dit systeem gebruikt de coördinaten van de lengte- en breedtegraad om de positie op het aardoppervlak te bepalen..
In het geografische coördinatensysteem wordt aangenomen dat het aardoppervlak bolvormig is met straal Rt, hoewel bekend is dat het aan de polen is afgevlakt, en een reeks denkbeeldige lijnen die parallellen en meridianen worden genoemd, wordt beschouwd.
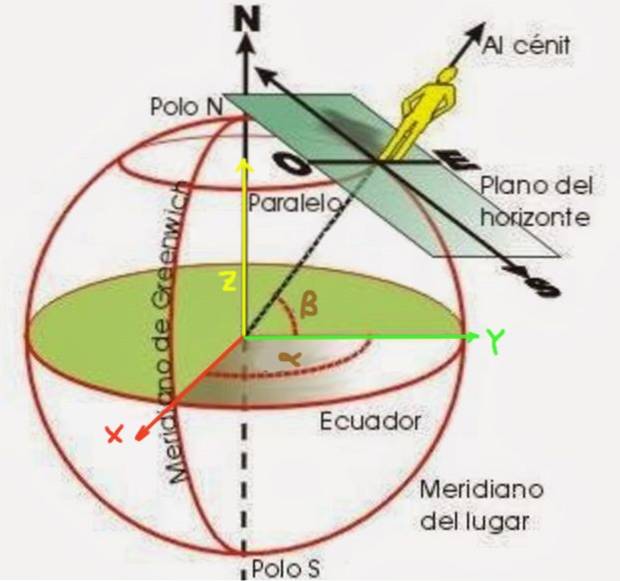
De breedtegraad β is een hoek gevormd door een straal die begint vanaf het middelpunt van de aarde tot het punt dat u wilt positioneren. Het wordt gemeten vanaf het equatoriale vlak, zoals weergegeven in figuur 2. Aan de andere kant is de lengtegraad α de hoek die de meridiaan van het punt dat zich bevindt vormt ten opzichte van de nulmeridiaan (bekend als de meridiaan van Greenwich)..
De breedtegraad kan noord- of zuiderbreedte zijn, afhankelijk van of de plaats die u zoekt zich op het noordelijk halfrond of op het zuidelijk halfrond bevindt. Evenzo kan de lengtegraad west of oost zijn, afhankelijk van of de locatie ten westen of oosten van de nulmeridiaan ligt..
Om deze formules te verkrijgen, is het eerste dat u moet instellen een coördinatensysteem. Het XY-vlak wordt zo gekozen dat het samenvalt met het equatoriale vlak, waarbij de positieve X-halve as degene is die vanuit het centrum van de aarde gaat en door de nulmeridiaan gaat. Op zijn beurt passeert de Y-as de meridiaan van 90º E. Het aardoppervlak heeft een straal Rt.
Met dit coördinatensysteem zien de transformaties van geografisch naar bolvormig er als volgt uit:
αEβN → (Rt, θ = 90º-β, φ = α)
αOβN → (Rt, θ = 90º-β, φ = 360º-α)
αEβS → (Rt, θ = 90º + β, φ = α)
αOβS → (Rt, θ = 90º + β, φ = 360º-α)
De geografische coördinaten van Palma de Mallorca (Spanje) zijn:
Oosterlengte 38.847º en noorderbreedte 39.570º. Om de sferische coördinaten te bepalen die overeenkomen met Palma de Mallorca, wordt de eerste van de formules van de formules in de vorige sectie toegepast:
38.847ºE39.570ºN → (r = 6371 km, θ = 90º-39.570º, φ = 38.847º)
Dus de sferische coördinaten zijn:
Palma de Mallorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)
In het vorige antwoord hebben we r gelijk genomen aan de gemiddelde straal van de aarde.
Wetende dat de Falklandeilanden (Malvinas) geografische coördinaten hebben van 59ºO 51,75º ZB, bepaal dan de corresponderende poolcoördinaten. Onthoud dat de X-as van het centrum van de aarde naar de 0º meridiaan en op het equatoriale vlak gaat; de Y-as ook in het equatoriale vlak en door de meridiaan van 90º West; tenslotte de Z-as op de rotatie-as van de aarde in de richting zuid-noord.
Om de bijbehorende bolcoördinaten te vinden, gebruiken we de formules die in de vorige sectie zijn gepresenteerd:
59ºO 51.75ºS → (r = 6371 km, θ = 90º + 51.75º, φ = 360º-59º) dat wil zeggen
Falklands: (r = 6371 km, θ = 141,75º, φ = 301º)
Zoek de cartesiaanse coördinaten van Palma de Mallorca in het XYZ cartesiaanse referentiesysteem in figuur 2.
Oplossing: Eerder, in voorbeeld 1, werden de sferische coördinaten verkregen uitgaande van de geografische coördinaten van Palma de Mallorca. De hierboven gepresenteerde formules kunnen dus worden gebruikt om van bolvormig naar cartesiaans te gaan:
x = 6371 km Sen (50.43º) Cos (38.85º)
y = 6371 km Sen (50.43º) Sen (38.85º)
z = 6371 km Cos (50.43º)
Bij het uitvoeren van de bijbehorende berekeningen hebben we:
Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)
Zoek de cartesiaanse coördinaten van de Falklandeilanden in het XYZ cartesiaanse referentiesysteem in figuur 2.
Oplossing: Eerder, in voorbeeld 2, werden de sferische coördinaten verkregen uitgaande van de geografische coördinaten van de Falklandeilanden. De hierboven gepresenteerde formules kunnen dus worden gebruikt om van bolvormig naar cartesiaans te gaan:
x = 6371 km Sen (141.75º) Cos (301º)
y = 6371 km Sen (141.75º) Sen (301º)
z = 6371 km Cos (141,75º)
Door de bijbehorende berekeningen uit te voeren, verkrijgen we:
Falklandeilanden: (x = 2031 km, y = -3381 km, z = -5003)
Niemand heeft nog op dit artikel gereageerd.