
Vierhoekige elementen, eigenschappen, classificatie, voorbeelden
EEN vierhoek is een veelhoek met vier zijden en vier hoekpunten. Hun tegenoverliggende zijden zijn degenen die geen gemeenschappelijke hoekpunten hebben, terwijl ze dat wel zijn opeenvolgende zijden die met een gemeenschappelijk hoekpunt.
In een vierhoek zijn ze aangrenzende hoeken degenen die een kant delen, terwijl de tegenovergestelde hoeken ze hebben geen gemeenschappelijke kanten. Een ander belangrijk kenmerk van een vierhoek is dat de som van zijn vier interne hoeken is tweemaal de vlakke hoek, dat wil zeggen 360º of 2π radialen.
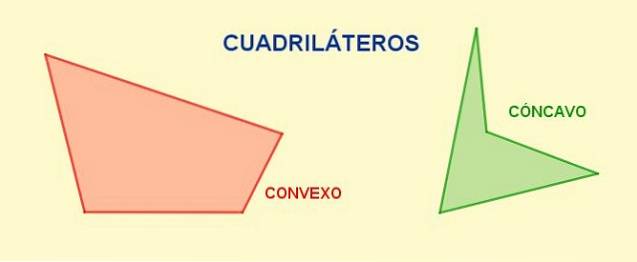
Diagonalen zijn de segmenten die een hoekpunt verbinden met zijn tegengestelde en in een bepaalde vierhoek, van elk hoekpunt kan een enkele diagonaal worden getekend. Het totale aantal diagonalen in een vierhoek is twee.
Vierhoeken zijn figuren die de mensheid al sinds de oudheid kent. De archeologische archieven, evenals de constructies die vandaag de dag overleven, getuigen hiervan..
Evenzo blijven de vierhoeken vandaag de dag een belangrijke plaats innemen in het dagelijkse leven van iedereen. De lezer kan dit formulier vinden op het scherm waarin de tekst op dit moment wordt voorgelezen, op ramen, deuren, auto-onderdelen en talloze andere plaatsen..
Artikel index
- 1 Classificatie van vierhoeken
- 1.1 Soorten parallellogram
- 2 Trapezium
- 2.1 Soorten trapezoïden
- 3 parallellogram
- 3.1 Oppervlakte van een parallellogram
- 3.2 Diagonalen van een parallellogram
- 3.3 Wet van parallellogrammen
- 4 rechthoek
- 4.1 Diagonalen van een rechthoek
- 5 vierkant
- 6 ruit
- 7 voorbeelden
- 7.1 Voorbeeld 1
- 7.2 Voorbeeld 2
- 7.3 Voorbeeld 3
- 8 Oefeningen opgelost
- 8.1 - Oefening 1
- 8.2 - Oefening 2
- 9 referenties
Vierzijdige classificatie
Volgens het parallellisme van de tegenoverliggende zijden worden de vierhoeken als volgt geclassificeerd:
- Trapezium, wanneer er geen parallellisme is en de vierhoek convex is.
- Trapeze, wanneer er parallellisme is tussen een paar tegenoverliggende zijden.
- Parallellogram, wanneer de tegenoverliggende zijden twee aan twee evenwijdig zijn.
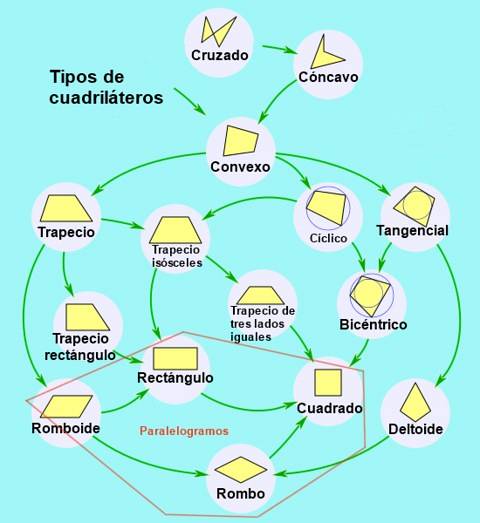
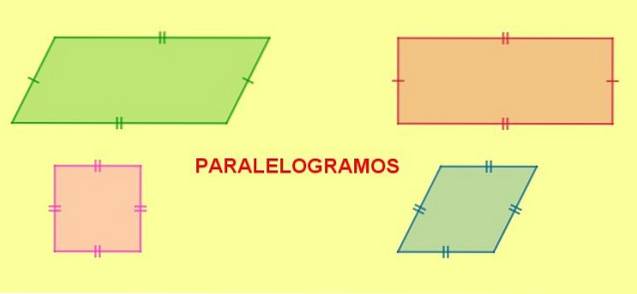
Soorten parallellogram
Parallellogrammen kunnen op hun beurt als volgt worden geclassificeerd op basis van hun hoeken en zijden:
- Rechthoek, is het parallellogram met zijn vier interne hoeken van gelijke grootte. De binnenhoeken van een rechthoek vormen een rechte hoek (90º).
- Plein, is een rechthoek waarvan de vier zijden even groot zijn.
- Diamant, is het parallellogram met zijn vier gelijke zijden, maar verschillende aangrenzende hoeken.
- Rhomboid, parallellogram met verschillende aangrenzende hoeken.
Trapeze
De trapezium is een convexe vierhoek met twee evenwijdige zijden.
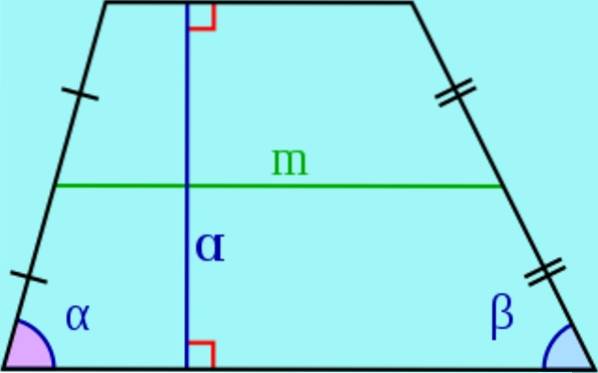
- In een trapezium worden de evenwijdige zijden genoemd bases en de niet-parallellen worden genoemd lateraal.
- De hoogte van een trapezium is de afstand tussen de twee bases, dat wil zeggen de lengte van een segment met uiteinden aan de basis en loodrecht daarop. Dit segment wordt ook wel een hoogte van de trapezium genoemd..
- De mediaan- is het segment dat de middelpunten van de zijtakken verbindt. Aangetoond kan worden dat de mediaan evenwijdig is aan de bases van de trapezium en dat de lengte gelijk is aan de halve som van de bases.
- De oppervlakte van een trapezium is de hoogte vermenigvuldigd met de halve som van de bases:
Oppervlakte van een trapezium = hoogte * (basis 1 + basis 2) / 2
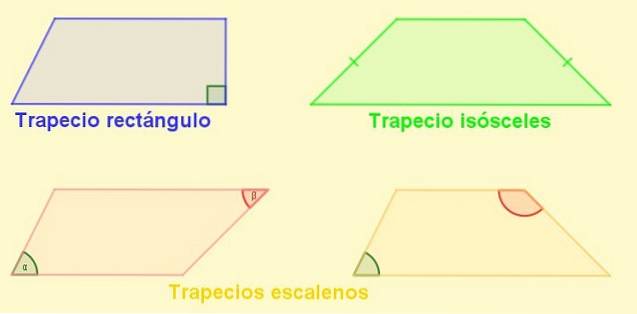
Soorten trapezoïden
-Rechthoekige trapezium: Is degene met een laterale loodrecht op de bases. Deze lateraal is ook de hoogte van het trapezium.
-Trapezium gelijkbenig: Degene met zijden van gelijke lengte. In een gelijkbenig trapezium zijn de hoeken naast de bases gelijk.
-Scalene trapezium: Degene met zijden van verschillende lengtes. De tegenovergestelde hoeken kunnen de ene acuut en de andere stomp zijn, maar het kan ook gebeuren dat beide stomp of beide acuut zijn..
Parallellogram
Het parallellogram is een vierhoek waarvan de tegenoverliggende zijden twee aan twee evenwijdig zijn. In een parallellogram zijn de tegenoverliggende hoeken gelijk en de aangrenzende hoeken zijn aanvullend, of met andere woorden, de aangrenzende hoeken zijn opgeteld 180º.
Als een parallellogram een rechte hoek heeft, dan zijn alle andere hoeken dat ook en wordt de resulterende figuur genoemd rechthoek. Maar als de rechthoek ook aangrenzende zijden van dezelfde lengte heeft, dan zijn alle zijden gelijk en is de resulterende figuur a plein.
Als een parallellogram twee aangrenzende zijden van dezelfde lengte heeft, hebben alle zijden dezelfde lengte en is de resulterende figuur een diamant.
De hoogte van een parallellogram is een segment met uiteinden aan de tegenoverliggende zijden en loodrecht daarop..
Oppervlakte van een parallellogram
De oppervlakte van een parallellogram is het product van de basis maal de hoogte, de basis is een zijde loodrecht op de hoogte (figuur 6).
Oppervlakte van een parallellogram = basis x hoogte = a. h
Diagonalen van een parallellogram
Het kwadraat van de diagonaal dat begint bij een hoekpunt is gelijk aan de som van de vierkanten van de twee zijden grenzend aan dat hoekpunt plus het dubbele product van die zijden door de cosinus van de hoek van dat hoekpunt:
F.twee = eentwee + dtwee + 2 a d Cos (α)
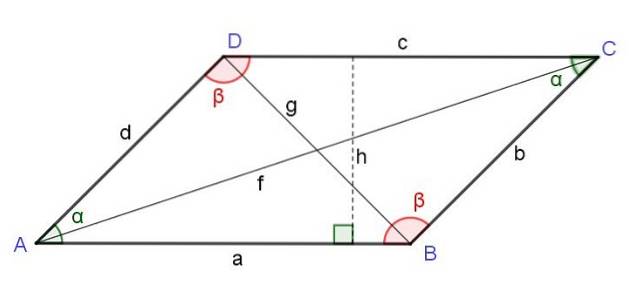
Het kwadraat van de diagonaal tegenover het hoekpunt van een parallellogram is gelijk aan de som van de kwadraten van de twee zijden naast het hoekpunt en het dubbele product van die zijden aftrekken van de cosinus van de hoek van dat hoekpunt:
gtwee = eentwee + dtwee - 2 a d Cos (α)
Wet van parallellogrammen
In elk parallellogram is de som van de vierkanten van de zijden gelijk aan de som van de vierkanten van de diagonalen:
naartwee + btwee + ctwee + dtwee = ftwee + gtwee
Opnieuwctangle
De rechthoek is een vierhoek waarvan de tegenoverliggende zijden twee aan twee evenwijdig zijn en die ook een rechte hoek heeft. Met andere woorden, de rechthoek is een soort parallellogram met een rechte hoek. Omdat het parallellogram is, de rechthoek heeft tegenoverliggende zijden van gelijke lengte a = c en b = d.
Maar zoals in elk parallellogram zijn de aangrenzende hoeken aanvullend en de tegenoverliggende hoeken gelijk, in de rechthoek omdat het een rechte hoek heeft, zal het noodzakelijkerwijs rechte hoeken vormen in de andere drie hoeken. Namelijk in een rechthoek meten alle binnenhoeken 90º of π / 2 radialen.
Diagonalen van een rechthoek
In een rechthoek zijn de diagonalen even lang, zoals hieronder zal worden aangetoond. De redenering is als volgt; Een rechthoek is een parallellogram met al zijn rechte hoeken en erft dus alle eigenschappen van het parallellogram, inclusief de formule die de lengte van de diagonalen geeft:
F.twee = eentwee+ dtwee + 2 a d Cos (α)
gtwee = eentwee + dtwee - 2 a d Cos (α)
met α = 90º
Wat Cos (90º) = 0, dan gebeurt het dat:
F.twee = gtwee = eentwee + dtwee
Dat is f = g, en dus de lengtes F. Y g van de twee diagonalen van de rechthoek zijn gelijk en hun lengte wordt gegeven door:
Diagonalen lengte van een rechthoek = √ (atwee + btwee
Ook indien in een rechthoek met aangrenzende zijden naar Y b de ene kant wordt als basis genomen, de andere kant zal de hoogte hebben en bijgevolg zal het oppervlak van de rechthoek zijn:
Oppervlakte van de rechthoek = a x b.
De omtrek is de som van alle zijden van de rechthoek, maar aangezien de tegenstellingen gelijk zijn, volgt daaruit dat voor een rechthoek met zijden naar Y b de omtrek wordt gegeven door de volgende formule:
Omtrek van de rechthoek = 2 (a + b)
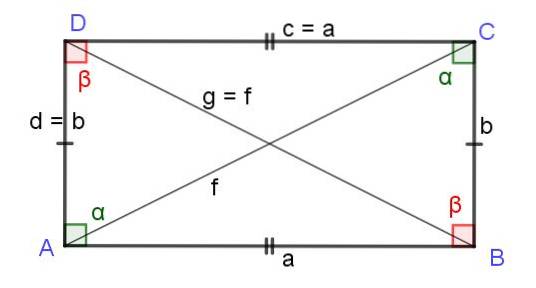
Plein
Het vierkant is een rechthoek met aangrenzende zijden van dezelfde lengte. Als het vierkant een kant heeft naar, dan zijn diagonalen F. Y g dezelfde lengte hebben, namelijk f = g = (√2) een.
De oppervlakte van een vierkant is de zijde in het kwadraat:
Oppervlakte van een vierkant = atwee
De omtrek van een vierkant is tweemaal de zijde:
Omtrek van een vierkant = 4 a
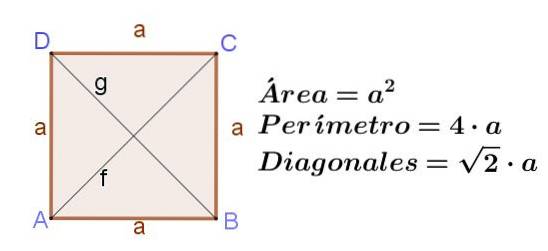
Diamant
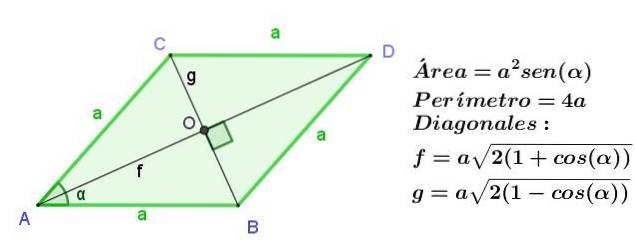
De ruit is een parallellogram met de aangrenzende zijden van dezelfde lengte, maar zoals in een parallellogram zijn de tegenoverliggende zijden gelijk, alle zijden van een ruit zijn even lang.
De diagonalen van een ruit hebben een verschillende lengte, maar snijden elkaar loodrecht.
Voorbeelden
voorbeeld 1
Laat zien dat in een vierhoek (niet gekruist) de interne hoeken samen 360 ° bedragen.
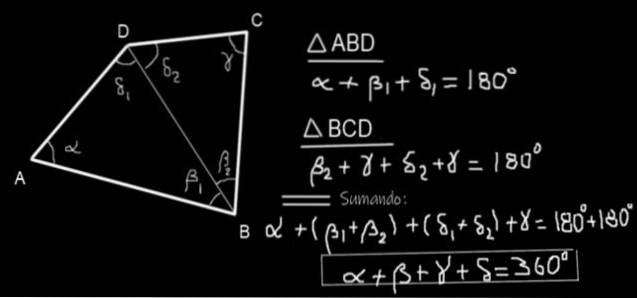
Een vierhoek ABCD wordt beschouwd (zie figuur 10) en de diagonale BD wordt getekend. Er worden twee driehoeken ABD en BCD gevormd. De som van de binnenhoeken van driehoek ABD is:
α + β1 + δ1 = 180º
En de som van de interne hoeken van driehoek BCD is:
β2 + γ + δtwee = 180º
Als we de twee vergelijkingen optellen, krijgen we:
α + β1 + δ1 + βtwee + γ + δtwee = 180º + 180º
Groepering:
α + (β1 + βtwee) + (δ1 + δtwee) + γ = 2 * 180º
Door te groeperen en te hernoemen, wordt uiteindelijk aangetoond dat:
α + β + δ + γ = 360º
Voorbeeld 2
Laat zien dat de mediaan van een trapezium evenwijdig is aan zijn bases en dat de lengte de halve som is van de bases.
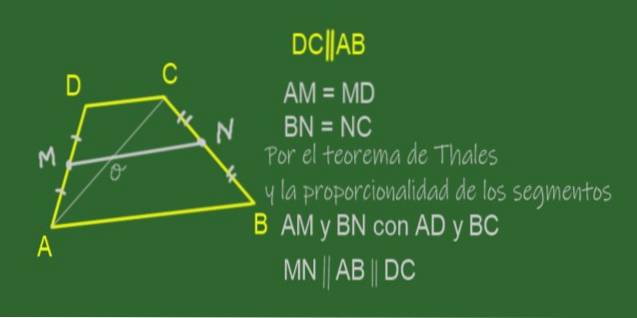
De mediaan van een trapezium is het segment dat de middelpunten van zijn zijden verbindt, dat wil zeggen de niet-parallelle zijden. In de trapezoïde ABCD getoond in figuur 11 is de mediaan MN.
Aangezien M het middelpunt van AD is en N het middelpunt van BC, is het waar dat de verhoudingen AM / AD en BN / BC gelijk zijn.
Dat wil zeggen, AM is evenredig met BN in dezelfde verhouding als AD is tot BC, dus de voorwaarden worden gegeven voor de toepassing van Thales '(wederkerige) stelling die het volgende stelt:
Als proportionele segmenten worden bepaald in drie of meer lijnen die door twee secanten zijn gesneden, dan zijn deze lijnen allemaal parallel.
In ons geval wordt geconcludeerd dat de lijnen MN, AB en DC parallel aan elkaar lopen, dus:
"Lde mediaan van een trapezium is evenwijdig aan de basis.
Nu zal de stelling van Thales worden toegepast:
Een reeks parallellen die door twee of meer secanten zijn gesneden, bepalen de proportionele segmenten.
In ons geval AD = 2 AM, AC = 2 AO, dus de driehoek DAC is vergelijkbaar met de driehoek MAO, en bijgevolg DC = 2 MO.
Een soortgelijk argument stelt ons in staat te bevestigen dat CAB vergelijkbaar is met CON, waarbij CA = 2 CO en CB = 2 CN. Hieruit volgt onmiddellijk dat AB = 2 AAN.
Kortom, AB = 2 AAN en DC = 2 MO. Dus bij het toevoegen hebben we:
AB + DC = 2 AAN + 2 MO = 2 (MO + AAN) = 2 MN
Eindelijk is MN gewist:
MN = (AB + DC) / 2
En er wordt geconcludeerd dat de mediaan van een trapezium de halve som van de bases meet, of met andere woorden: de mediaan meet de som van de bases, gedeeld door twee.
Voorbeeld 3
Laat zien dat in een ruit de diagonalen elkaar haaks snijden.

Het bord in figuur 12 toont de benodigde constructie. Eerst wordt het parallellogram ABCD getekend met AB = BC, dat wil zeggen een ruit. Diagonalen AC en DB bepalen acht hoeken die in de figuur worden weergegeven.
Met behulp van de stelling (a.i.p.) die stelt dat afwisselende binnenhoeken tussen parallellen gesneden door een secans gelijke hoeken bepalen, kunnen we het volgende vaststellen:
α1 = γ1, α2 = γ2, δ1 = Β1 en δ2 = β2.
Aan de andere kant, aangezien de aangrenzende zijden van een ruit even lang zijn, worden vier gelijkbenige driehoeken bepaald:
DAB, BCD, CDA en ABC
Nu wordt de driehoek (gelijkbenige) stelling aangeroepen, die stelt dat de hoeken grenzend aan de basis even groot zijn, waaruit wordt geconcludeerd dat:
δ1 = β2, δ2 = β1, α2 = γ1 en α1 = γ2 (**)
Als de relaties (*) en (**) worden gecombineerd, wordt de volgende hoekgelijkheid bereikt:
α1 = α2 = γ1 = γ1 enerzijds en β1 = Β2 = δ1 = δ2 aan de andere kant.
Herinnerend aan de stelling van gelijke driehoeken die stelt dat twee driehoeken met een gelijke zijde tussen twee gelijke hoeken gelijk zijn, hebben we:
AOD = AOB en dus ook de hoeken ∡AOD = ∡AOB.
Dan ∡AOD + ∡AOB = 180º, maar aangezien beide hoeken even groot zijn, hebben we 2 ∡AOD = 180º wat impliceert dat ∡AOD = 90º.
Dat wil zeggen, het wordt geometrisch weergegeven dat de diagonalen van een ruit elkaar loodrecht snijden.
Oefeningen opgelost
- Oefening 1
Laat zien dat bij een rechter trapezium de niet-rechte hoeken aanvullend zijn.
Oplossing
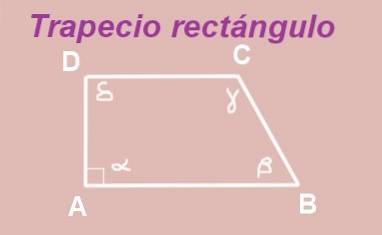
De trapeziumvormige ABCD is geconstrueerd met basen AB en DC parallel. De binnenhoek van hoekpunt A is goed (het meet 90º), dus we hebben een rechter trapezium.
Hoeken α en δ zijn interne hoeken tussen twee parallellen AB en DC, daarom zijn ze gelijk, dat wil zeggen δ = α = 90º.
Aan de andere kant is aangetoond dat de som van de interne hoeken van een vierhoek oploopt tot 360 °, dat wil zeggen:
α + β + γ + δ = 90º + β + 90º + δ = 360º.
Het bovenstaande leidt tot:
β + δ = 180º
Bevestigend wat men wilde aantonen, dat de hoeken β en δ aanvullend zijn.
- Oefening 2
Een parallellogram ABCD heeft AB = 2 cm en AD = 1 cm, daarnaast is de hoek BAD 30º. Bepaal de oppervlakte van genoemd parallellogram en de lengte van zijn twee diagonalen.
Oplossing
De oppervlakte van een parallellogram is het product van de lengte van de basis maal de hoogte. In dit geval wordt de lengte van het segment b = AB = 2 cm als basis genomen, de andere zijde heeft lengte a = AD = 1 cm en wordt de hoogte h als volgt berekend:
h = AD * Sen (30º) = 1 cm * (1/2) = ½ cm.
Dus: Oppervlakte = b * h = 2 cm * ½ cm = 1 cmtwee.
Referenties
- C. E. A. (2003). Geometrie-elementen: met oefeningen en geometrie van het kompas. Universiteit van Medellin.
- Campos, F., Cerecedo, F. J. (2014). Wiskunde 2. Grupo Redactie Patria.
- Freed, K. (2007). Ontdek Polygonen. Benchmark Onderwijsbedrijf.
- Hendrik, V. (2013). Gegeneraliseerde polygonen. Birkhäuser.
- IGER. (s.f.). Wiskunde eerste semester Tacaná. IGER.
- Jr. geometrie. (2014). Veelhoeken. Lulu Press, Inc.
- Miller, Heeren en Hornsby. (2006). Wiskunde: redeneren en toepassingen (tiende editie). Pearson Education.
- Patiño, M. (2006). Wiskunde 5. Redactioneel Progreso.
- Wikipedia. Vierhoeken. Hersteld van: es.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.