
Opeenvolgende derivaten (met opgeloste oefeningen)
De opeenvolgende afgeleiden zijn de afgeleiden van een functie na de tweede afgeleide. Het proces om de opeenvolgende afgeleiden te berekenen is als volgt: we hebben een functie f, die we kunnen afleiden en zo de afgeleide functie f 'verkrijgen. We kunnen deze afgeleide van f weer afleiden en krijgen (f ')'.
Deze nieuwe functie wordt de tweede afgeleide genoemd; alle afgeleiden berekend vanaf de tweede zijn opeenvolgend; Deze, ook wel hogere orde genoemd, hebben geweldige toepassingen, zoals het geven van informatie over de plot van de grafiek van een functie, het testen van de tweede afgeleide op relatieve extremen en het bepalen van oneindige reeksen..

Artikel index
- 1 Definitie
- 1.1 Voorbeeld 1
- 1.2 Voorbeeld 2
- 2 Snelheid en acceleratie
- 2.1 Voorbeeld 1
- 2.2 Voorbeeld 2
- 3 Toepassingen
- 3.1 Impliciete afleiding
- 3.2 Voorbeeld
- 3.3 Relatieve extremen
- 3.4 Voorbeeld
- 3.5 Taylor-serie
- 3.6 Voorbeeld
- 4 referenties
Definitie
Als we de notatie van Leibniz gebruiken, hebben we dat de afgeleide van een functie "y" met betrekking tot "x" dy / dx is. Om de tweede afgeleide van "y" uit te drukken met de notatie van Leibniz, schrijven we als volgt:

In het algemeen kunnen we opeenvolgende afgeleiden als volgt uitdrukken met de notatie van Leibniz, waarbij n de volgorde van de afgeleide voorstelt.

Andere gebruikte notaties zijn de volgende:
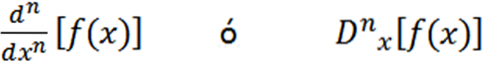
Enkele voorbeelden waar we de verschillende notaties kunnen zien zijn:
voorbeeld 1
Verkrijg alle afgeleiden van de functie f gedefinieerd door:
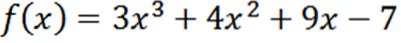
Met behulp van de gebruikelijke afleidingstechnieken hebben we dat de afgeleide van f is:

Door het proces te herhalen, kunnen we de tweede afgeleide, de derde afgeleide enzovoort verkrijgen.
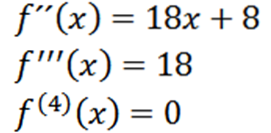
Merk op dat de vierde afgeleide nul is en de afgeleide van nul nul is, dus we hebben:

Voorbeeld 2
Bereken de vierde afgeleide van de volgende functie:
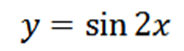
Afleiden van de gegeven functie hebben we als resultaat:
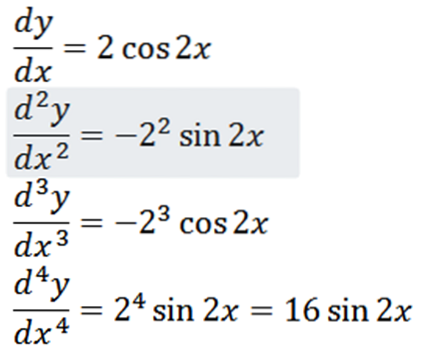
Snelheid en acceleratie
Een van de motivaties die tot de ontdekking van het derivaat hebben geleid, was de zoektocht naar de definitie van instantane snelheid. De formele definitie is als volgt:
Laat y = f (t) een functie zijn waarvan de grafiek het traject van een deeltje op een bepaald moment beschrijft t, dan is zijn snelheid op een moment t gegeven door:

Zodra de snelheid van een deeltje is verkregen, kunnen we de onmiddellijke versnelling berekenen, die als volgt wordt gedefinieerd:
De momentane versnelling van een deeltje waarvan het pad wordt gegeven door y = f (t) is:

voorbeeld 1
Een deeltje beweegt langs een lijn volgens de positiefunctie:

Waarbij "y" wordt gemeten in meters en "t" in seconden.
- Op welk moment is zijn snelheid 0?
- Op welk moment is de versnelling 0?
Bij het afleiden van de positie "y" -functie hebben we dat de snelheid en versnelling respectievelijk worden gegeven door:

Om de eerste vraag te beantwoorden, is het voldoende om te bepalen wanneer de functie v nul wordt; dit is:
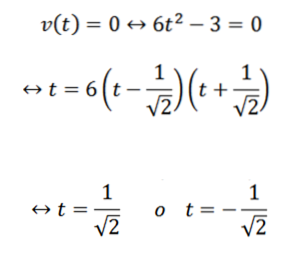
We gaan op een analoge manier verder met de volgende vraag:

Voorbeeld 2
Een deeltje beweegt langs een lijn volgens de volgende bewegingsvergelijking:

Bepaal "t, y" en "v" wanneer a = 0.
Wetende dat snelheid en acceleratie worden gegeven door

We gaan verder met het afleiden en verkrijgen van:

Als we a = 0 maken, hebben we:
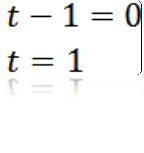
Waaruit we kunnen afleiden dat de waarde van t zodat a gelijk is aan nul t = 1 is.
Als we vervolgens de positiefunctie en de snelheidsfunctie op t = 1 evalueren, hebben we:

Toepassingen
Expliciete afleiding
Opeenvolgende derivaten kunnen ook worden verkregen door impliciete afleiding.
Voorbeeld
Zoek "y" met de volgende ellips:

Impliciet afgeleid met betrekking tot x, hebben we:
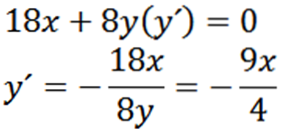
Dan geeft het impliciet opnieuw afleiden met betrekking tot x ons:

Eindelijk hebben we:
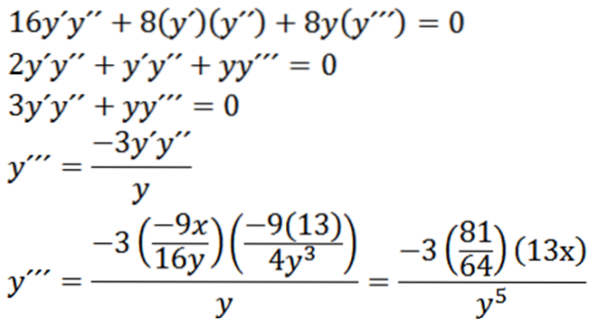
Relatieve extremen
Een ander gebruik dat we aan de afgeleiden van tweede orde kunnen geven, is bij de berekening van relatieve extremen van een functie.
Het criterium van de eerste afgeleide voor lokale extremen vertelt ons dat, als we een continue functie f hebben in een interval (a, b) en er bestaat een c die bij dat interval hoort, zodat f 'verdwijnt in c (dat wil zeggen dat c is een kritiek punt), kan zich een van de drie gevallen voordoen:
- Als f '(x)> 0 voor elke x behorende tot (a, c) en f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
- Als f '(x) < 0 para cualquier x perteneciente a (a,c) y f'(x)>0 voor x behorend tot (c, b), dan is f (c) een lokaal minimum.
- Als f '(x) hetzelfde teken heeft in (a, c) en in (c, b), impliceert dit dat f (c) geen lokaal uiterste is.
Met behulp van het criterium van de tweede afgeleide kunnen we weten of een kritiek getal van een functie een lokaal maximum of een minimum is, zonder te hoeven zien wat het teken van de functie is in de bovengenoemde intervallen..
Het tweede driftcriterium vertelt ons dat als f '(c) = 0 en dat f "(x) continu is in (a, b), het gebeurt dat als f" (c)> 0, f (c) een lokale minimum en als f "(c) < 0 entonces f(c) es un máximo local.
Als f "(c) = 0, kunnen we niets concluderen.
Voorbeeld
Gegeven de functie f (x) = x4 + (4/3) x3 - 4xtwee, vind de relatieve maxima en minima van f door het tweede afgeleide criterium toe te passen.
Eerst berekenen we f '(x) en f "(x) en we hebben:
f '(x) = 4x3 + 4xtwee - 8x
f "(x) = 12xtwee + 8x - 8
Nu, f '(x) = 0 als, en alleen als 4x (x + 2) (x - 1) = 0, en dit gebeurt als x = 0, x = 1 of x = - 2.
Om te bepalen of de verkregen kritische getallen relatieve extremen zijn, is het voldoende om bij f "te evalueren en dus het teken ervan te observeren.
f "(0) = - 8, dus f (0) is een lokaal maximum.
f "(1) = 12, dus f (1) is een lokaal minimum.
f "(- 2) = 24, dus f (- 2) is een lokaal minimum.
Taylor-serie
Laat f een functie zijn die als volgt is gedefinieerd:
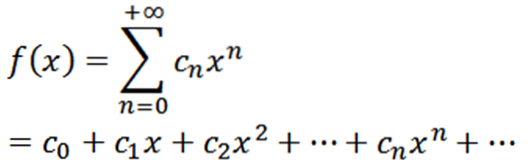
Deze functie heeft een convergentiestraal R> 0 en heeft afgeleiden van alle ordes in (-R, R). De opeenvolgende afgeleiden van f geven ons:
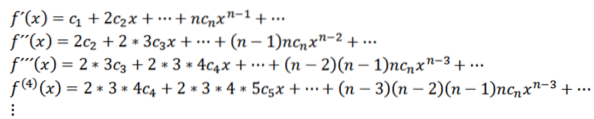
Als we x = 0 nemen, kunnen we de waarden van c verkrijgenn op basis van zijn derivaten als volgt:
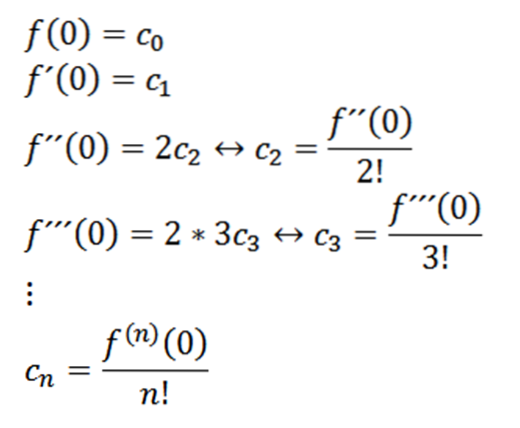
Als we n = 0 nemen als de functie f (dat wil zeggen, f ^ 0 = f), dan kunnen we de functie als volgt herschrijven:
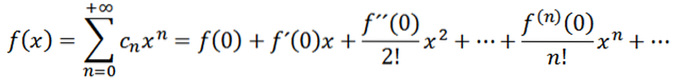
Laten we nu de functie beschouwen als een reeks machten bij x = a:
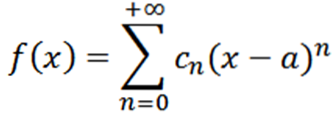
Als we een analyse uitvoeren analoog aan de vorige, zouden we hebben dat we de functie f kunnen schrijven als:
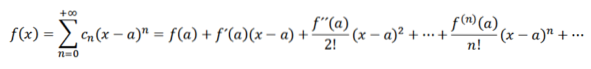
Deze series staan bekend als Taylor-series van f tot a. Als a = 0 hebben we het specifieke geval dat de Maclaurin-serie wordt genoemd. Dit type reeksen is van groot wiskundig belang, vooral bij numerieke analyse, omdat we hierdoor functies kunnen definiëren in computers zoals eX , sin (x) en cos (x).
Voorbeeld
Koop de Maclaurin-serie voor eX.
Merk op dat als f (x) = eX, dan f(n)(x) = eX en f(n)(0) = 1, dus uw Maclaurin-serie is:
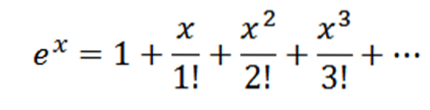
Referenties
- Frank Ayres, J., & Mendelson, E. (s.f.). Berekening 5ed. Mc Graw Hill.
- Leithold, L. (1992). De berekening met analytische meetkunde. HARLA, S.A.
- Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Berekening. Mexico: Pearson Education.
- Saenz, J. (2005). Diferentiële calculus. Hypotenusa.
- Saenz, J. (s.f.). Integrale calculus. Hypotenusa.



Niemand heeft nog op dit artikel gereageerd.