
Demonstratie van driehoeksongelijkheid, voorbeelden, opgeloste oefeningen
Het heet Driehoeksongelijkheid op de eigenschap van twee reële getallen die erin bestaan dat de absolute waarde van hun som altijd kleiner is dan of gelijk is aan de som van hun absolute waarden. Deze eigenschap wordt ook wel Minkowski-ongelijkheid of driehoeksongelijkheid genoemd.
Deze eigenschap van getallen wordt driehoeksongelijkheid genoemd omdat het bij driehoeken voorkomt dat de lengte van één zijde altijd kleiner of gelijk is aan de som van de andere twee, ook al geldt deze ongelijkheid niet altijd op het gebied van driehoeken..

Er zijn verschillende bewijzen van de driehoekige ongelijkheid in reële getallen, maar in dit geval zullen we er een kiezen op basis van de eigenschappen van absolute waarde en het binominale kwadraat.
Stelling: Voor elk paar cijfers naar Y b met betrekking tot de reële getallen moet het:
a + b | | naar |b |
Artikel index
- 1 demo
- 2 voorbeelden
- 2.1 Voorbeeld 1
- 2.2 Voorbeeld 2
- 2.3 Voorbeeld 3
- 2.4 Voorbeeld 4
- 2.5 Voorbeeld 5
- 2.6 Voorbeeld 6
- 3 Opgeloste oefeningen
- 3.1 Oefening 1
- 3.2 Oefening 2
- 3.3 Oefening 3
- 3.4 Oefening 4
- 4 referenties
Demonstratie
We beginnen met het eerste lid van de ongelijkheid te beschouwen, dat zal worden gekwadrateerd:
a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (vergelijking 1)
In de vorige stap hebben we de eigenschap gebruikt dat elk getal in het kwadraat gelijk is aan de absolute waarde van dat getal in het kwadraat, dat wil zeggen: | x | ^ 2 = x ^ 2. Ook is gebruik gemaakt van de ontwikkeling van de kwadraat binominaal.
Alle nummers X is kleiner dan of gelijk aan de absolute waarde. Als het getal positief is, is het gelijk, maar als het getal negatief is, is het altijd kleiner dan een positief getal. In dit geval zijn eigen absolute waarde, dat wil zeggen dat kan worden gesteld dat x ≤ | x |.
Het product (een b) is een getal, daarom geldt dat (een b) ≤ | een b |. Wanneer deze eigenschap wordt toegepast op (vergelijking 1), hebben we:
a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | een b | + b ^ 2 (vergelijking 2)
Overwegende dat een b | = | een || b | (Vgl. 2) kan als volgt worden geschreven:
a + b | ^ 2 ≤ a ^ 2 + 2 | een || b | + b ^ 2 (vergelijking 3)
Maar aangezien we eerder zeiden dat het kwadraat van een getal gelijk is aan de absolute waarde van het kwadraat, kan vergelijking 3 als volgt worden herschreven:
a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | b | + | b | ^ 2 (vergelijking 4)
In het tweede lid van de ongelijkheid wordt een opmerkelijk product herkend, dat bij toepassing leidt tot:
a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (vergelijking 5)
In de vorige uitdrukking moet worden opgemerkt dat de waarden die in beide leden van de ongelijkheid moeten worden gekwadrateerd positief zijn, daarom moet er ook aan worden voldaan dat:
a + b | ≤ (| a | + | b |) (vergelijking 6)
De bovenstaande uitdrukking is precies wat we wilden demonstreren.
Voorbeelden
Vervolgens zullen we de driehoekige ongelijkheid bekijken met verschillende voorbeelden.
voorbeeld 1
We nemen de waarde a = 2 en de waarde b = 5, dat wil zeggen, beide positieve getallen en we kijken of aan de ongelijkheid is voldaan of niet.
2 + 5 | ≤ | 2 | + | 5 |
7 | ≤ | 2 | + | 5 |
7 ≤ 2+ 5
Gelijkheid is geverifieerd, daarom is aan de stelling van de driehoeksongelijkheid voldaan.
Voorbeeld 2
De volgende waarden worden gekozen a = 2 en b = -5, dat wil zeggen een positief getal en het andere negatief, we controleren of aan de ongelijkheid is voldaan of niet.
2 - 5 | ≤ | 2 | + | -5 |
-3 | ≤ | 2 | + | -5 |
3 ≤ 2 + 5
Aan de ongelijkheid is voldaan, daarom is de driehoekige ongelijkheidsstelling geverifieerd.
Voorbeeld 3
We nemen de waarde a = -2 en de waarde b = 5, dat wil zeggen een negatief getal en het andere positief, we controleren of aan de ongelijkheid is voldaan of niet.
-2 + 5 | ≤ | -2 | + | 5 |
3 | ≤ | -2 | + | 5 |
3 ≤ 2 + 5
De ongelijkheid is geverifieerd, daarom is aan de stelling voldaan.
Voorbeeld 4
De volgende waarden worden gekozen a = -2 en b = -5, dat wil zeggen, beide negatieve getallen en we controleren of aan de ongelijkheid is voldaan of niet.
-2 - 5 | ≤ | -2 | + | -5 |
-7 | ≤ | -2 | + | -5 |
7 ≤ 2+ 5
Gelijkheid is geverifieerd, daarom is aan de ongelijkheidsstelling van Minkowski voldaan.
Voorbeeld 5
We nemen de waarde a = 0 en de waarde b = 5, dat wil zeggen een getal nul en het andere positief, dan kijken we of aan de ongelijkheid is voldaan of niet.
0 + 5 | ≤ | 0 | + | 5 |
5 | ≤ | 0 | + | 5 |
5 ≤ 0+ 5
Gelijkheid is vervuld, daarom is de stelling van de driehoeksongelijkheid geverifieerd.
Voorbeeld 6
We nemen de waarde a = 0 en de waarde b = -7, dat wil zeggen een getal nul en het andere positief, dan kijken we of aan de ongelijkheid is voldaan of niet.
0 - 7 | ≤ | 0 | + | -7 |
-7 | ≤ | 0 | + | -7 |
7 ≤ 0+ 7
Gelijkheid is geverifieerd, daarom is aan de driehoeksongelijkheidsstelling voldaan.
Opgeloste oefeningen
Geef in de volgende oefeningen geometrisch de driehoeksongelijkheid of Minkowski-ongelijkheid weer voor de getallen a en b.
Het getal a wordt weergegeven als een segment op de X-as, de oorsprong O valt samen met de nul van de X-as en het andere uiteinde van het segment (op punt P) bevindt zich in de positieve richting (naar rechts) van de X-as als a> 0, maar als a < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.
Evenzo wordt het getal b weergegeven als een segment waarvan de oorsprong op punt P ligt. Het andere uiterste, dat wil zeggen, punt Q bevindt zich rechts van P als b positief is (b> 0) en punt Q is | b | eenheden links van P als b<0.
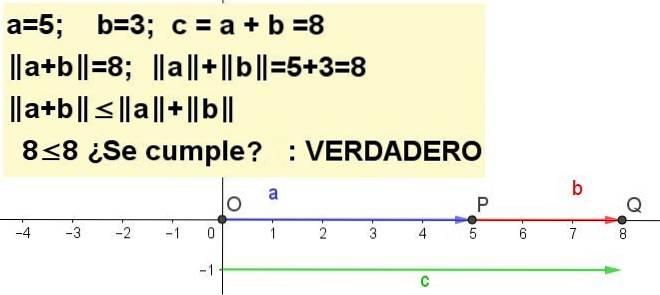
Oefening 1
Maak een grafiek van de driehoeksongelijkheid voor a = 5 en b = 3 a + b | | naar |b |, wezen c = een + b.
Oefening 2
Maak een grafiek van de driehoekige ongelijkheid voor a = 5 en b = -3.
a + b | | naar |b |, wezen c = een + b.

Oefening 3
Geef grafisch de driehoeksongelijkheid weer voor a = -5 en b = 3.
a + b | | naar |b |, wezen c = een + b.
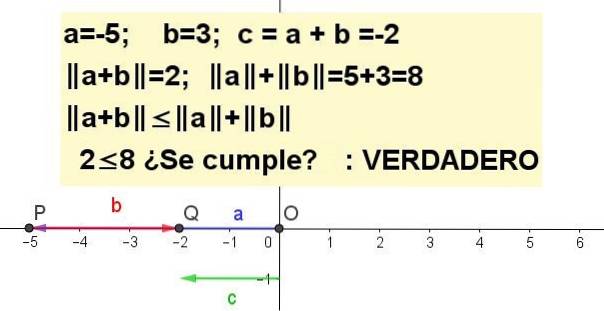
Oefening 4
Construeer grafisch de driehoekige ongelijkheid voor a = -5 en b = -3.
a + b | | naar |b |, wezen c = een + b.
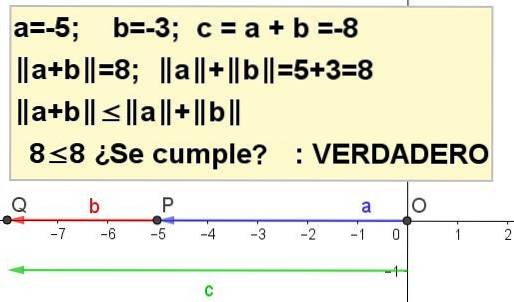
Referenties
- E. Whitesitt. (1980) Booleaanse algebra en zijn toepassingen. Redactie Continental C. A.
- Mícheál O 'Searcoid. (2003) Elementen van abstracte analyse… Afdeling wiskunde. Hogeschool Dublin, Beldfield, Dublind.
- J. Van Wyk. (2006) Wiskunde en techniek in computerwetenschappen. Instituut voor Computerwetenschappen en Technologie. Nationaal Bureau of Standards. Washington, D.C. 20234
- Eric Lehman. Wiskunde voor informatica. Google Inc.
- F. Thomson Leighton (1980). Calculus. Afdeling Wiskunde en het Computer Science and AI Laboratory, Massachusetts Institute of Technology.
- Khan Academy. Driehoeksongelijkheidsstelling. Hersteld van: khanacademy.org
- Wikipedia. Driehoekige ongelijkheid. Hersteld van: es. wikipedia.com


Niemand heeft nog op dit artikel gereageerd.