
Dynamiek van een systeem van deeltjesvoorbeelden, oefeningen
De dynamica van een deeltjessysteem Het bestaat uit de toepassing van de bewegingswetten van Newton op een reeks deeltjes, die discreet kunnen zijn (de deeltjes kunnen worden geteld) of deel uitmaken van een uitgebreid object, in dit geval is het systeem continu.
Om de beweging van een systeem van deeltjes te verklaren, is het lastig om elk afzonderlijk te analyseren en te zien welke krachten erop inwerken. In plaats daarvan wordt een representatief punt van de set gedefinieerd, genaamd de Massacentrum.
Het beschrijven van de beweging van het massamiddelpunt biedt een zeer nauwkeurig overzicht van de algehele beweging van het geheel, het maakt het ook mogelijk om de wetten van Newton toe te passen op een manier die analoog is aan wanneer het object wordt beschouwd als een dimensieloos deeltje..
Dit nieuwste model, genaamd deeltjesmodel, Het is goed voor het beschrijven van vertalingen en ook als u geen rekening hoeft te houden met de afmetingen van het object. Maar gewone objecten hebben afmetingen en als ze ook een roterende beweging hebben, moet rekening worden gehouden met de punten waarop de krachten worden uitgeoefend.
Artikel index
- 1 Voorbeelden
- 1.1 De aarde en de maan
- 1.2 Uitgebreide objecten
- 2 Het massamiddelpunt van een systeem van deeltjes
- 2.1 CM beweging
- 2.2 Forceer op CM
- 3 Oefening opgelost
- 3.1 Oplossing a
- 3.2 Oplossing b
- 3.3 Oplossing c
- 4 referenties
Voorbeelden
De aarde en de maan

Een set van discrete deeltjes m1, mtwee, m3... dat uiteindelijk beweegt met betrekking tot de oorsprong van een coördinatensysteem, vanwege een resulterende kracht die erop inwerkt, is een goed voorbeeld van een deeltjessysteem.
De aarde kan worden beschouwd als het ene deeltje en de maan als een ander, dan vormen beide een systeem van 2 deeltjes onder invloed van de zwaartekracht van de zon..
Uitgebreide objecten
Een persoon, een dier of een ander object in de omgeving kan ook worden beschouwd als een systeem van deeltjes, alleen dat deze zo klein zijn dat ze niet één voor één kunnen worden geteld. Dit is een continu systeem, maar rekening houdend met bepaalde overwegingen, is de behandeling hetzelfde als voor een discreet systeem.
Hieronder staan de details.
Het massamiddelpunt van een systeem van deeltjes
Om de studie van een deeltjessysteem te beginnen, moeten we het massamiddelpunt (CM) vinden, het punt waar alle massa van het systeem geconcentreerd is..
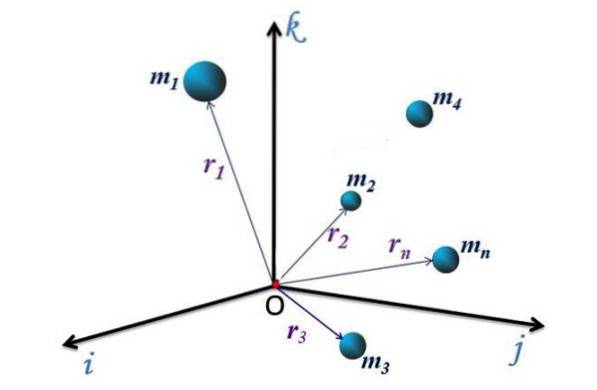
Voor het discrete systeem van Figuur 1, met n deeltjes, elk heeft een positievector gericht van de oorsprong O van het coördinatensysteem naar het punt P (x, y, z) waar het deeltje zich bevindt. Deze vectoren worden aangeduid als r1, rtwee, r3 rn.
De coördinaten van de CM worden berekend met behulp van de volgende vergelijkingen:

Waarbij elk van de massa's van de set wordt weergegeven als m1, mtwee, m3... mn. Merk op dat de som mik is gelijk aan de totale massa M van het samenstel. Als het systeem continu is, worden de sommaties vervangen door integralen.
Elk van de loodrechte richtingen wordt weergegeven door de eenheidsvectoren ik, j Y k, vandaar de positievector van de CM, aangegeven rCM, kan worden uitgedrukt door:
rCM = xCM ik + YCM j + zCM k
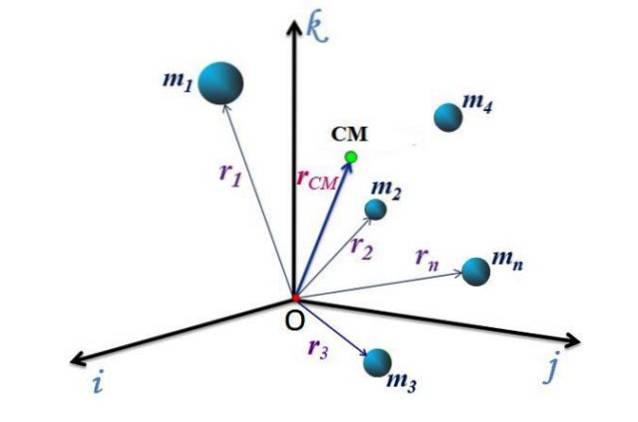
CM-beweging
Zodra de locatie van het zwaartepunt bekend is, zijn de bekende bewegingsvergelijkingen van toepassing. De snelheid van de CM is de eerste afgeleide van de positie ten opzichte van de tijd:

In dit geval heeft het systeem een totaal momentum P. die wordt berekend als het product van de totale massa van het systeem en de snelheid van het massamiddelpunt:
P. = M ∙vCM
Als alternatief kan het totale momentum van het systeem direct worden berekend:
P. = m1v1 + mtweevtwee + m3v3 += ∑ mik vik
Terwijl de versnelling van de CM de afgeleide is van de snelheid:

Forceer op CM
De krachten die op een systeem van deeltjes werken, kunnen zijn:
- Interne krachten door interacties tussen dezelfde deeltjes.
- Externe krachten, veroorzaakt door agenten buiten het systeem.
Aangezien de interne krachten in paren worden weergegeven, van gelijke grootte en richting, maar tegengestelde richtingen, volgens de derde wet van Newton, is het waar dat:
F.int 0
Daarom veranderen de interne krachten de beweging van het geheel niet, maar ze zijn erg belangrijk om de interne energie te bepalen..
Als het systeem geïsoleerd is en er geen externe krachten zijn, is volgens de eerste wet van Newton het zwaartepunt in rust of beweegt het met een uniforme rechtlijnige beweging. Anders ervaart het massamiddelpunt een versnelling die wordt gegeven door:
F.ext = M ∙naarCM
Waar M de totale massa van het systeem is. De bovenstaande vergelijking kan als volgt worden geschreven:

En het betekent dat de externe kracht equivalent is aan de tijdelijke variatie in het momentum, een andere manier om de tweede wet van Newton uit te drukken en dezelfde die de beroemde Engelse natuurkundige in zijn boek gebruikte. Beginsel.
Oefening opgelost
Het massamiddelpunt van een 2-deeltjessysteem bevindt zich op een bepaald moment op de x-as, op de positie x = 2,0 m en beweegt met een snelheid van 5,0 m / s in dezelfde richting en in een positieve richting. Als een van de deeltjes aan de oorsprong is en de andere, met een massa van 0,1 kg, in rust is op x = 8,0 m, bereken dan:
a) De massa van het deeltje dat aan de oorsprong ligt.
b) Hoeveelheid beweging van het systeem
c) Wat is de snelheid van het deeltje bij de oorsprong?
Oplossing voor
Uit de vergelijking voor de positie van het zwaartepunt:
rCM = xCM ik + YCM j + zCM k = 2,0 m ik
Omdat de CM alleen een x-coördinaat heeft, wordt alleen de eerste vergelijking van het eerder gegeven trio gebruikt:

Nu worden de coördinaten vervangen, als het deeltje aan de oorsprong wordt aangeduid als nummer 1 en het andere als nummer 2, zijn de numerieke gegevens:
X1 = 0 m, xtwee = 8,0 m, mtwee = 0,1 kg, xCM = 2,0 m
Resterend:

Oplossing b
De hoeveelheid beweging van het systeem wordt berekend door:
P. = M ∙vCM
De totale massa M is gelijk aan:
M = 0,3 kg + 0,1 kg = 0,4 kg
Daarom:
P. = 0,4 kg ∙ 5,0 m / s ik = 2 kg.m / s ik
Oplossing c
Uit de vergelijking voor P. van een systeem met twee deeltjes, wordt het gewist v1, aangezien de andere gegevens bekend zijn, aangezien de verklaring zegt dat deeltje 2 in rust is, daarom:
vtwee 0
Y P. het ziet er gewoon zo uit:
P. = m1v1
v1 P. / m1 = 2 kg.m / s ik / 0,3 kg 6,67 m / s ik
Referenties
- Duke universiteit. Systemen van deeltjes. Hersteld van: webhome.phy.duke.edu.
- Rex, A. 2011. Fundamentals of Physics. Pearson.
- Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. Ed. Deel 1. Pearson.
- Serway, R., Jewett, J. (2008). Physics for Science and Engineering. Deel 1. 7e. Ed. Cengage Learning.
- Tipler, P. (2006) Fysica voor wetenschap en technologie. 5e editie Deel 1. Editorial Reverté.



Niemand heeft nog op dit artikel gereageerd.