
Distributie F kenmerken en oefeningen opgelost
De F distributie o Fisher-Snedecor-verdeling is de verdeling die wordt gebruikt om de varianties van twee verschillende of onafhankelijke populaties te vergelijken, die elk een normale verdeling volgen.
De verdeling die volgt op de variantie van een reeks steekproeven van een enkele normale populatie is de chikwadraatverdeling (Χtwee) van graad n-1, als elk van de monsters in de set n elementen heeft.
Om de varianties van twee verschillende populaties te vergelijken, is het nodig om een statistisch, dat wil zeggen, een aanvullende willekeurige variabele waarmee we kunnen onderscheiden of beide populaties al dan niet dezelfde variantie hebben.
Genoemde hulpvariabele kan direct het quotiënt zijn van de steekproefvarianties van elke populatie, in welk geval, als dat quotiënt dicht bij de eenheid ligt, er aanwijzingen zijn dat beide populaties vergelijkbare varianties hebben..
Artikel index
- 1 De F-statistiek en zijn theoretische verdeling
- 1.1 Gemiddelde, modus en variantie van de F-verdeling
- 2 Afhandelen van de F-distributie
- 2.1 Tabellen van de F-verdeling
- 2.2 Software voor F-distributie
- 3 Opgeloste oefeningen
- 3.1 Oefening 1
- 3.2 Oefening 2
- 4 referenties
De F-statistiek en de theoretische verdeling ervan
De statistiek van de willekeurige variabele F of F die wordt voorgesteld door Ronald Fisher (1890 - 1962) is de statistiek die het meest wordt gebruikt om de varianties van twee populaties te vergelijken en wordt als volgt gedefinieerd:
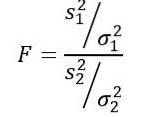
Zijn stwee de steekproefvariantie en σtwee de populatievariantie. Om elk van de twee bevolkingsgroepen te onderscheiden, worden respectievelijk de abonnementen 1 en 2 gebruikt..
Het is bekend dat de chikwadraatverdeling met (n-1) vrijheidsgraden degene is die volgt op de hulpvariabele (of statistische) hieronder gedefinieerd:
Xtwee = (n-1) stwee / σtwee.
Daarom volgt de F-statistiek een theoretische verdeling die wordt gegeven door de volgende formule:
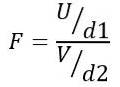
Wezen OF de chikwadraatverdeling met d1 = n1 - 1 vrijheidsgraden voor populatie 1 en V. de chikwadraatverdeling met d2 = n2 - 1 vrijheidsgraden voor bevolking 2.
Het op deze manier gedefinieerde quotiënt is een nieuwe kansverdeling, bekend als F distributie met d1 vrijheidsgraden in de teller en d2 vrijheidsgraden in de noemer.
Gemiddelde, modus en variantie van de F-verdeling
Voor de helft
Het gemiddelde van de F-verdeling wordt als volgt berekend:
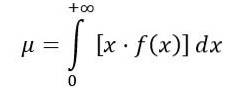
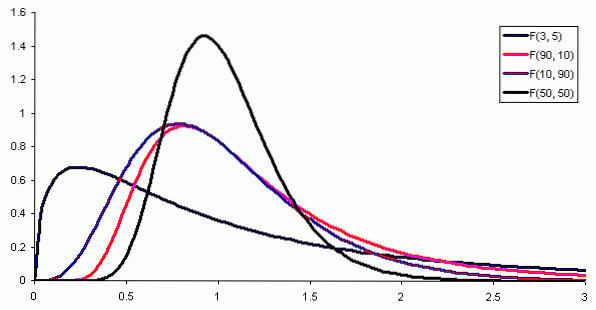
Waar f (x) de kansdichtheid is van de F-verdeling, die wordt weergegeven in figuur 1 voor verschillende combinaties van parameters of vrijheidsgraden.
We kunnen de kansdichtheid f (x) schrijven als functie van de functie Γ (gammafunctie):
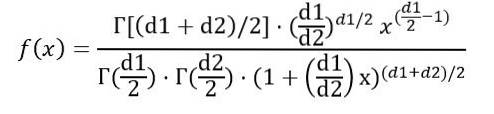
Nadat de hierboven aangegeven integraal is uitgevoerd, wordt geconcludeerd dat het gemiddelde van de F-verdeling met vrijheidsgraden (d1, d2) is:
μ = d2 / (d2 - 2) met d2> 2
Waarbij wordt opgemerkt dat, vreemd genoeg, het gemiddelde niet afhankelijk is van de vrijheidsgraden d1 van de teller.
mode
Aan de andere kant hangt de modus af van d1 en d2 en wordt deze gegeven door:
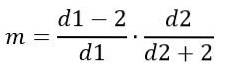
Voor d1> 2.
Variantie van de F-verdeling
De variantie σtwee van de F-verdeling wordt berekend uit de integraal:
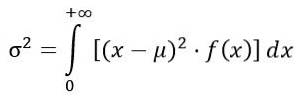
Het verkrijgen van:
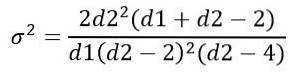
Afhandelen van de F-distributie
Net als andere continue kansverdelingen waarbij gecompliceerde functies betrokken zijn, wordt de afhandeling van de F-verdeling gedaan met behulp van tabellen of software..
Distributietabellen F
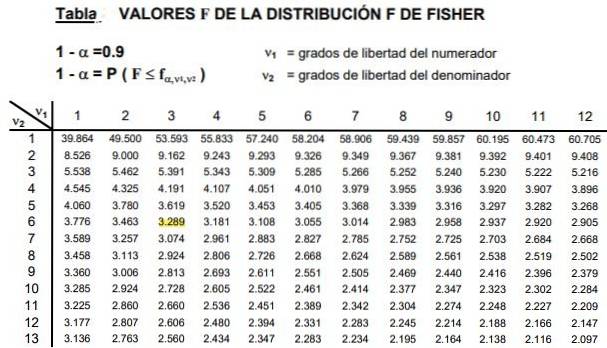
De tabellen bevatten de twee parameters of vrijheidsgraden van de F-verdeling, de kolom geeft de vrijheidsgraad van de teller aan en de rij de vrijheidsgraad van de noemer.
Figuur 2 toont een doorsnede van de tabel van de F-verdeling voor het geval van a mate van belangrijkheid van 10%, dat is α = 0,1. De waarde van F wordt gemarkeerd als d1 = 3 en d2 = 6 met betrouwbaarheidsniveau 1- α = 0.9 dat is 90%.
Software voor F-distributie
Wat betreft de software die de F-distributie afhandelt, is er een grote verscheidenheid aan spreadsheets zoals Excel naar gespecialiseerde pakketten zoals minitab, SPSS Y R om enkele van de bekendste te noemen.
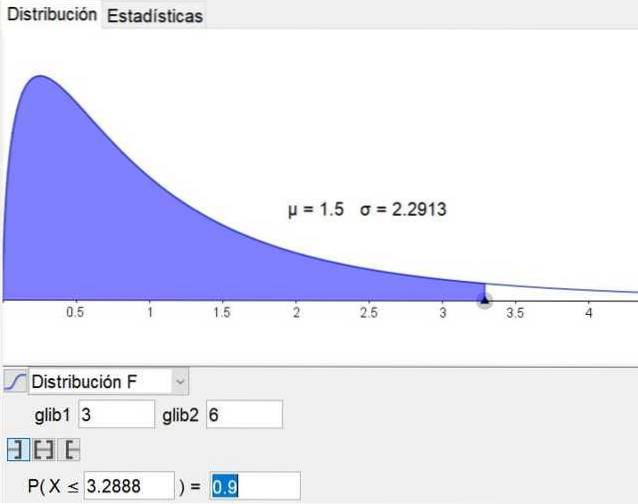
Het is opmerkelijk dat de software voor geometrie en wiskunde geogebra heeft een statistische tool die de belangrijkste distributies bevat, inclusief de F-distributie. Figuur 3 toont de F-distributie voor het geval d1 = 3 en d2 = 6 met betrouwbaarheidsniveau van 90%.
Opgeloste oefeningen
Oefening 1
Beschouw twee steekproeven van populaties met dezelfde populatievariantie. Als steekproef 1 grootte n1 = 5 heeft en steekproef 2 grootte n2 = 10, bepaal dan de theoretische kans dat het quotiënt van hun respectievelijke varianties kleiner is dan of gelijk is aan 2.
Oplossing
Houd er rekening mee dat de F-statistiek wordt gedefinieerd als:
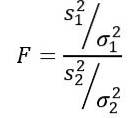
Maar er wordt ons verteld dat de populatieverschillen gelijk zijn, dus voor deze oefening geldt het volgende:
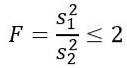
Omdat we de theoretische kans willen weten dat dit quotiënt van steekproefvarianties kleiner is dan of gelijk is aan 2, moeten we het gebied onder de F-verdeling tussen 0 en 2 kennen, dat kan worden verkregen met tabellen of software. Hiervoor moet er rekening mee worden gehouden dat de vereiste F-verdeling d1 = n1 - 1 = 5 - 1 = 4 en d2 = n2 - 1 = 10 - 1 = 9 heeft, dat wil zeggen de F-verdeling met vrijheidsgraden ( 4, 9).
Door gebruik te maken van de statistische tool van geogebra Er werd vastgesteld dat dit gebied 0,82 is, dus er wordt geconcludeerd dat de kans dat het quotiënt van steekproefvarianties kleiner is dan of gelijk is aan 2 82% is.
Oefening twee
Er zijn twee fabricageprocessen voor dunne platen. De variabiliteit van de dikte moet zo laag mogelijk zijn. Van elk proces worden 21 monsters genomen. Het monster uit proces A heeft een standaarddeviatie van 1,96 micron, terwijl het monster uit proces B een standaarddeviatie heeft van 2,13 micron. Welke van de processen heeft de minste variabiliteit? Gebruik een afwijzingsniveau van 5%.
Oplossing
De gegevens zijn als volgt: Sb = 2,13 met nb = 21; Sa = 1,96 met na = 21. Dit betekent dat we moeten werken met een F-verdeling van (20, 20) vrijheidsgraden.
De nulhypothese impliceert dat de populatievariantie van beide processen identiek is, dat wil zeggen, σa ^ 2 / σb ^ 2 = 1. De alternatieve hypothese zou verschillende populatievarianties impliceren.
Vervolgens, onder de aanname van identieke populatievarianties, wordt de berekende F-statistiek gedefinieerd als: Fc = (Sb / Sa) ^ 2.
Omdat het afwijzingsniveau is genomen als α = 0,05, dan is α / 2 = 0,025
De verdeling F (0,025, 20,20) = 0,406, terwijl F (0,975, 20,20) = 2,46.
Daarom is de nulhypothese waar als de berekende F voldoet aan: 0.406≤Fc≤2.46. Anders wordt de nulhypothese verworpen.
Aangezien Fc = (2,13 / 1,96) ^ 2 = 1,18 wordt geconcludeerd dat de Fc-statistiek met een zekerheid van 95% in het acceptatiebereik van de nulhypothese valt. Met andere woorden, met 95% zekerheid hebben beide fabricageprocessen dezelfde populatievariantie..
Referenties
- F Test voor onafhankelijkheid. Hersteld van: saylordotorg.github.io.
- Med Wave. Statistieken toegepast op gezondheidswetenschappen: de F-test Teruggeplaatst van: medwave.cl.
- Waarschijnlijkheden en statistieken. Distributie F. Hersteld van: probayestadistica.com.
- Triola, M. 2012. Elementaire statistieken. 11e. Editie. Addison Wesley.
- UNAM. Distributie F. Hersteld van: asesorias.cuautitlan2.unam.mx.
- Wikipedia. Distributie F. Hersteld van: es.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.