Vergelijking van Henderson-Hasselbalch, voorbeelden, oefening

De Henderson-Hasselbalch-vergelijking is een wiskundige uitdrukking waarmee de pH van een buffer of bufferoplossing kan worden berekend. Het is gebaseerd op de pKa van het zuur en de relatie tussen de concentraties van de geconjugeerde base of zout en het zuur, aanwezig in de bufferoplossing..

De vergelijking werd aanvankelijk ontwikkeld door Lawrence Joseph Henderson (1878-1942) in 1907. Deze chemicus stelde de componenten van zijn vergelijking vast op basis van koolzuur als buffer of buffer..

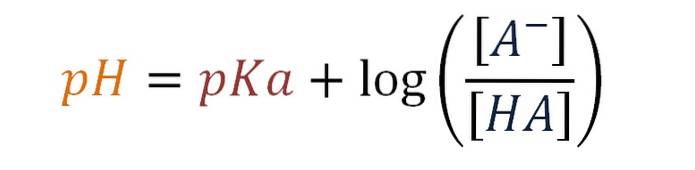
Later introduceerde Karl Albert Hasselbalch (1874-1962) in 1917 het gebruik van logaritmen als aanvulling op de Henderson-vergelijking. De Deense chemicus bestudeerde de reacties van bloed met zuurstof en het effect op de pH-waarde.

Een bufferoplossing kan de pH-veranderingen die een oplossing ondergaat minimaliseren door een volume sterk zuur of base toe te voegen. Het bestaat uit een zwak zuur en zijn sterke geconjugeerde base die snel dissocieert.

Artikel index

• 1 Toelichting
  • 1.1 Wiskundige ontwikkeling
  • 1.2 Vergelijking voor een zwakke basis
• 2 Hoe werkt een buffer?
  • 2.1 Demping
  • 2.2 Buffercapaciteit
• 3 Voorbeelden van Henderson-vergelijkingen
  • 3.1 Acetaat schokdemper
  • 3.2 Koolzuurbuffer
  • 3.3 Lactaatbuffer
  • 3.4 Fosfaatbuffer
  • 3.5 Oxyhemoglobine
  • 3.6 Deoxyhemoglobine
• 4 Opgeloste oefeningen
  • 4.1 Oefening 1
  • 4.2 Oefening 2
  • 4.3 Oefening 3
• 5 referenties

Uitleg

Wiskundige ontwikkeling

Een zwak zuur in een waterige oplossing dissocieert volgens de wet van massaactie, volgens het volgende schema:

HA + H_tweeO ⇌ H⁺    +     NAAR^-

HA is het zwakke zuur en A^- zijn geconjugeerde basis.

Deze reactie is omkeerbaar en heeft een evenwichtsconstante (Ka):

Ka = [H⁺] ·[NAAR^-] / [HA]

Logaritmen nemen:

log Ka = logboek [H⁺] + Logboek [A^-] - log [HA]

Als elke term van de vergelijking wordt vermenigvuldigd met (-1), wordt deze als volgt uitgedrukt:

- log Ka = - log [H⁺] - log [A] + log [HA]

De - log Ka wordt gedefinieerd als pKa en de - log [H⁺] wordt gedefinieerd als pH. Nadat de juiste vervanging is gemaakt, wordt de wiskundige uitdrukking gereduceerd tot:

pKa = pH - log [A^-] + Logboek [HA]

Oplossend voor pH en hergroeperingstermen, wordt de vergelijking als volgt uitgedrukt:

pH = pKa + log [A^-] / [HA]

Dit is de Henderson-Hasselbalch-vergelijking voor een zwakke zuurbuffer.

Vergelijking voor een zwakke basis

Evenzo kan een zwakke basis een buffer vormen, en de Henderson-Hasselbalch-vergelijking daarvoor is als volgt:

pOH = pKb + log [HB] / [B^-​

De meeste bufferoplossingen zijn echter ontstaan, zelfs die van fysiologisch belang, uit de dissociatie van een zwak zuur. Daarom is de meest gebruikte uitdrukking voor de Henderson-Hasselbalch-vergelijking:

pH = pKa + log [A^-] / [HA]

Hoe werkt een buffer?

Dempende werking

De vergelijking van Henderson-Hasselbalch geeft aan dat deze oplossing bestaat uit een zwak zuur en een sterke geconjugeerde base, uitgedrukt als een zout. Deze samenstelling maakt het mogelijk dat de bufferoplossing op een stabiele pH blijft, zelfs wanneer sterke zuren of basen worden toegevoegd..

Wanneer een sterk zuur aan de buffer wordt toegevoegd, reageert het met de geconjugeerde base om een ​​zout en water te vormen. Dit neutraliseert het zuur en zorgt ervoor dat de pH-variatie minimaal is..

Als er nu een sterke base aan de buffer wordt toegevoegd, reageert deze met het zwakke zuur en vormt het water en een zout, waardoor de werking van de toegevoegde base op de pH wordt geneutraliseerd. Daarom is de pH-variatie minimaal.

De pH van een bufferoplossing hangt af van de verhouding tussen de concentraties van de geconjugeerde base en het zwakke zuur, en niet van de absolute waarde van de concentraties van deze componenten. Een bufferoplossing kan worden verdund met water en de pH blijft nagenoeg ongewijzigd.

Buffer capaciteit

De buffercapaciteit hangt ook af van de pKa van het zwakke zuur, evenals de concentraties van het zwakke zuur en de geconjugeerde base. Hoe dichter de pH van de buffer bij de pKa van het zuur ligt, hoe groter de buffercapaciteit..

Evenzo, hoe hoger de concentratie van de componenten van de bufferoplossing, hoe groter de buffercapaciteit..

Voorbeelden van Henderson-vergelijkingen

Acetaat schokdemper

pH = pKa + log [CH₃COO^-] / [CH₃COOH]

pKa = 4,75

Koolzuurbuffer

pH = pKa + log [HCO₃^-] / [H_tweeCO₃​

pKa = 6,11

Het algehele proces dat leidt tot de vorming van het bicarbonaation in een levend organisme is echter als volgt:

CO_twee   +    H._tweeO ⇌ HCO₃^-   +    H.⁺

De CO zijn_twee een gas, de concentratie in oplossing wordt uitgedrukt als een functie van de partiële druk.

pH = pka + log [HCO₃^-] / α pCO_twee

α = 0,03 (mmol / L) / mmHg

pCO_twee is de partiële druk van CO_twee

En dan zou de vergelijking er als volgt uitzien:

pH = pKa + log [HCO₃^-] / 0,03 pCO_twee

Lactaatbuffer

pH = pKa + log [lactaation] / [melkzuur]

pKa = 3,86

Fosfaatbuffer

pH = pKa + log [dibasisch fosfaat] / [monobasisch fosfaat]

pH = pKa + log [HPO₄^twee-] / [H_tweePO₄^-​

pKa = 6,8

Oxyhemoglobine

pH = pKa + log [HbO_twee^-] / [HHbO_twee​

pKa = 6,62

Deoxyhemoglobine

pH = pKa + log [Hb^-] / HbH

pKa = 8,18

Opgeloste oefeningen

Oefening 1

De fosfaatbuffer is belangrijk bij het reguleren van de pH van het lichaam, aangezien zijn pKa (6,8) dicht bij de pH in het lichaam (7,4) ligt. Wat wordt de waarde van de relatie [Na_tweeHPO₄^twee-] / [NaH_tweePO₄^-] van de Henderson-Hasselbalch-vergelijking voor een pH-waarde = 7,35 en een pKa = 6,8?

De NaH-dissociatiereactie_tweePO₄^- het is:

NaH_tweePO₄^-  (zuur) ⇌ NaHPO₄^twee- (basis) + H⁺

pH = pKa + log [Na_tweeHPO₄^twee-] / [NaH_tweePO₄^-​

Oplossend voor de [geconjugeerde base / zuur] -verhouding voor de fosfaatbuffer, hebben we:

7,35 - 6,8 = log [Na_tweeHPO₄^twee-] / [NaH_tweePO₄^-​

0,535 = log [Na_tweeHPO₄^twee-] / [NaH_tweePO₄^-​

10^0,535 = 10^{log [Na2HPO4] / [NaH2PO4]}

3,43 = [Na_tweeHPO₄^twee-] / [NaH_tweePO₄^-​

Oefening 2

Een acetaatbuffer heeft een azijnzuurconcentratie van 0,0135 M en een natriumacetaatconcentratie van 0,0260 M. Bereken de pH van de buffer, wetende dat de pKa voor de acetaatbuffer 4,75 is.

Het dissociatie-evenwicht voor azijnzuur is:

CH₃COOH ⇌ CH₃COO^-   +    H.⁺

pH = pKa + log [CH₃COO^-] / [CH₃COOH]

Vervanging van de waarden die we hebben:

[CH₃COO^-] / [CH₃COOH] = 0,0260 M / 0,0135 M

[CH₃COO^-] / [CH₃COOH] = 1,884

log 1.884 = 0.275

pH = 4,75 + 0,275

pH = 5,025

Oefening 3

Een acetaatbuffer bevat 0,1 M azijnzuur en 0,1 M natriumacetaat. Bereken de pH van de buffer na het toevoegen van 5 ml 0,05 M zoutzuur aan 10 ml van de bovenstaande oplossing.

De eerste stap is om de uiteindelijke concentratie van de HCl te berekenen wanneer deze wordt gemengd met de bufferoplossing:

ViCi = VfCf

Cf = Vi · (Ci / Vf)

= 5 ml · (0,05 M / 15 ml)

= 0,017 M

Zoutzuur reageert met natriumacetaat om azijnzuur te vormen. Daarom neemt de natriumacetaatconcentratie af met 0,017 M en neemt de azijnzuurconcentratie toe met dezelfde hoeveelheid:

pH = pKa + log (0,1 M - 0,017 M) / (0,1 M + 0,017 M)

 pH = pKa + log 0,083 / 0,017

= 4,75 - 0,149

= 4,601

Referenties

1. Whitten, Davis, Peck & Stanley. (2008). Chemie. (8e ed.). CENGAGE Leren.
2. Jimenez Vargas en J. Mª Macarulla. (1984). Fysiologische fysicochemie. 6e editie. Redactioneel Interamericana.
3. Wikipedia. (2020). Henderson-Hasselbalch-vergelijking. Hersteld van: en.wikipedia.org
4. Gurinder Khaira en Alexander Kot. (05 juni 2019). Henderson-Hasselbalch Benadering. Chemie LibreTexts. Hersteld van: chem.libretexts.org
5. Helmenstine, Anne Marie, Ph.D. (29 januari 2020). Vergelijkingsdefinitie van Henderson Hasselbalch. Hersteld van: thoughtco.com
6. De redactie van Encyclopaedia Britannica. (6 februari 2020). Lawrence Joseph Henderson. Encyclopædia Britannica. Hersteld van: britannica.com