De algemene vergelijking van een lijn L is de volgende: Ax + By + C = 0, waarbij A, B en C constanten zijn, x de onafhankelijke variabele en en de afhankelijke variabele.
De helling van een lijn, meestal aangeduid met de letter m, die door de punten P = (x1, y1) en Q = (x0, y0) loopt, is het volgende quotiënt m: = (y1-y0) / (x1 -x0 ).
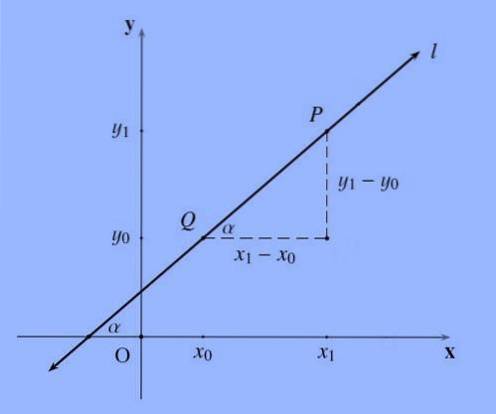
De helling van een lijn vertegenwoordigt op een bepaalde manier de helling; Meer formeel is de helling van een lijn de raaklijn van de hoek die deze vormt met de X-as..
Opgemerkt moet worden dat de volgorde waarin de punten worden genoemd onverschillig is, aangezien (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (x1-x0).
Als er twee punten bekend zijn waar een lijn doorheen gaat, is het gemakkelijk om de helling te berekenen. Maar wat als deze punten niet bekend zijn??
Gegeven de algemene vergelijking van een lijn Ax + By + C = 0, is de helling m = -A / B.
Omdat de helling van de lijn 2/3 is, wordt de gelijkheid -A / B = 2/3 vastgesteld, waarmee we kunnen zien dat A = -2 en B = 3. Dus de algemene vergelijking van een lijn met een helling gelijk aan 2/3 is -2x + 3y + C = 0.
Het moet duidelijk zijn dat als A = 2 en B = -3 worden gekozen, dezelfde vergelijking wordt verkregen. In feite is 2x-3y + C = 0, wat gelijk is aan de vorige vermenigvuldigd met -1. Het teken van C doet er niet toe, aangezien het een algemene constante is.
Een andere observatie die kan worden gemaakt, is dat voor A = -4 en B = 6 dezelfde lijn wordt verkregen, ondanks het feit dat hun algemene vergelijking anders is. In dit geval is de algemene vergelijking -4x + 6y + C = 0.
Het antwoord is ja. Als de helling van een lijn bekend is, zijn er naast de vorige twee manieren om de algemene vergelijking te vinden.
Hiervoor worden de Point-Slope-vergelijking en de Shear-Slope-vergelijking gebruikt..
-De punt-hellingsvergelijking: als m de helling van een lijn is en P = (x0, y0) een punt waar het doorheen gaat, dan wordt de vergelijking y-y0 = m (x-x0) de punt-hellingsvergelijking genoemd.
-De Shear-Slope-vergelijking: als m de helling van een lijn is en (0, b) de snede is van de lijn met de Y-as, dan wordt de vergelijking y = mx + b de Shear-Slope-vergelijking genoemd.
Met behulp van het eerste geval wordt verkregen dat de punt-hellingsvergelijking van een lijn waarvan de helling 2/3 is, wordt gegeven door de uitdrukking y-y0 = (2/3) (x-x0).
Om tot de algemene vergelijking te komen, vermenigvuldig je met 3 aan beide kanten en worden alle termen gegroepeerd aan één kant van de gelijkheid, waarmee wordt verkregen dat -2x + 3y + (2 × 0-3y0) = 0 de algemene vergelijking is van de regel, waarbij C = 2 × 0-3y0.
Als het tweede geval wordt gebruikt, wordt verkregen dat de vergelijking Cut-Slope van een lijn waarvan de helling 2/3 is, y = (2/3) x + b is.
Nogmaals, door aan beide zijden met 3 te vermenigvuldigen en alle variabelen te groeperen, krijgen we -2x + 3y-3b = 0. Dit laatste is de algemene vergelijking van de lijn waarbij C = -3b.
Als we beide gevallen goed bekijken, kunnen we zien dat het tweede geval gewoon een specifiek geval is van het eerste (wanneer x0 = 0).
Niemand heeft nog op dit artikel gereageerd.