
Eneagon-eigenschappen, hoe een eneagon te maken, voorbeelden

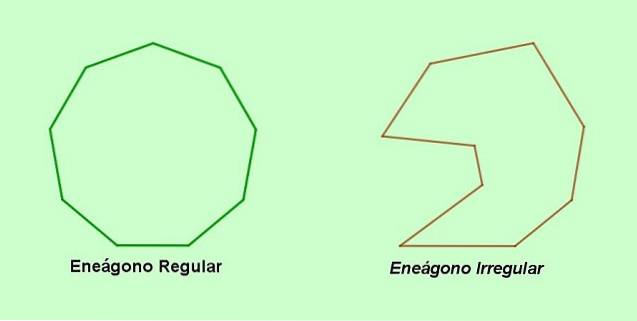
EEN eneagon is een veelhoek met negen zijden en negen hoekpunten, die al dan niet regelmatig zijn. De naam eneágono komt uit het Grieks en bestaat uit de Griekse woorden ennea (negen en Gonon (hoek).
Een alternatieve naam voor de negenzijdige veelhoek is nonagon, een woord dat uit het Latijn komt nonus (negen en Gonon (hoekpunt). Aan de andere kant, als de zijkanten of hoeken van de enegon ongelijk aan elkaar zijn, dan hebben we een onregelmatige enegon. Als, aan de andere kant, de negen zijden en de negen hoeken van de enegon gelijk zijn, dan is het a regelmatige enegon.
Artikel index
- 1 Eigenschappen van de enegon
- 1.1 Regelmatige enegon
- 1.2 Gebied van een enegon bekend de zijkant en de apothema
- 1.3 Gebied van een bekende enegon de zijkant
- 1.4 Omtrek van de reguliere enegon kent zijn kant
- 1.5 Omtrek van de enegon bekende zijn straal
- 2 Hoe maak je een regelmatige eneagon
- 3 voorbeelden
- 3.1 Voorbeeld 1
- 3.2 Voorbeeld 2
- 4 referenties
Eneagon-eigenschappen
Voor een veelhoek met n zijden is de som van de binnenhoeken:
(n - 2) * 180º
In de enegon zou het n = 9 zijn, dus de som van de interne hoeken is:
Sa = (9 - 2) * 180º = 7 * 180º = 1260º
In elke veelhoek is het aantal diagonalen:
D = n (n - 3) / 2 en in het geval van de enegon, aangezien n = 9, hebben we dan die D = 27.
Regelmatige enegon
In de reguliere eneagon of nonagon zijn er negen (9) interne hoeken van gelijke grootte, daarom meet elke hoek een negende van de totale som van de interne hoeken..
De maat van de interne hoeken van een enegon is dan 1260º / 9 = 140º.
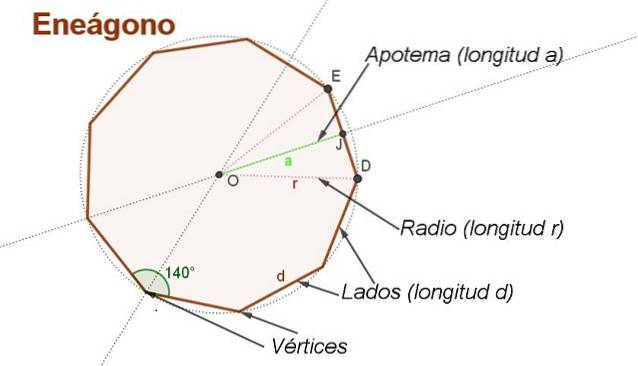
De formule afleiden voor de oppervlakte van een regelmatige enegon met zijde d het is handig om enkele hulpconstructies te maken, zoals die in figuur 2.
Het centrum is gelegen OF het traceren van de middelloodlijnen van twee aangrenzende zijden. Het centrum OF op gelijke afstand van hoekpunten.
Een straal van lengte r is het segment dat vanuit het midden gaat OF naar een hoekpunt van de enegon. De stralen zijn weergegeven in figuur 2. OD Y OE van lengte r.
De apothema is het segment dat van het midden naar het midden van een kant van de enegon gaat. Bijvoorbeeld PB is een apothema waarvan de lengte is naar.
Gebied van een bekende enegon de zijkant en de apothema
We beschouwen de driehoek ODE van figuur 2. De oppervlakte van deze driehoek is het product van de basis VAN voor de hoogte PB gedeeld door 2:
Oppervlakte ODE (DE * PB) / 2 (d * a) / 2
Omdat er 9 driehoeken van gelijke oppervlakte in de enegon zijn, wordt geconcludeerd dat de oppervlakte ervan is:
Eneagon gebied (9/2) (d * a)
Gebied van een bekende enegon de zijkant
Als alleen de lengte d van de zijkanten van de enegon bekend is, dan is het nodig om de lengte van het apothema te vinden om de formule uit de vorige paragraaf te kunnen toepassen.
We beschouwen de driehoek OOG rechthoek in J (zie figuur 2). Als de tangens trigonometrische verhouding wordt toegepast, verkrijgen we:
zo(OEJ PB Ex.
De engel ∡OEJ = 140º / 2 = 70º, te zijn EO bissectrice van de interne hoek van de enegon.
Aan de andere kant, PB is de apothema van lengte naar.
Dan als J is het middelpunt van ED het volgt dat EJ = d / 2.
Als we de vorige waarden in de tangensrelatie vervangen, hebben we:
bruin (70º) = een / (d / 2).
Nu wissen we de lengte van de apothema:
a = (d / 2) geelbruin (70º).
Het vorige resultaat wordt vervangen in de gebiedsformule om het volgende te krijgen:
Eneagon gebied (9/2) (d * a) = (9/2) d * (d / 2) geelbruin (70º))
Ten slotte vinden we de formule waarmee het gebied van de reguliere enegon kan worden bepaald als alleen de lengte bekend is d van zijn zijkanten:
Eneagon gebied = (9/4) dtwee geelbruin (70º) = 6.1818 dtwee
Omtrek van regelmatige enegon kende zijn kant
De omtrek van een veelhoek is de som van de zijden. In het geval van de enegon, omdat elk van de zijkanten een lengte meet d, zijn omtrek is de som van negen keer d, namelijk:
Omtrek = 9 d
Omtrek van de enegon bekende zijn straal
Gezien de driehoek OOG rechthoek in J (zie figuur 2), wordt de trigonometrische cosinusverhouding toegepast:
cos (OEJ Ex OE = (d / 2) / r
Waar komt het vandaan:
d = 2r cos (70º)
Als we dit resultaat vervangen, krijgen we de formule voor de omtrek als functie van de straal van de enegon:
Omtrek = 9 d 18 r cos (70º) = 6.1564 r
Hoe maak je een regelmatige eneagon
1- Om een regelmatig eneagon te bouwen, met een liniaal en een kompas, begin je bij de omtrek c dat omschrijft de enegon. (zie figuur 3)
2- Twee loodrechte lijnen worden door het midden O van de omtrek getrokken. Vervolgens worden de snijpunten A en B van een van de lijnen gemarkeerd met de omtrek.
3- Met het kompas, gecentreerd op het snijpunt B en opening gelijk aan de straal BO, wordt een boog getekend die de oorspronkelijke omtrek onderschept op een punt C.
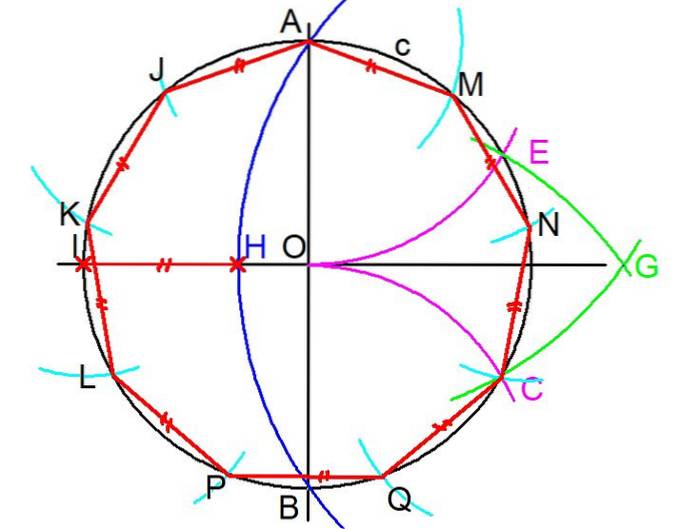
4- De vorige stap wordt herhaald, maar door een middelpunt te maken op A en straal AO, wordt een boog getekend die de omtrek c op punt E onderschept.
5- Met opening AC en midden in A wordt een omtrekboog getekend. Evenzo wordt bij opening BE en middelpunt B een andere boog getekend. Het snijpunt van deze twee bogen is gemarkeerd als punt G.
6- Centrerend bij G en opening GA, wordt een boog getekend die de secundaire as (in dit geval horizontaal) op punt H onderschept. Het snijpunt van de secundaire as met de oorspronkelijke omtrek c is gemarkeerd als I.
7- De lengte van het segment IH is gelijk aan de lengte d van de zijkant van de enegon.
8- Met kompasopening IH = d, worden achtereenvolgens de bogen van straal A AJ middelpunt A, straal AK middelpunt J, straal KL middelpunt K en straal LP middel L achtereenvolgens getekend.
9- Evenzo worden vanaf A en vanaf de rechterkant bogen met straal IH = d getekend die de punten M, N, C en Q op de oorspronkelijke omtrek c markeren.
10- Ten slotte worden de segmenten AJ, JK, KL, LP, AM, MN, NC, CQ en tenslotte PB getekend.
Opgemerkt moet worden dat de constructiemethode niet helemaal exact is, aangezien kan worden vastgesteld dat de laatste zijde PB 0,7% langer is dan de andere zijden. Tot op heden is er geen bekende constructiemethode met een liniaal en kompas die 100% nauwkeurig is..
Voorbeelden
Hier zijn enkele uitgewerkte voorbeelden.
voorbeeld 1
U wilt een gewone enegon bouwen waarvan de zijkanten 2 cm lang zijn. Welke straal moet de omtrek hebben die deze omschrijft, zodat bij het toepassen van de hiervoor beschreven constructie het gewenste resultaat wordt verkregen?
Oplossing:
In een vorige paragraaf werd de formule afgeleid die de straal r van de omgeschreven cirkel relateert aan de zijde d van een regelmatige enegon:
d = 2r cos (70º)
Oplossend voor r uit de vorige uitdrukking hebben we:
r = d / (2 cos (70º)) = 1,4619 * d
Door de waarde d = 2 cm in de vorige formule te vervangen, wordt een straal r van 2,92 cm verkregen.
Voorbeeld 2
Wat is de oppervlakte van een gewone enegon met een zijde van 2 cm?
Oplossing:
Om deze vraag te beantwoorden, moeten we verwijzen naar de eerder getoonde formule waarmee we het gebied van een bekende enegon kunnen vinden door de lengte d van zijn zijde:
Eneagon gebied = (9/4) dtwee geelbruin (70º) = 6.1818 dtwee
Als we d vervangen door de waarde van 2 cm in de vorige formule, krijgen we:
Eneagon gebied = 24,72 cm
Referenties
- C. E. A. (2003). Geometrie-elementen: met oefeningen en geometrie van het kompas. Universiteit van Medellin.
- Campos, F., Cerecedo, F. J. (2014). Wiskunde 2. Grupo Redactie Patria.
- Freed, K. (2007). Ontdek Polygonen. Benchmark Onderwijsbedrijf.
- Hendrik, V. (2013). Gegeneraliseerde polygonen. Birkhäuser.
- IGER. (s.f.). Wiskunde eerste semester Tacaná. IGER.
- Jr. geometrie. (2014). Veelhoeken. Lulu Press, Inc.
- Miller, Heeren en Hornsby. (2006). Wiskunde: redeneren en toepassingen (tiende editie). Pearson Education.
- Patiño, M. (2006). Wiskunde 5. Redactioneel Progreso.



Niemand heeft nog op dit artikel gereageerd.