
Beschrijvende statistiekgeschiedenis, kenmerken, voorbeelden, concepten
De Beschrijvende statistieken is de tak van de statistiek die verantwoordelijk is voor het verzamelen en organiseren van informatie over het gedrag van systemen met veel elementen, algemeen bekend onder de naam van bevolking.
Om dit te doen, gebruikt het numerieke en grafische technieken, waarmee het informatie presenteert, zonder voorspellingen of conclusies te trekken over de populatie waaruit het afkomstig is..

Artikel index
- 1 Geschiedenis
- 1.1 Ancient Age
- 1.2 Renaissance
- 1.3 Moderne tijd
- 2 Kenmerken van beschrijvende statistieken
- 3 Waar zijn beschrijvende statistieken voor??
- 3.1 Economie
- 3.2 Fysica en mechanica
- 3.3 Geneeskunde
- 3.4 Voeding
- 4 Voorbeelden van beschrijvende statistieken
- 4.1 Voorbeeld 1
- 4.2 Voorbeeld 2
- 4.3 Voorbeeld 3
- 5 Basisconcepten van beschrijvende statistieken
- 5.1 Bevolking
- 5.2 Voorbeeld
- 5.3 Variabele
- 5.4 Maatregelen van centrale tendens
- 5.5 Dispersiemetingen
- 6 Interessante onderwerpen
- 7 referenties
Verhaal
Oude leeftijd
Statistiek vindt zijn oorsprong in de menselijke behoefte om de informatie te organiseren die nodig is voor zijn overleving en welzijn, en om te anticiperen op de gebeurtenissen die erop van invloed zijn. De grote beschavingen uit de oudheid hebben verslagen achtergelaten over kolonisten, geïnde belastingen, hoeveelheid oogsten en de omvang van legers.
Tijdens zijn lange regering gaf Ramses II (1279-1213 v.Chr.) Bijvoorbeeld opdracht tot een telling van landen en inwoners in Egypte, dat toen ongeveer 2 miljoen inwoners telde..
Evenzo vertelt de bijbel dat Mozes een volkstelling hield om erachter te komen hoeveel soldaten de twaalf stammen van Israël hadden.
Ook in het oude Griekenland werden mensen en middelen geteld. De Romeinen, bekend om hun hoge organisatie, registreerden periodiek de bevolking en stelden om de vijf jaar tellingen op, inclusief territoria en bronnen..
Renaissance
Na het verval van Rome waren belangrijke statistische gegevens schaars, tot de komst van de Renaissance, toen de statistiek weer opkwam als hulpmiddel bij de besluitvorming.
Aan het einde van de zeventiende eeuw werd de waarschijnlijkheidstheorie geboren, het resultaat van de neiging van mensen voor kansspelen, die Statistics de wiskundige nauwkeurigheid gaf die er een op zichzelf staande wetenschap van maakte..
Moderne tijd
Een nieuwe impuls kwam met de theorie van fouten en kleinste kwadraten in de 19e eeuw, die werd gevolgd door de methode van correlatie tussen variabelen, om de relatie daartussen kwantitatief te beoordelen..
Tot uiteindelijk, in de 20e eeuw, verspreidde de statistiek zich naar elke tak van wetenschap en techniek als een onmisbaar hulpmiddel bij het oplossen van problemen..
Beschrijvende statistische kenmerken
Beschrijvende statistieken worden gekenmerkt door:
- Organiseer de verzamelde informatie in de vorm van gegevens en grafieken. De grafieken kunnen divers zijn: onder andere histogrammen, frequentiepolygonen, taartvormige diagrammen..
- Verdeel de gegevens in frequentiebereiken om het beheer ervan te vergemakkelijken. Gebruik rekenkunde om de meest representatieve waarden van de gegevens te vinden, door middel van metingen van centrale tendens, en analyseer hun spreiding.
- Bepaal de vorm van de verdelingen, hun symmetrie, of ze gecentreerd of scheef zijn, en of ze puntig of eerder afgeplat zijn.
Waar zijn beschrijvende statistieken voor?
Telkens wanneer gegevens moeten worden verzameld, georganiseerd en gepresenteerd, zijn beschrijvende statistieken essentieel in wetenschapsgebieden die met veel elementen en hoeveelheden te maken hebben, evenals in veel menselijke activiteiten: economie, politiek, gezondheid, sport en meer..
Hier zijn enkele voorbeelden:
Economie
Beschrijvende statistieken hebben betrekking op het consequent vastleggen en ordenen van gegevens over bevolkingsgroepen en hun leeftijden, inkomen, investeringen, inkomsten en uitgaven. Op deze manier plannen overheden en instellingen verbeteringen en investeren ze de middelen op de juiste manier..
Met zijn hulp worden aankopen, verkopen, retouren en efficiëntie van diensten bewaakt. Om deze reden zijn statistieken essentieel bij de besluitvorming.
Fysica en mechanica
Fysica en mechanica gebruiken statistiek om continue media te bestuderen, die uit een groot aantal deeltjes bestaan, zoals atomen en moleculen. Het blijkt dat het niet mogelijk is om ze allemaal afzonderlijk te volgen..
Maar door het globale gedrag van het systeem (bijvoorbeeld een deel van het gas) vanuit macroscopisch oogpunt te bestuderen, is het mogelijk om gemiddelden te vinden en macroscopische variabelen te definiëren om hun eigenschappen te kennen. Een voorbeeld hiervan is de kinetische theorie van gassen.
Geneesmiddel
Het is een essentieel instrument bij het monitoren van ziekten, vanaf hun oorsprong en tijdens hun evolutie, evenals de doeltreffendheid van behandelingen.
Statistieken die morbiditeitscijfers, genezingspercentages, incubatie- of ontwikkelingstijden van een ziekte, de leeftijd waarop deze gewoonlijk voorkomt en vergelijkbare gegevens beschrijven, zijn nodig bij het ontwerpen van de meest effectieve behandelingen..
Voeding
Een van de vele toepassingen van beschrijvende statistieken is het vastleggen en ordenen van gegevens over voedselconsumptie in verschillende populaties: de hoeveelheid, kwaliteit en de meest geconsumeerde, naast vele andere observaties die experts interesseren..
Beschrijvende statistische voorbeelden
Hier zijn enkele voorbeelden die illustreren hoe nuttig beschrijvende statistiekhulpmiddelen zijn om beslissingen te nemen:
voorbeeld 1

De onderwijsautoriteiten van een land plannen institutionele verbeteringen. Stel dat u een nieuw schoolkantinesysteem gaat implementeren.
Hiervoor is het nodig om gegevens te hebben over de studentenpopulatie, bijvoorbeeld het aantal studenten per klas, hun leeftijd, geslacht, lengte, gewicht en sociaaleconomische status. Deze informatie wordt vervolgens gepresenteerd in de vorm van tabellen en grafieken..
Voorbeeld 2
Om het lokale voetbalteam bij te houden en nieuwe aanwinsten te doen, houden managers het aantal gespeelde, gewonnen, gelijkgespeelde en verloren wedstrijden bij, evenals het aantal doelpunten, de doelpuntenmakers en hoe ze wisten te scoren: vrije trap, helft rechtbank, straffen, met linker- of rechterbeen, onder andere details.
Voorbeeld 3
Een ijssalon heeft verschillende smaken ijs en wil zijn verkoop verbeteren, daarom voeren de eigenaren een onderzoek uit waarbij ze het aantal klanten tellen, ze verdelen in groepen naar geslacht en leeftijdscategorie.
In dit onderzoek worden bijvoorbeeld de favoriete ijssmaak en de best verkochte presentatie vastgelegd. En met de verzamelde gegevens plannen ze de aankopen van de smaken en de containers en accessoires die nodig zijn voor hun bereiding..
Beschrijvende basisprincipes van statistieken
Deze fundamentele concepten zijn nodig om statistische technieken toe te passen, laten we eens kijken:
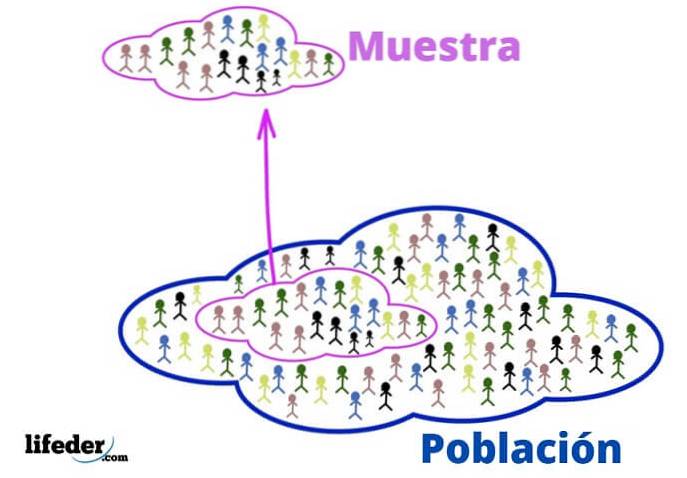
Bevolking
In de statistische context verwijst de populatie naar het universum of de groep waaruit de informatie afkomstig is.
Ze gaan niet altijd over mensen, aangezien het groepen dieren, planten of objecten kunnen zijn, zoals auto's, atomen, moleculen en zelfs gebeurtenissen en ideeën..
Tonen
Als de populatie erg groot is, wordt daaruit een representatieve steekproef getrokken en geanalyseerd, zonder relevante informatie te verliezen..
Het kan willekeurig worden gekozen, of volgens een aantal criteria die eerder door de analist zijn vastgesteld. Het voordeel is dat het als een subset van de bevolking veel beter beheersbaar is.
Variabel
Het verwijst naar de reeks waarden die een bepaald kenmerk van de bevolking kan aannemen. Een onderzoek kan verschillende variabelen bevatten, zoals leeftijd, geslacht, gewicht, academisch niveau, burgerlijke staat, inkomen, temperatuur, kleur, tijd en nog veel meer.
De variabelen kunnen van verschillende aard zijn, dus er zijn criteria om ze te classificeren en om ze de meest geschikte behandeling te geven.
Categorische variabelen en numerieke variabelen
Afhankelijk van de manier waarop ze worden gemeten, kunnen de variabelen zijn:
-Categorisch
-Numeriek
Categorische variabelen, ook wel kwalitatief, vertegenwoordigen kwaliteiten zoals de burgerlijke staat van een persoon, die ongehuwd, getrouwd, gescheiden of weduwe kan zijn.
In plaats daarvan numerieke variabelen of kwantitatief, kunnen worden gemeten, zoals leeftijd, tijd, gewicht, inkomen en meer.
Discrete variabelen en continue variabelen
Discrete variabelen nemen alleen discrete waarden aan, zoals hun naam al aangeeft. Voorbeelden hiervan zijn het aantal kinderen in een gezin, hoeveel vakken er in een bepaald vak zitten en het aantal auto's op een parkeerplaats.
Deze variabelen nemen niet altijd gehele getallen aan, aangezien er ook fractionele zijn.
Aan de andere kant laten continue variabelen oneindig veel waarden toe binnen een bepaald bereik, zoals het gewicht van een persoon, de pH van het bloed, de tijd van een telefonisch consult en de diameter van voetballen..
Maatregelen van centrale tendens
Ze geven een idee van de algemene trend die door de gegevens wordt gevolgd. We noemen de drie meest gebruikte centrale maatregelen:
-Voor de helft
-Mediaan
-mode
Voor de helft
Gelijk aan het gemiddelde van de waarden. Het wordt berekend door alle waarnemingen bij elkaar op te tellen en te delen door het totale aantal:

mode
Het is de waarde die het meest wordt herhaald in een dataset, de meest of de meest voorkomende, aangezien er in een distributie meer dan één modus kan zijn.
Mediaan
Bij het sorteren van een set gegevens is de mediaan de centrale waarde van alle gegevens.
Maatregelen van verspreiding
Ze wijzen op de variabiliteit van de gegevens en geven een idee van hoe ver of verspreid ze zijn verwijderd van de centrale metingen. De meest gebruikte zijn:
Rang
Het is het verschil tussen de grootste waarde xM. en de kleinste xm uit een dataset:
Rang = xM. - Xm
Variantie
Meet hoe ver de gegevens verwijderd zijn van de gemiddelde waarde. Hiervoor wordt een gemiddelde gemaakt, maar met de verschillen tussen elke waarde xik en het gemiddelde, vierkant om te voorkomen dat ze elkaar opheffen. Het wordt meestal aangeduid met de Griekse letter σ in het kwadraat, of met stwee

De variantie heeft niet dezelfde eenheden als de gegevens, dus de standaarddeviatie wordt gedefinieerd als de vierkantswortel van de variantie en wordt aangeduid als σ of s:

In plaats van elke gegevens afzonderlijk in aanmerking te nemen, verdient het de voorkeur om ze in bereiken te groeperen, wat het werk vergemakkelijkt, vooral als er veel waarden zijn. Als u bijvoorbeeld met kinderen op een school werkt, kunnen ze worden ingedeeld in leeftijdscategorieën: 0 tot 6 jaar, 6 tot 12 jaar en 12 tot 18 jaar.
Grafieken
Ze zijn een geweldige manier om de distributie van de gegevens in één oogopslag te zien en bevatten alle informatie die is verzameld in de tabellen en tabellen, maar veel goedkoper.
Er is een grote variatie: met staven, lineair, cirkelvormig, stengel en blad, histogrammen, frequentiepolygonen en pictogrammen. Voorbeelden van statistische grafieken worden getoond in figuur 3..
Thema's van belang
Takken van statistieken.
Statistische variabelen.
Bevolking en steekproef.
Inferentiële statistieken.
Referenties
- Faraldo, P. Statistieken en onderzoeksmethodologie. Hersteld van: eio.usc.es.
- Fernández, S. 2002. Beschrijvende statistieken. 2e. Editie. ESIC-redactie. Hersteld van: Google Books.
- Geschiedenis van de statistiek. Hersteld van: eumed.net.
- Ibañez, P. 2010. Wiskunde II. Competentiebenadering. Cengage leren.
- Monroy, S. 2008. Beschrijvende statistieken. 1e. Editie. Nationaal Polytechnisch Instituut van Mexico.
- Universum-formules. Beschrijvende statistieken. Hersteld van: universoformulas.com.



Niemand heeft nog op dit artikel gereageerd.