
Millikan-experimentprocedure, uitleg, belang
De millikan experiment, uitgevoerd door Robert Millikan (1868-1953) samen met zijn student Harvey Fletcher (1884-1981), begon in 1906 en had tot doel de eigenschappen van elektrische lading te bestuderen, door de beweging van duizenden druppels olie in het midden van een uniform te analyseren elektrisch veld.
De conclusie was dat de elektrische lading geen willekeurige waarde had, maar in veelvouden van 1,6 x 10 kwam-19 C, de fundamentele lading van het elektron. Bovendien werd de massa van het elektron gevonden.
Eerder was de natuurkundige J.J. Thompson had experimenteel de lading-massa-relatie gevonden van dit elementaire deeltje, dat hij "bloedlichaampje" noemde, maar niet de waarden van elke grootte afzonderlijk..
Uit dit verband tussen lading en massa en de lading van het elektron werd de waarde van zijn massa bepaald: 9,11 x 10-31 Kg.
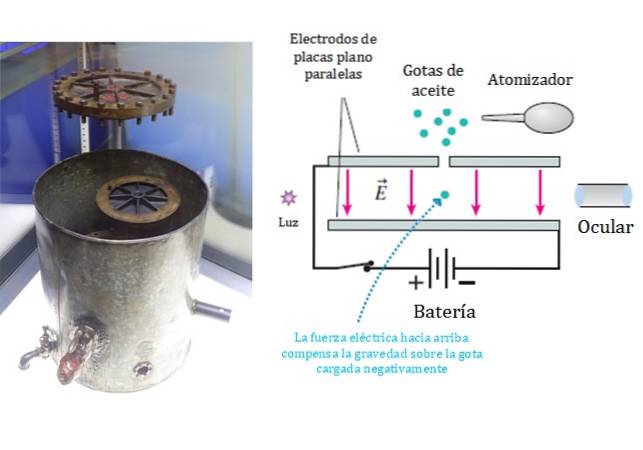
Om hun doel te bereiken, gebruikten Millikan en Fletcher een verstuiver waarmee een fijne nevel van oliedruppeltjes werd gesproeid. Een deel van de druppeltjes werd elektrisch geladen door wrijving in het mondstuk.
De geladen druppels bezinken langzaam op evenwijdige vlakke plaatelektroden, waar een paar door een klein gaatje in de bovenplaat gingen, zoals weergegeven in het diagram in figuur 1.
Binnen de parallelle platen is het mogelijk om een uniform elektrisch veld loodrecht op de platen te creëren, waarvan de grootte en polariteit werden gecontroleerd door de spanning te wijzigen..
Het gedrag van de druppels werd waargenomen door de binnenkant van de platen te verlichten met een helder licht..
Artikel index
- 1 Toelichting op het experiment
- 1.1 De massa van de oliedruppel
- 2 Belang
- 2.1 Drops met verschillende ladingen
- 3 Voorbeeld
- 3.1 Een druppel olie laten zweven
- 4 referenties
Toelichting op het experiment
Als de druppel een lading heeft, oefent het veld tussen de platen een kracht uit die de zwaartekracht tegengaat..
En als het ook lukt om te blijven hangen, betekent dit dat het veld een opwaartse verticale kracht uitoefent, die de zwaartekracht precies in evenwicht houdt. Deze voorwaarde is afhankelijk van de waarde van wat, de last van de drop.
Millikan merkte inderdaad op dat na het omdraaien van het veld, sommige druppels werden opgeschort, andere begonnen te stijgen of bleven dalen.
Door de waarde van het elektrische veld aan te passen - bijvoorbeeld door middel van een variabele weerstand - zou een druppel binnen de platen kunnen blijven hangen. Hoewel het in de praktijk niet gemakkelijk te bereiken is, zal als het gebeurt, alleen de kracht die wordt uitgeoefend door het veld en de zwaartekracht op de druppel inwerken..
Als de massa van de druppel is m en zijn lading is wat, wetende dat de kracht evenredig is met het aangelegde veld van grootte EN, De tweede wet van Newton stelt dat beide krachten in evenwicht moeten zijn:
mg = q.E
q = mg / E
De waarde van g, de versnelling van de zwaartekracht is bekend, evenals de grootte EN van het veld, dat afhangt van de spanning V. gevestigd tussen de platen en de opening ertussen L., Wat:
E = V / L
De vraag was om de massa van de kleine druppel olie te vinden. Zodra dit is bereikt, bepaalt u de belasting wat het is perfect mogelijk. Dat natuurlijk m Y wat zijn respectievelijk de massa en lading van de oliedruppel, niet het elektron.
Maar ... de druppel wordt geladen omdat hij elektronen verliest of wint, dus de waarde is gerelateerd aan de lading van dat deeltje.
De massa van de oliedruppel
Het probleem van Millikan en Fletcher was om de massa van een druppel te bepalen, geen gemakkelijke taak vanwege het kleine formaat..
Als je de dichtheid van de olie kent, kan de massa worden opgelost als je het volume van de druppel hebt. Maar het volume was ook erg klein, dus conventionele methoden waren niet nuttig..
De onderzoekers wisten echter dat zulke kleine objecten niet vrij vallen, aangezien de weerstand van de lucht of van de omgeving ingrijpt door hun beweging te vertragen. Hoewel het deeltje, wanneer het wordt losgelaten met het veld eraf, een versnelde verticale beweging en naar beneden ervaart, valt het uiteindelijk met constante snelheid..
Deze snelheid wordt "eindsnelheid" of "grenssnelheid" genoemd, die in het geval van een bol afhangt van de straal en de viscositeit van de lucht..
Bij gebrek aan een veld, maten Millikan en Fletcher de tijd die de druppels nodig hadden om te vallen. Ervan uitgaande dat de druppels bolvormig waren en met de waarde van de viscositeit van de lucht, slaagden ze erin om de straal indirect te bepalen uit de eindsnelheid.
Deze snelheid wordt gevonden door de wet van Stokes toe te passen en hier is de vergelijking:

-vt is de eindsnelheid
-R is de straal van de druppel (bolvormig)
-η is de viscositeit van lucht
-ρ is de dichtheid van de druppel
Belang
Het experiment van Millikan was cruciaal, omdat het verschillende belangrijke aspecten in de natuurkunde aan het licht bracht:
I) De elementaire lading is die van het elektron, waarvan de waarde 1,6 x 10 is -19 C, een van de fundamentele constanten van de wetenschap.
II) Elke andere elektrische lading komt in veelvouden van de fundamentele lading.
III) De lading van het elektron en de lading-massa-relatie van J.J. Thomson, was het mogelijk om de massa van het elektron te bepalen.
III) Op het niveau van deeltjes zo klein als elementaire deeltjes zijn de gravitatie-effecten verwaarloosbaar in vergelijking met elektrostatica.

Millikan ontving voor deze ontdekkingen in 1923 de Nobelprijs voor natuurkunde. Zijn experiment is ook relevant omdat hij deze fundamentele eigenschappen van elektrische lading heeft bepaald, uitgaande van een eenvoudig instrumentarium en wetten toepast die bij iedereen bekend zijn..
Millikan kreeg echter kritiek omdat hij zonder aanwijsbare reden veel observaties in zijn experiment had verworpen om de statistische fout van de resultaten te verminderen en ze 'presentabeler' te maken..
Druppels met verschillende ladingen
Millikan mat vele, vele druppels in zijn experiment en niet allemaal waren het olie. Hij probeerde ook kwik en glycerine. Zoals gezegd begon het experiment in 1906 en duurde het een paar jaar. Drie jaar later, in 1909, werden de eerste resultaten gepubliceerd.
Gedurende deze tijd verkreeg hij een verscheidenheid aan geladen druppels door röntgenstralen door de platen te laten vallen om de lucht ertussen te ioniseren. Op deze manier komen geladen deeltjes vrij die de druppels kunnen opnemen.
Bovendien concentreerde hij zich niet alleen op de zwevende druppels. Millikan merkte op dat wanneer de druppels opstegen, de stijgsnelheid ook varieerde naargelang de geleverde belasting..
En als de druppel daalde, veranderde deze extra lading die werd toegevoegd dankzij de tussenkomst van de röntgenstralen, de snelheid niet, omdat elke massa elektronen die aan de druppel wordt toegevoegd minuscuul is in vergelijking met de massa van de druppel zelf..
Ongeacht de hoeveelheid lading die hij toevoegde, ontdekte Millikan dat alle verworven drops gehele veelvouden van een bepaalde waarde opladden, namelijk en, de fundamentele eenheid, die, zoals we al zeiden, de lading van het elektron is.
Millikan scoorde aanvankelijk 1.592 x 10-19 C voor deze waarde, iets minder dan momenteel wordt geaccepteerd, namelijk 1.602 x 10-19 C. De verhouding kan de waarde zijn die u in de vergelijking aan de viscositeit van de lucht hebt gegeven om de eindsnelheid van de druppel te bepalen..
Voorbeeld
Een druppel olie laten zweven
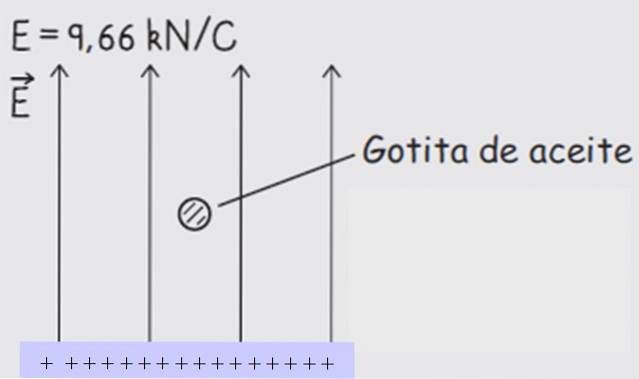
We zien het volgende voorbeeld. Een oliedruppel heeft een dichtheid ρ = 927 kg / m3 en wordt vrijgegeven in het midden van de elektroden met het elektrische veld uit. De druppel bereikt snel de eindsnelheid, waarmee de straal wordt bepaald, waarvan de waarde R = 4,37 x10 blijkt te zijn-7 m.
Het uniforme veld is ingeschakeld, verticaal naar boven gericht en heeft een magnitude van 9,66 kN / C. Op deze manier wordt de druppel in rust opgeschort..
Het vraagt:
a) Bereken de druppellading
b) Zoek uit hoe vaak de elementaire lading in de lading van de druppel zit.
c) Bepaal indien mogelijk het teken van de lading.
Oplossing voor
Eerder werd de volgende uitdrukking afgeleid voor een druppel in rust:
q = mg / E
Als we de dichtheid en straal van de druppel kennen, wordt de massa van de druppel bepaald:
ρ = m / V
V = (4/3) πR3
Daarom:
m ρ.V = ρ. (4/3) πR3 927 kg / m3. (4/3) π. (4,37 x 10-7 m)3= 3,24 x 10-16 kg
Daarom is de lading van de druppel:
q = mg / E = 3,24 x 10-16 kg x 9,8 m / stwee/ 9660 N = 3,3 x 10-19 C
Oplossing b
Wetende dat de fundamentele lading e = 1,6 x 10 is -19 C, de belasting verkregen in de vorige sectie wordt gedeeld door deze waarde:
n = q / e = 3,3 x 10-19 C /1,6 x 10 -19 C = 2,05
Het resultaat is dat de lading op de druppel ongeveer tweemaal (n≈2) de elementaire lading is. Het is niet precies het dubbele, maar deze kleine discrepantie is te wijten aan de onvermijdelijke aanwezigheid van experimentele fouten, evenals afrondingen in elk van de voorgaande berekeningen..
Oplossing c
Het is mogelijk om het teken van de lading te bepalen, dankzij het feit dat de verklaring informatie geeft over de richting van het veld, dat verticaal naar boven is gericht, evenals de kracht.
Elektrische veldlijnen beginnen altijd met positieve ladingen en eindigen met negatieve ladingen, daarom wordt de onderste plaat geladen met een + teken en de bovenste plaat met een - teken (zie figuur 3).
Omdat de druppel is gericht naar de plaat erboven aangedreven door het veld, en aangezien ladingen van tegengesteld teken aantrekken, moet de druppel een positieve lading hebben.
In werkelijkheid is het niet eenvoudig om de druppel hangend te houden. Dus gebruikte Millikan de verticale verplaatsingen (ups en downs) die de druppel ervoer door het veld uit en weer in te schakelen, plus de veranderingen in röntgenlading en reistijden, om te schatten hoeveel extra lading de druppel had gekregen..
Deze verworven lading is evenredig met de lading van het elektron, zoals we al hebben gezien, en kan worden berekend met de stijg- en daaltijden, de massa van de druppel en de waarden van g Y EN.
Referenties
- Open geest. Millikan, de fysicus die het elektron kwam bekijken. Hersteld van: bbvaopenmind.com
- Rex, A. 2011. Fundamentals of Physics. Pearson.
- Tippens, P. 2011. Fysica: concepten en toepassingen. 7e editie. Mcgraw heuvel.
- Amrita. Millikan's oliedruppel-experiment. Teruggeplaatst van: vlab.amrita.edu
- Wake Forest College. Millikan's oliedruppel-experiment. Hersteld van: wfu.edu



Niemand heeft nog op dit artikel gereageerd.