
Constante functiekenmerken, voorbeelden, oefeningen
De constante functie is degene waarin de waarde van y constant wordt gehouden. Met andere woorden: een constante functie heeft altijd de vorm f (x) = k, waar k is een reëel getal.
Bij het plotten van de constante functie in het coördinatensysteem xy, resulteert altijd in een rechte lijn evenwijdig aan de horizontale as of as van de X.
Deze functie is een specifiek geval van de affiene functie, waarvan de grafiek ook een rechte lijn is, maar met een helling. De constante functie heeft een helling van nul, dat wil zeggen, het is een horizontale lijn, zoals weergegeven in figuur 1.
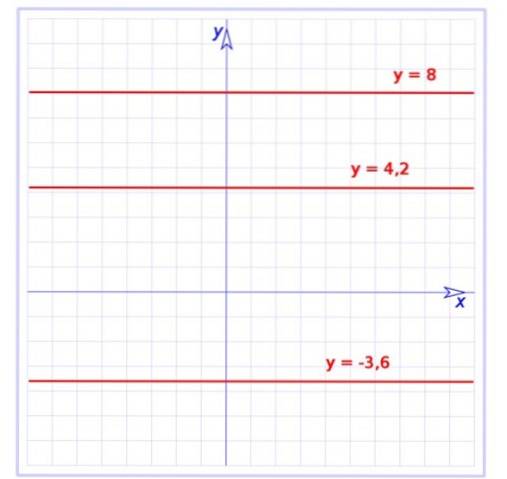
Daar wordt de grafiek van drie constante functies getoond:
f (x) = -3,6
g (x) = 4,2
h (x) = 8
Het zijn allemaal lijnen evenwijdig aan de horizontale as, de eerste bevindt zich onder de as, terwijl de rest erboven is.
Artikel index
- 1 Kenmerken van de constante functie
- 2 voorbeelden
- 2.1 Een andere manier om een constante functie weer te geven
- 3 Opgeloste oefeningen
- 3.1 - Oefening 1
- 3.2 - Oefening 2
- 3.3 - Oefening 3
- 3.4 - Oefening 4
- 3.5 - Oefening 6
- 4 referenties
Kenmerken van de constante functie
We kunnen de belangrijkste kenmerken van de constante functie als volgt samenvatten:
-De grafiek is een rechte horizontale lijn.
-Het heeft een enkele kruising met de as Y, waard k.
-Is continu.
-Het domein van de constante functie (de set waarden die het X) is de verzameling reële getallen R.
-Het pad, bereik of tegendomein (de set waarden die de variabele aanneemt Y) is gewoon de constante k.
Voorbeelden
Functies zijn nodig om verbanden te leggen tussen hoeveelheden die op de een of andere manier van elkaar afhankelijk zijn. De relatie tussen hen kan wiskundig worden gemodelleerd om erachter te komen hoe een van hen zich gedraagt wanneer de andere varieert..
Dit helpt om modellen te bouwen voor veel situaties en voorspellingen te doen over hun gedrag en evolutie..
Ondanks zijn schijnbare eenvoud kent de constante functie vele toepassingen. Bijvoorbeeld als het gaat om het bestuderen van grootheden die constant blijven in de tijd, of in ieder geval gedurende een aanzienlijke tijd.
Op deze manier gedragen magnitudes zich in situaties als de volgende:
-De snelheid cruisen met een auto die over een lange rechte snelweg rijdt. Zolang je niet remt of accelereert, heeft de auto een gelijkmatige rechtlijnige beweging.

-Een volledig opgeladen condensator die is losgekoppeld van een circuit heeft een laden constant in de tijd.
-Ten slotte onderhoudt een parkeerplaats met een vast tarief een prijs constant, ongeacht hoe lang een auto daar geparkeerd staat.
Een andere manier om een constante functie weer te geven
De constante functie kan ook als volgt worden weergegeven:
f (x) = kx0
Aangezien elke waarde van X verheven tot 0 geeft 1 als resultaat, de vorige uitdrukking reduceert tot de reeds bekende:
f (x) = k
Dat gebeurt natuurlijk zolang de waarde van k is anders dan 0.
Daarom wordt de constante functie ook geclassificeerd als een polynoom functie van graad 0, sinds de exponent van de variabele X is 0.
Opgeloste oefeningen
- Oefening 1
Beantwoord de volgende vragen:
a) Kan worden gesteld dat de regel gegeven door x = 4 een constante functie is? Reden voor uw antwoord.
b) Kan een constante functie een x-snijpunt hebben?
c) Is de functie f (x) = w constanttwee?
Antwoord op
Hier is de grafiek van de lijn x = 4:
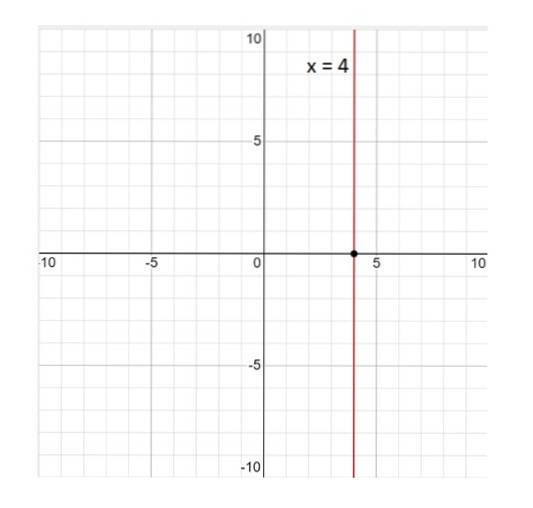
De regel x = 4 is geen functie; per definitie is een functie een relatie zodanig dat bij elke waarde van de variabele X komt overeen met een enkele waarde van Y. En in dit geval is dit niet waar, aangezien de waarde x = 4 wordt geassocieerd met oneindige waarden van Y. Daarom is het antwoord nee.
Antwoord b
Over het algemeen heeft een constante functie geen snijpunt met de as X, tenzij het ongeveer is y = 0, in dat geval is het de as X Goed gezegd.
Antwoord c
Ja, sinds w is constant, net als het kwadraat. Het gaat erom dat w niet afhankelijk van invoervariabele X.
- Oefening 2
Zoek de kruising tussen de functies f (x) = 5 Y g (x) = 5x - 2
Oplossing
Om het snijpunt tussen deze twee functies te vinden, kunnen ze respectievelijk worden herschreven als:
y = 5; y = 5x - 2
Ze worden vereffend en krijgen:
5x - 2 = 5
Wat is een lineaire vergelijking van de eerste graad, waarvan de oplossing is:
5x = 5 + 2 = 7
x = 7/5
Het snijpunt is (7 / 5,5).
- Oefening 3
Laat zien dat de afgeleide van een constante functie 0 is.
Oplossing
Van de definitie van afgeleide hebben we:

f (x + h) = k
Vervanging in de definitie:

Ook als we de afgeleide beschouwen als de snelheid van verandering dy / dx, de constante functie ondergaat geen enkele verandering, daarom is zijn afgeleide nul.
- Oefening 4
Vind de onbepaalde integraal van f (x) = k.
Oplossing

Een gsm-bedrijf biedt een onbeperkte internetservice tegen een vast tarief voor $ 15 per maand. Wat is de prijsfunctie volgens de tijd?
Oplossing
Laat P de te betalen prijs zijn in $ en t de tijd, die kan worden uitgedrukt in dagen. De functie is als volgt ingesteld:
P (t) = 15
- Oefening 6
De volgende grafiek van snelheid versus tijd komt overeen met de beweging van een deeltje.

Het vraagt:
a) Schrijf een uitdrukking voor de snelheidsfunctie als functie van de tijd v (t).
b) Zoek de afstand die de gsm heeft afgelegd in het tijdsinterval tussen 0 en 9 seconden.
Oplossing voor
Uit de weergegeven grafiek blijkt dat:
-v = 2 m / s in het tijdsinterval tussen 0 en 3 seconden
-De mobiel wordt gestopt tussen 3 en 5 seconden, omdat in dit interval de snelheid 0 is.
-v = - 3 m / s tussen 5 en 9 seconden.
Het is een voorbeeld van een stuksgewijze functie, of stuksgewijze functie, die op zijn beurt is samengesteld uit constante functies die alleen geldig zijn voor de aangegeven tijdsintervallen. Geconcludeerd wordt dat de gezochte functie is:

Oplossing b
Uit de v (t) -grafiek kan de door de mobiel afgelegde afstand worden berekend, die numeriek equivalent is aan het gebied onder / op de curve. Op deze manier:
-Afgelegde afstand tussen 0 en 3 seconden = 2 m / s. 3 s = 6 m
-Tussen 3 en 5 seconden werd hij gestopt, daarom heeft hij geen afstand afgelegd.
-Afgelegde afstand tussen 5 en 9 seconden = 3 m / s. 4 s = 12 m
In totaal heeft de mobiel 18 meter afgelegd. Merk op dat hoewel de snelheid negatief is in het interval tussen 5 en 9 seconden, de afgelegde afstand positief is. Wat er gebeurt, is dat de mobiele telefoon tijdens dat tijdsinterval het gevoel van zijn snelheid had veranderd.
Referenties
- Geogebra. Constante functies. Hersteld van: geogebra.org.
- Maplesoft. De constante functie. Hersteld van: maplesoft.com.
- Wikibooks. Berekening in een variabele / Functies / Constante functie. Hersteld van: es.wikibooks.org.
- Wikipedia. Constante functie. Hersteld van: en.wikipedia.org
- Wikipedia. Constante functie. Hersteld van: es.wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.