Logaritmische functie-eigenschappen, voorbeelden, oefeningen

De logaritmische functie is een wiskundige relatie die elk positief reëel getal associeert X met zijn logaritme Y op een basis naar. Deze relatie voldoet aan de eisen om een ​​functie te zijn: elk element x behorend bij het domein heeft een unieke afbeelding.

Daarom:

f (x) = y = logboek_naar X , met een> 0 en verschillend van 1.

De belangrijkste eigenschappen van de logaritmische functie zijn:

-Het domein is allemaal reëel groter dan 0, exclusief 0. Met andere woorden, er is geen logaritme van 0 of negatieve getallen in een grondtal. In intervalvorm:

Zon _F. = (0, ∞ +)

-De logaritme van een getal kan negatief, positief of 0 zijn, dus het bereik of bereik is:

Rgo _F. = (-​ +)

-De logaritmische functie neemt altijd toe voor a> 1 en afnemend voor a<1.

-Het omgekeerde van f (x) = logboek_naar X is de exponentiële functie.

Inderdaad, de logaritmefunctie gebaseerd op, is de inverse functie van de potentiële functie:

F.^-1(x) = een^Y

Omdat de logaritme in base naar van een nummer X, Het is het nummer Y waarnaar de basis moet worden verhoogd naar krijgen X.

-De logaritme van de basis is altijd 1. Dus de grafiek van f (x) = logboek_naar X snijdt altijd de x-as op het punt (1,0)

-De logaritmische functie is transcendent en het kan niet worden uitgedrukt als een polynoom of als een quotiënt hiervan. Naast de logaritme omvat deze groep onder meer de trigonometrische en exponentiële functies.

Artikel index

• 1 Voorbeelden
• 2 De voordelen van logaritmen
  • 2.1 Voorbeeld
• 3 Toepassingsoefening: de schaal van Richter
  • 3.1 Oplossing
• 4 referenties

Voorbeelden

De logaritmische functie kan worden bepaald door verschillende grondslagen, maar de meest gebruikte zijn 10 en en, waar en is het Eulergetal gelijk aan 2,71828 ... .

Wanneer de grondtal 10 wordt gebruikt, wordt de logaritme een decimale logaritme, vulgaire logaritme, Briggs of gewoon logaritme genoemd.

En als het getal e wordt gebruikt, wordt het een natuurlijke logaritme genoemd, door John Napier, de Schotse wiskundige die logaritmen ontdekte..

De notatie die voor elk wordt gebruikt, is de volgende:

-Decimale logaritme: log₁₀ x = logboek x

-Natuurlijke logaritme: ln x

Wanneer een ander grondtal moet worden gebruikt, is het absoluut noodzakelijk om dit als een subscript aan te duiden, omdat de logaritme van elk nummer verschilt afhankelijk van de te gebruiken basis. Als het bijvoorbeeld logaritmen zijn in grondtal 2, schrijft u:

y = logboek_twee X

Laten we eens kijken naar de logaritme van het getal 10 in drie verschillende bases, om dit punt te illustreren:

logboek 10 = 1

ln 10 = 2,30259

logboek_twee 10 = 3,32193

Gewone rekenmachines brengen alleen decimale logaritmen (logfunctie) en natuurlijke logaritme (ln-functie). Op internet zijn er rekenmachines met andere bases. In elk geval kan de lezer met zijn hulp verifiëren dat de bovenstaande waarden waar zijn:

10¹ = 10

en^2.306 = 10.0001

twee^3.32193 = 10.0000

Kleine decimale verschillen zijn te wijten aan het aantal decimalen dat wordt gebruikt bij het berekenen van de logaritme.

De voordelen van logaritmen

Een van de voordelen van het gebruik van logaritmen is het gemak dat ze bieden om met grote getallen te werken, door hun logaritme te gebruiken in plaats van het nummer rechtstreeks.

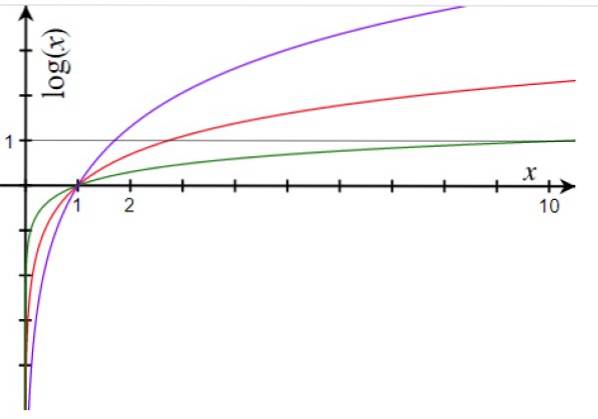
Dit is mogelijk omdat de logaritmefunctie langzamer groeit naarmate de getallen groter worden, zoals we in de grafiek kunnen zien.

Dus zelfs bij zeer grote getallen zijn hun logaritmen veel kleiner en is het manipuleren van kleine getallen altijd gemakkelijker..

Bovendien hebben logaritmen de volgende eigenschappen:

-Product: log (a.b) = log a + log b

-Quotiënt: log (a / b) = log a - log b

-Kracht: log een^b = b.log een

En op deze manier worden de producten en quotiënten optellingen en aftrekkingen van kleinere getallen, terwijl de potentiëring een eenvoudig product wordt, ook al is het vermogen hoog..

Dat is de reden waarom logaritmen ons in staat stellen getallen uit te drukken die variëren in zeer grote waardenbereiken, zoals de intensiteit van geluid, de pH van een oplossing, de helderheid van sterren, de elektrische weerstand en de intensiteit van aardbevingen op de schaal van Richter..

Laten we eens kijken naar een voorbeeld van de afhandeling van de eigenschappen van logaritmen:

Voorbeeld

Zoek de waarde van x in de volgende uitdrukking:

logboek (5x +1) = 1 + logboek (2x-1)

Antwoord

We hebben hier een logaritmische vergelijking, aangezien het onbekende in het argument van de logaritme zit. Het wordt opgelost door een enkele logaritme aan elke kant van de gelijkheid achter te laten.

We beginnen met het plaatsen van alle termen die "x" bevatten aan de linkerkant van de gelijkheid, en degene die alleen cijfers bevatten aan de rechterkant:

logboek (5x + 1) - logboek (2x-1) = 1

Aan de linkerkant hebben we de aftrekking van twee logaritmen, die kunnen worden geschreven als de logaritme van een quotiënt:

log [(5x + 1) / (2x-1)] = 1

Aan de rechterkant is echter het nummer 1, dat we kunnen uitdrukken als log 10, zoals we eerder zagen. Dan:

log [(5x + 1) / (2x-1)] = log 10

Om gelijkheid te vervullen, argumenten van de logaritmen moet gelijk zijn:

(5x + 1) / (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Toepassingsoefening: de schaal van Richter

In 1957 vond er een aardbeving plaats in Mexico met een kracht van 7,7 op de schaal van Richter. In 1960 deed zich in Chili nog een aardbeving van grotere omvang voor, namelijk 9,5.

Bereken hoe vaak de aardbeving in Chili heviger was dan die in Mexico, wetende dat de omvang M_R op de schaal van Richter wordt het gegeven door de formule:

M._R = logboek (10⁴ IK)

Oplossing

De omvang van een aardbeving op de schaal van Richter is een logaritmische functie. We gaan de intensiteit van elke aardbeving berekenen, aangezien we de magnitudes van Richter hebben. Laten we het stap voor stap doen:

-Mexico: 7.7 = logboek (10⁴ IK)

Omdat de inverse van de logaritmefunctie de exponentiële is, passen we dit toe op beide zijden van de gelijkheid met de bedoeling I op te lossen, wat gevonden wordt in het argument van de logaritme.

Omdat het decimale logaritmen zijn, is het grondtal 10. Dan:

10 ^7.7 = 10⁴ ik

De intensiteit van de aardbeving in Mexico was:

ik_M. = 10 ^7.7 / 10⁴ = 10^3.7

 -Chili: 9.5 = logboek (10⁴ IK)

Dezelfde procedure brengt ons bij de intensiteit van de Chileense aardbeving I_Ch​

ik_Ch = 10 ^9.5 / 10⁴ = 10^5.5

 Nu kunnen we beide intensiteiten vergelijken:

ik_Ch / Ik_M. = 10^5.5 / 10^3.7 = 10^1.8 = 63,1

 ik_Ch = 63,1. ik_M.

De aardbeving in Chili was ongeveer 63 keer heviger dan die in Mexico. Omdat de magnitude logaritmisch is, groeit deze langzamer dan de intensiteit, dus een verschil van 1 in de magnitude betekent een 10 keer grotere amplitude van de seismische golf.

Het verschil tussen de magnitudes van beide aardbevingen is 1,8, daarom konden we een verschil in intensiteit verwachten dat dichter bij 100 ligt dan bij 10, zoals het werkelijk gebeurde..

Als het verschil precies 2 was geweest, zou de Chileense aardbeving 100 keer intenser zijn geweest dan de Mexicaanse..

Referenties

1. Carena, M. 2019. Pre-University Mathematics Manual. Nationale Universiteit van de Litoral.
2. Figuera, J. 2000. Wiskunde 1e. Gediversifieerd jaar. CO-BO edities.
3. Jiménez, R. 2008. Algebra. Prentice hal.
4. Larson, R. 2010. Berekening van een variabele. 9e. Editie. Mcgraw heuvel.
5. Stewart, J. 2006. Precalculus: wiskunde voor calculus. 5e. Editie. Cengage leren.