
Inverse trigonometrische functies waarde, afgeleiden, voorbeelden, oefeningen
De inverse trigonometrische functies, Zoals de naam al aangeeft, zijn het de overeenkomstige inverse functies van de sinus-, cosinus-, tangens-, cotangens-, secans- en cosecansfuncties..
Inverse trigonometrische functies worden aangeduid met dezelfde naam als hun overeenkomstige directe trigonometrische functie plus het voorvoegsel boog. Dus:
1.- arcsen (x) is de inverse trigonometrische functie van de functie sen (x)
twee.- arccos (x) is de inverse trigonometrische functie van de functie cos (x)
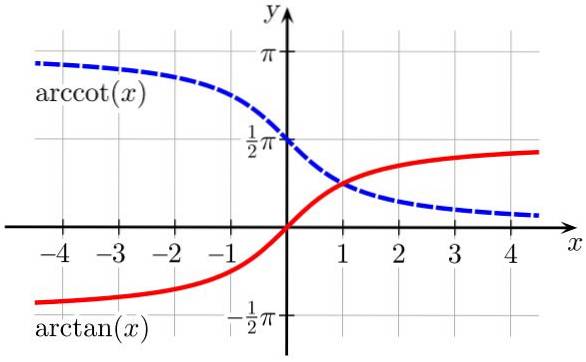
3.- arctan (x) is de inverse trigonometrische functie van de functie dus (x)
4.- arccot (x) is de inverse trigonometrische functie van de functie kinderbed (x)
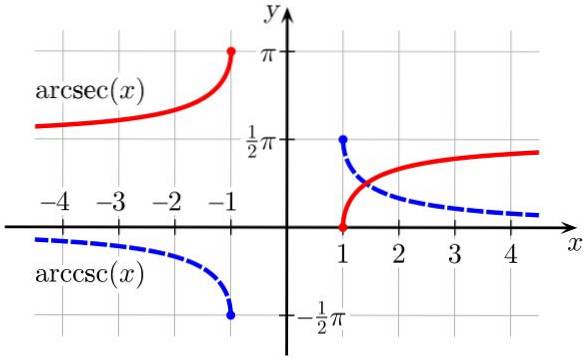
5.- boogseconden (x) is de inverse trigonometrische functie van de functie sec (x)
6.- arccsc (x) is de inverse trigonometrische functie van de functie csc (x)
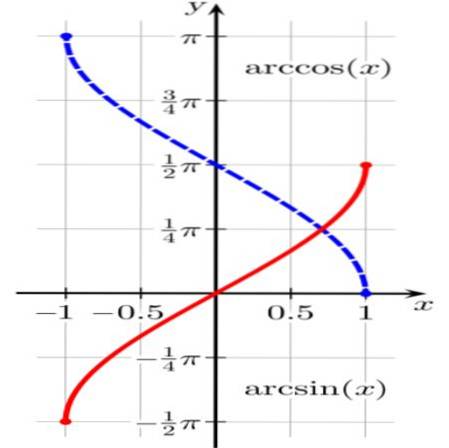
De functie θ = arcsen (x) resulteert in een eenheidsboog θ (of hoek in radialen θ) zoals dat zonde (θ) = x.
Dus bijvoorbeeld arcsen (√3 / 2) = π / 3 aangezien, zoals bekend, de sinus van π / 3 radialen gelijk is aan √3 / 2.
Artikel index
- 1 Hoofdwaarde van inverse trigonometrische functies
- 1.1 Tabel met domeinen en bereiken van inverse trigonometrische functies
- 2 Afgeleiden van inverse trigonometrische functies
- 3 voorbeelden
- 3.1 - Voorbeeld 1
- 3.2 - Voorbeeld 2
- 4 oefeningen
- 4.1 - Oefening 1
- 4.2 - Oefening 2
- 4.3 - Oefening 3
- 5 referenties
Hoofdwaarde van inverse trigonometrische functies
Wil een wiskundige functie f (x) een inverse hebben g (x) = f-1(x) het is noodzakelijk dat deze functie injectief, wat betekent dat elke waarde y van de aankomstset van de functie f (x) afkomstig is van één en slechts één waarde x.
Het is duidelijk dat aan deze eis door geen enkele trigonometrische functie wordt voldaan. Om het punt te verduidelijken, merk op dat de waarde y = 0,5 kan worden verkregen uit de sinusfunctie op de volgende manieren:
- sin (π / 6) = 0,5
- sin (5π / 6) = 0,5
- sin (7π / 6) = 0,5
En nog veel meer, aangezien de sinusfunctie periodiek is met periode 2π.
Om de inverse trigonometrische functies te definiëren, is het noodzakelijk om het domein van hun overeenkomstige directe trigonometrische functies te beperken, zodat ze voldoen aan de injectiviteitsvereiste.
Dat beperkte domein van de directe functie zal het bereik of de hoofdtak zijn van de overeenkomstige inverse functie.
Tabel met domeinen en bereiken van inverse trigonometrische functies

Afgeleiden van inverse trigonometrische functies
Om de afgeleiden van de inverse trigonometrische functies te verkrijgen, worden de eigenschappen van de afgeleiden toegepast, in het bijzonder de afgeleide van een inverse functie.
Als we de functie met f (y) aangeven en met f-1(x) naar zijn inverse functie, dan is de afgeleide van de inverse functie gerelateerd aan de afgeleide van de directe functie door de volgende relatie:
[F.-1(x)] '= 1 / f' [f-1(X)]
Bijvoorbeeld: als x = f (y) = √y de directe functie is, zal het omgekeerde zijn
y = f-1(x) = xtwee. Laten we de regel van de afgeleide van de inverse toepassen op dit eenvoudige geval om te zien of aan deze regel is voldaan:
[Xtwee] '= 1 / [√y]' = 1 / (½ j-½ = 2 en½ = 2 (xtwee½ = 2x
We kunnen deze truc gebruiken om de afgeleiden van de inverse trigonometrische functies te vinden.
We nemen bijvoorbeeld θ = arcsen (x) als de directe functie, dan zal de inverse functie zijn zonde (θ) = x.
[arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sin (θ)twee
... = 1 / √ (1 - xtwee .
Op deze manier kunnen alle afgeleiden van de inverse trigonometrische functies worden verkregen, die hieronder worden weergegeven:

Deze afgeleiden zijn geldig voor elk argument z behorende tot de complexe getallen en daarom zijn ze ook geldig voor elk reëel argument x, aangezien z = x + 0i.
Voorbeelden
- voorbeeld 1
Vind arctan (1).
Oplossing
De arctan (1) is de eenheidsboog (hoek in radialen) ፀ zodat tan (ፀ) = 1. Die hoek is ፀ = π / 4 omdat tan (π / 4) = 1. Dus arctan (1) = π / 4.
- Voorbeeld 2
Bereken arcsen (cos (π / 3)).
Oplossing
De hoek π / 3 radialen is een opmerkelijke hoek waarvan de cosinus ½ is, dus het probleem komt neer op het vinden van arcsen (½).
Dan is het een kwestie van uitzoeken wat de hoek is waarvan de sinus ½ geeft. Die hoek is π / 6, aangezien sin (π / 6) = sin (30º) = ½. Daarom arcsen (cos (π / 3)) = π / 6.
Opleiding
- Oefening 1
Zoek het resultaat van de volgende uitdrukking:
sec (arctan (3)) + csc (arccot (4))
Oplossing
We beginnen met de naam α = arctan (3) en β = arccot (4). Dan ziet de uitdrukking die we moeten berekenen er als volgt uit:
sec (α) + csc (β)
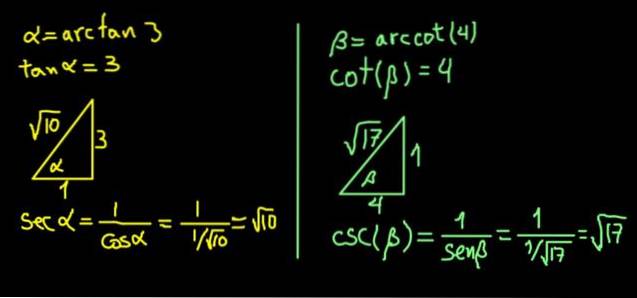
De uitdrukking α = arctan (3) is gelijk aan tan (α) = 3.
Omdat de raaklijn het tegenoverliggende been is boven het aangrenzende been, construeren we een rechthoekige driehoek met een been tegenover α van 3 eenheden en een aangrenzend been van 1 eenheid, zodat tan (α) = 3/1 = 3.
In een rechthoekige driehoek wordt de hypotenusa bepaald door de stelling van Pythagoras. Met deze waarden is het resultaat √10, zodat:
sec (α) = hypotenusa / aangrenzend been = √10 / 1 = √10.
Evenzo is β = arccot (4) gelijk aan bevestigen dat wieg (β) = 4.
We construeren een rechterpootdriehoek naast β van 4 eenheden en een tegenoverliggende poot van 1 eenheid, zodat wieg (β) = 4/1.
De driehoek wordt onmiddellijk voltooid door de hypotenusa te vinden dankzij de stelling van Pythagoras. In dit geval bleek het √17 eenheden te hebben. Vervolgens wordt de csc (β) = hypotenusa / tegenovergestelde poot = √17 / 1 = √17 berekend.
Onthoud dat de uitdrukking die we moeten berekenen is:
sec (arctan (3)) + csc (arccot (4)) = sec (α) + csc (β) =…
… = √10 + √17 = 3,16 + 4,12 = 7,28.
- Oefening 2
Vind de oplossingen van:
Cos (2x) = 1 - Sen (x)

Oplossing
Het is noodzakelijk dat alle trigonometrische functies worden uitgedrukt in hetzelfde argument of dezelfde hoek. We zullen de identiteit van de dubbele hoek gebruiken:
Cos (2x) = 1-2 sentwee(X)
Vervolgens wordt de oorspronkelijke uitdrukking teruggebracht tot:
1 - 2 Sentwee(x) = 1 - Sen x
Eenmaal vereenvoudigd en ingecalculeerd, wordt het uitgedrukt als:
zonde (x) (2 sin (x) - 1) = 0
Dat geeft aanleiding tot twee mogelijke vergelijkingen: Sen (x) = 0 met oplossing x = 0 en nog een vergelijking sin (x) = ½ met x = π / 6 als oplossing.
De oplossingen voor de vergelijking zijn: x = 0 of x = π / 6.
- Oefening 3
Vind de oplossingen van de volgende goniometrische vergelijking:
cos (x) = zondetwee(X)
Oplossing
Om deze vergelijking op te lossen is het handig om slechts één type trigonometrische functie te plaatsen, dus we zullen de fundamentele trigonometrische identiteit gebruiken zodat de oorspronkelijke vergelijking als volgt wordt herschreven:
cos (x) = 1 - costwee(X)
Als we y = cos (x) noemen, kan de uitdrukking worden herschreven als:
Ytwee + en - 1 = 0
Het is een vergelijking van de tweede graad in y, waarvan de oplossingen zijn:
y = (-1 ± √5) / 2
Dan zijn de waarden van x die voldoen aan de oorspronkelijke vergelijking:
x = arccos ((-1 ± √5) / 2)
De echte oplossing is die met een positief teken x = 0,9046 rad = 51,83º.
De andere oplossing is complex: x = (π - 1,06 i) rad.
Referenties
- Hazewinkel, M. 1994. Encyclopedie van de wiskunde. Kluwer Academic Publishers / Springer Science & Business Media.
- Mate Mobile. Inverse goniometrische functies. Hersteld van: matemovil.com
- Universum-formules. Inverse goniometrische functies. Hersteld van: universoformulas.com
- Weisstein, Eric W. Inverse trigonometrische functies. Hersteld van: mathworld.wolfram.com
- Wikipedia. Inverse goniometrische functies. Hersteld van: en.wikipedia.com


Niemand heeft nog op dit artikel gereageerd.