
Ideaal gasmodel, gedrag, voorbeelden
EEN Ideaal gas of perfect gas Het is er een waarin de moleculaire aantrekkingskracht of afstotingskracht tussen de deeltjes waaruit het bestaat, als onbeduidend wordt beschouwd, daarom is al zijn interne energie kinetisch, dat wil zeggen energie geassocieerd met beweging.
In een dergelijk gas staan de deeltjes meestal vrij ver uit elkaar, hoewel ze van tijd tot tijd met elkaar en met de wanden van de container in botsing komen..
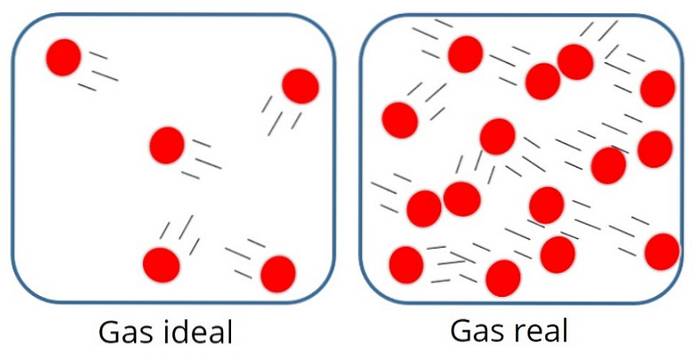
Aan de andere kant zijn in het ideale gas noch de grootte, noch de massa van de deeltjes van belang, aangezien wordt aangenomen dat het volume dat erdoor wordt ingenomen erg klein is in vergelijking met het volume van het gas zelf..
Dit is natuurlijk slechts een benadering, want in werkelijkheid is er altijd een zekere mate van interactie tussen atomen en moleculen. We weten ook dat deeltjes ruimte innemen en massa hebben..
Deze aannames werken in veel gevallen echter vrij goed, zoals gassen met een laag molecuulgewicht, bij een goed bereik van drukken en temperaturen..
Gassen met een hoog molecuulgewicht, vooral bij hoge drukken of lage temperaturen, gedragen zich echter helemaal niet als ideale gassen en er zijn andere modellen nodig die zijn gemaakt om ze nauwkeuriger te beschrijven..
Artikel index
- 1 Eerste experimenten
- 1.1 De ideale gaswetten
- 2 Ideaal gasmodel
- 2.1 Ideale gasstatusvergelijking
- 2.2 De gasconstante
- 3 Gedrag van een ideaal gas
- 4 Voorbeelden van ideale gassen
- 4.1 Edelgassen
- 4.2 De heteluchtballon
- 4.3 Heliumballonnen
- 5 referenties
Eerste experimenten
De wetten die gassen regelen, zijn empirisch, dat wil zeggen, ze zijn voortgekomen uit experimenten. De meest opmerkelijke experimenten werden uitgevoerd in de zeventiende, achttiende en vroege negentiende eeuw.
De eerste zijn die van Robert Boyle (1627-1691) en Edme Mariotte (1620-1684), die onafhankelijk de Druk in een gas en registreerde de verandering van volume, constateren dat ze omgekeerd evenredig waren: hoe hoger de druk, hoe kleiner het volume.

Jacques Charles (1746-1823) stelde van zijn kant vast dat het volume en temperatuur- absolute waarden waren recht evenredig, zolang de druk constant bleef.
Amadeo Avogadro (1776-1856) ontdekte dat twee identieke volumes van verschillende gassen hetzelfde aantal deeltjes bevatten, zolang de druk en temperatuur maar hetzelfde waren. En tot slot stelde Joseph de Gay Lussac (1778-1850) dat door het volume vast te houden, de druk in een gas recht evenredig is met de temperatuur..
De ideale gaswetten
Deze ontdekkingen worden uitgedrukt in eenvoudige formules, roepen p onder druk, V. naar volume, n naar het aantal deeltjes en T de ideale gastemperatuur:
Boyle-Mariotte wet
Zolang de temperatuur vaststaat, gebeurt het volgende:
p⋅V = constant
Charles Law
Als het gas constant onder druk staat:
V / T = constant
De wet van Gay Lussac
Door het gas op een vast volume te houden, is voldaan aan het volgende:
p / T = constant
De wet van Avogadro
Identieke gasvolumes, onder dezelfde druk- en temperatuuromstandigheden, hebben hetzelfde aantal deeltjes. Daarom kunnen we schrijven:
V ∝ n
Waarbij n het aantal deeltjes is en ∝ het symbool van evenredigheid.
Ideaal gasmodel
Het ideale gasmodel beschrijft een gas zodanig dat:
-Wanneer de deeltjes op elkaar inwerken, doen ze dat voor een zeer korte tijd, door middel van elastische botsingen, waarbij momentum en kinetische energie behouden blijven..
-De samenstellende deeltjes zijn punctueel, met andere woorden, hun diameter is veel kleiner dan de gemiddelde afstand die ze afleggen tussen de ene botsing en de andere..
-Intermoleculaire krachten zijn niet aanwezig.
-Kinetische energie is evenredig met de temperatuur.
Monatomische gassen - waarvan de atomen niet aan elkaar zijn gebonden - en een laag molecuulgewicht, onder standaard omstandigheden van druk en temperatuur (atmosferische druk en 0ºC temperatuur), vertonen een zodanig gedrag dat het ideale gasmodel een zeer goede omschrijving voor hen is..
Ideale gasstatusvergelijking
De bovenstaande gaswetten vormen samen de algemene vergelijking die het gedrag van het ideale gas bepaalt:
V ∝ n
V ∝ T
Daarom:
V ∝ n⋅T
Ook uit de wet van Boyle:
V = constant / p
Dus we kunnen bevestigen dat:
V = (constante x n⋅T) / p
De constante wordt de gas constant en wordt aangeduid met de letter R.Met deze keuze heeft de ideale gasvergelijking van toestand betrekking op vier variabelen die de toestand van het gas beschrijven, namelijk n, R, p en T, waarbij het volgende overblijft:
p⋅V = n⋅R⋅T
Deze relatief eenvoudige vergelijking is consistent met de ideale gaswetten. Als de temperatuur bijvoorbeeld constant is, wordt de vergelijking gereduceerd tot de wet van Boyle-Mariotte.
Het gas constant
Zoals we eerder hebben gezegd, onder standaardomstandigheden van temperatuur en druk, dat wil zeggen bij 0 ° C (273,15 K) en 1 atmosfeer druk, is het gedrag van veel gassen dicht bij dat van het ideale gas. Onder deze omstandigheden is het volume van 1 mol gas 22.414 L.
In dat geval:
R = (p⋅V) / (n⋅T) = (1 atm x 22,414 L) / (1 mol x 273,15 K) = 0,0821 atm ⋅ L / mol ⋅ K
De gasconstante kan ook worden uitgedrukt in andere eenheden, bijvoorbeeld in het SI International System is het de moeite waard:
R = 8,314 J⋅ mol-1⋅ K-1
Bij het oplossen van een probleem met behulp van de ideale gaswet, is het handig om aandacht te besteden aan de eenheden waarin de constante wordt uitgedrukt, omdat zoals we kunnen zien, er veel mogelijkheden zijn.
Gedrag van een ideaal gas
Zoals we hebben gezegd, gedraagt elk gas onder standaardomstandigheden van druk en temperatuur en dat een laag molecuulgewicht heeft, zich zeer dicht bij het ideale gas. Daarom is de vergelijking p⋅V = n⋅R⋅T van toepassing om het verband te vinden tussen de vier variabelen die het beschrijven: n, p, V en T.
Op deze manier kunnen we ons een portie ideaal gas voorstellen dat is ingesloten in een container en wordt gevormd door kleine deeltjes, die van tijd tot tijd met elkaar en met de wanden van de container botsen, altijd elastisch..
Dit is wat we zien in de volgende animatie van een deel van helium, een mono-atomisch edelgas:
Voorbeelden van ideale gassen
Een ideaal gas is een hypothetisch gas, dat wil zeggen, het is een idealisatie, maar in de praktijk gedragen veel gassen zich zeer nauw, waardoor het model p⋅V = n⋅R arroT zeer goede resultaten kan geven..
Edele gassen
Voorbeelden van gassen die zich onder standaardomstandigheden als ideaal gedragen, zijn edelgassen, maar ook lichte gassen: waterstof, zuurstof en stikstof..
De aerostatische ballon

De wet van Charles kan worden toegepast op de heteluchtballon in figuur 1: het gas warmt op, daarom zet de lucht die de ballon vult uit en als gevolg daarvan stijgt het op.
Helium ballonnen
Helium is, samen met waterstof, het meest voorkomende element in het universum, en toch is het zeldzaam op aarde. Omdat het een edelgas is, is het inert, in tegenstelling tot waterstof, daarom worden met helium gevulde ballonnen veel gebruikt als decoratieve elementen..
Referenties
- Atkins, P. 1999. Physical Chemistry. Omega-edities.
- Chang, R. 2013. Chemistry. 11e. Editie. Mc Graw Hill Education.
- Cengel, Y. 2012. Thermodynamica. 7e editie. Mcgraw heuvel.
- Cimbala, C. 2006. Vloeistofmechanica, grondbeginselen en toepassingen. Mc. Graw Hill.
- Giambattista, A. 2010. Physics. 2e. Ed McGraw Hill.



Niemand heeft nog op dit artikel gereageerd.