
Demonstratie van Pythagorische identiteiten, voorbeelden, oefeningen
Zij zijn Pythagorische identiteiten alle trigonometrische vergelijkingen die gelden voor elke waarde van de hoek en zijn gebaseerd op de stelling van Pythagoras. De bekendste van de Pythagorische identiteiten is de fundamentele trigonometrische identiteit:
Sentwee(α) + Costwee(α) = 1
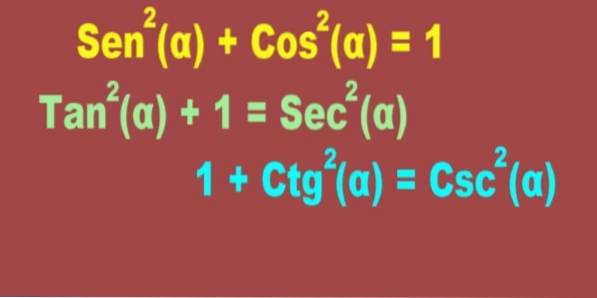
Volgende in belangrijkheid en ik gebruik de Pythagorische identiteit van de tangens en secans:
Zotwee(α) + 1 = Sectwee(α)
En de goniometrische identiteit van Pythagoras met de cotangens en de cosecans:
1 + Ctgtwee(α) = Csctwee(α)
Artikel index
- 1 demo
- 1.1 De sinus en cosinus
- 1.2 De fundamentele identiteit
- 1.3 De raaklijn
- 1.4 De Pythagorische identiteit van de raaklijn
- 2 Voorbeeld
- 3 Opgeloste oefeningen
- 3.1 Oefening 1
- 3.2 Oefening 2
- 4 referenties
Demonstratie
De trigonometrische verhoudingen borst Y cosinus ze worden weergegeven in een cirkel met straal één (1), bekend als een trigonometrische cirkel. Deze cirkel heeft het middelpunt bij de oorsprong van coördinaten O.
De hoeken worden gemeten vanaf de positieve halve as van de X, bijvoorbeeld de hoek α in figuur 2 (zie hieronder). Linksom als de hoek positief is, en rechtsom als het een negatieve hoek is.
De straal met oorsprong O en hoek α wordt getekend, die de eenheidscirkel op punt P onderschept.Punt P wordt orthogonaal geprojecteerd op de horizontale as X, wat leidt tot punt C. Evenzo wordt P loodrecht op de verticale as Y geprojecteerd, waardoor plaats wordt gegeven aan het punt S.
We hebben de rechthoekige driehoek OCP bij C.
Sinus en cosinus
Er moet aan worden herinnerd dat de trigonometrische verhouding borst wordt als volgt gedefinieerd op een rechthoekige driehoek:
De sinus van een hoek van de driehoek is de verhouding of quotiënt tussen het been tegenover de hoek en de hypotenusa van de driehoek.
Toegepast op de driehoek OCP van figuur 2 zou het er als volgt uitzien:
Sen (α) = CP / OP
maar CP = OS en OP = 1, zodat:
Sen (α) = OS
Dit betekent dat het projectie-OS op de Y-as een waarde heeft die gelijk is aan de sinus van de weergegeven hoek. Opgemerkt moet worden dat de maximale waarde van de sinus van een hoek (+1) optreedt wanneer α = 90º en de minimumwaarde (-1) wanneer α = -90º of α = 270º.
Evenzo is de cosinus van een hoek het quotiënt tussen het been dat grenst aan de hoek en de hypotenusa van de driehoek..
Toegepast op de driehoek OCP van figuur 2 zou het er als volgt uitzien:
Cos (α) = OC / OP
maar OP = 1, zodat:
Cos (α) = OC
Dit betekent dat de projectie OC op de X-as een waarde heeft die gelijk is aan de sinus van de weergegeven hoek. Opgemerkt moet worden dat de maximale waarde van de cosinus (+1) optreedt wanneer α = 0º of α = 360º, terwijl de minimale waarde van de cosinus (-1) is wanneer α = 180º.
De fundamentele identiteit
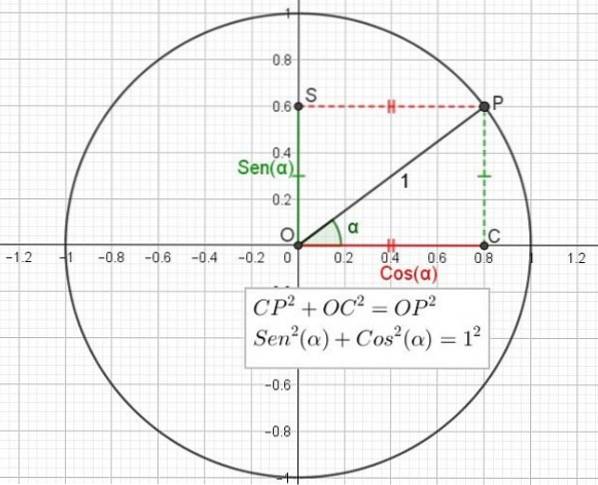
Voor de rechthoekige driehoek OCP in C wordt de stelling van Pythagoras toegepast, die stelt dat de som van het kwadraat van de benen gelijk is aan het kwadraat van de hypotenusa:
CPtwee + OCtwee = OPtwee
Maar er is al gezegd dat CP = OS = Sen (α), dat OC = Cos (α) en dat OP = 1, dus de vorige uitdrukking kan worden herschreven als een functie van de sinus en cosinus van de hoek:
Sentwee(α) + Costwee(α) = 1
De as van de raaklijn
Net zoals de X-as in de trigonometrische cirkel de cosinusas is en de Y-as de sinusas, is er op dezelfde manier de raaklijn (zie figuur 3) die precies de raaklijn is aan de eenheidscirkel op het punt B van coördinaten (1, 0).
Als je de waarde van de raaklijn van een hoek wilt weten, teken je de hoek van de positieve halve as van de X, het snijpunt van de hoek met de as van de raaklijn definieert een punt Q, de lengte van het segment OQ is de tangens van de hoek.
Dit komt doordat per definitie de tangens van hoek α het tegenoverliggende been QB is tussen het aangrenzende been OB. Dat wil zeggen, Tan (α) = QB / OB = QB / 1 = QB.
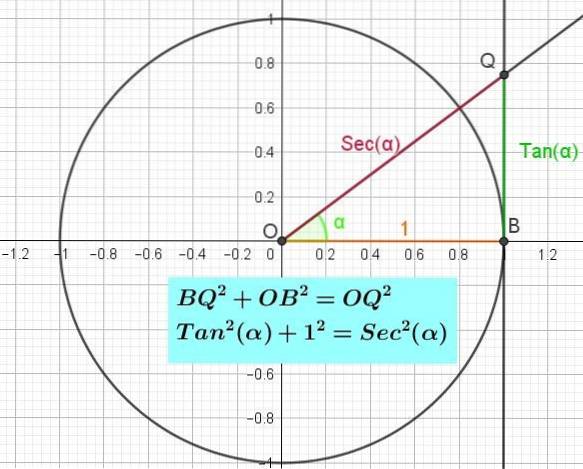
De Pythagorische identiteit van de raaklijn
De Pythagorische identiteit van de raaklijn kan worden bewezen door de rechthoekige driehoek OBQ bij B te beschouwen (Figuur 3). Als we de stelling van Pythagoras op deze driehoek toepassen, hebben we die BQtwee + OBtwee = OQtwee. Maar er is al gezegd dat BQ = Tan (α), dat OB = 1 en dat OQ = Sec (α), dus als we in de Pythagorische gelijkheid de rechthoekige driehoek OBQ vervangen, hebben we:
Zotwee(α) + 1 = Sectwee(α).
Voorbeeld
Controleer of de Pythagoras-identiteiten al dan niet vervuld zijn in de rechthoekige driehoek met benen AB = 4 en BC = 3.
Oplossing: de benen zijn bekend, de hypotenusa moet worden bepaald, namelijk:
AC = √ (AB ^ 2 + BC ^ 2) = √ (4 ^ 2 + 3 ^ 2) = √ (16 + 9) = √ (25) = 5.
De hoek ∡BAC wordt α, ∡BAC = α genoemd. Nu worden de trigonometrische verhoudingen bepaald:
Sen α = BC / AC = 3/5
Cos α = AB / AC = 4/5
Dus α = BC / AB = 3/4
Cotan α = AB / BC = 4/3
Sec α = AC / AB = 5/4
Csc α = AC / BC = 5/3
Het begint met de fundamentele trigonometrische identiteit:
Sentwee(α) + Costwee(α) = 1
(3/5) ^ 2 + (4/5) ^ 2 = 9/25 + 16/25 = (9 +16) / 25 = 25/25 = 1
Er wordt geconcludeerd dat het is vervuld.
- De volgende identiteit van Pythagoras is die van de raaklijn:
Zotwee(α) + 1 = Sectwee(α)
(3/4) ^ 2 + 1 = 9/16 + 16/16 = (9 + 16) / 16 = 25/16 = (5/4) ^ 2
En er wordt geconcludeerd dat de identiteit van de raaklijn wordt geverifieerd.
- Op een vergelijkbare manier die van de cotangens:
1 + Ctgtwee(α) = Csctwee(α)
1+ (4/3) ^ 2 = 1 + 16/9 = 25/9 = (5/3) ^ 2
Er wordt geconcludeerd dat het ook is vervuld, waarmee de taak van het verifiëren van de Pythagorische identiteiten voor de gegeven driehoek is voltooid.
Opgeloste oefeningen
Bewijs de volgende identiteiten, gebaseerd op de definities van de trigonometrische verhoudingen en de Pythagorische identiteiten.
Oefening 1
Bewijs dat Costwee x = (1 + Sen x) (1 - Sen x).
Oplossing: Aan de rechterkant wordt het opmerkelijke product van de vermenigvuldiging van een binominaal met zijn conjugaat herkend, wat, zoals bekend, een verschil in kwadraten is:
Costwee x = 1twee - Sentwee X
Dan gaat de term met sinus aan de rechterkant naar de linkerkant met het teken veranderd:
Costwee x + Sentwee x = 1
Merk op dat de fundamentele trigonometrische identiteit is bereikt, dus wordt geconcludeerd dat de gegeven uitdrukking een identiteit is, dat wil zeggen dat het waar is voor elke waarde van x.
Oefening 2
Uitgaande van de fundamentele trigonometrische identiteit en gebruikmakend van de definities van de trigonometrische verhoudingen, demonstreert u de Pythagorische identiteit van de cosecans.
Oplossing: de fundamentele identiteit is:
Sentwee(x) + Costwee(x) = 1
Beide leden zijn verdeeld over Sentwee(x) en de noemer wordt verdeeld in het eerste lid:
Sentwee(x) / Sentwee(x) + Costwee(x) / Sentwee(x) = 1 / Sentwee(X)
Het is vereenvoudigd:
1 + (Cos (x) / Sen (x)) ^ 2 = (1 / Sen (x)) ^ 2
Cos (x) / Sen (x) = Cotan (x) is een (niet-Pythagorische) identiteit die wordt geverifieerd door de definitie van de trigonometrische verhoudingen. Hetzelfde gebeurt met de volgende identiteit: 1 / Sen (x) = Csc (x).
Ten slotte moet je:
1 + Ctgtwee(x) = Csctwee(X)
Referenties
- Baldor J. (1973). Vlak- en ruimtegeometrie met een inleiding tot trigonometrie. Centraal-Amerikaanse culturele. AC.
- C. E. A. (2003). Geometrie-elementen: met oefeningen en geometrie van het kompas. Universiteit van Medellin.
- Campos, F., Cerecedo, F. J. (2014). Wiskunde 2. Grupo Redactie Patria.
- IGER. (s.f.). Wiskunde eerste semester Tacaná. IGER.
- Jr. geometrie. (2014). Veelhoeken. Lulu Press, Inc.
- Miller, Heeren en Hornsby. (2006). Wiskunde: redeneren en toepassingen (tiende editie). Pearson Education.
- Patiño, M. (2006). Wiskunde 5. Redactioneel Progreso.
- Wikipedia. Goniometrische identiteiten en formules. Hersteld van: es.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.