
Top 9 kenmerken van de rechthoek
De rechthoek het wordt gekenmerkt doordat het een platte geometrische figuur is met vier zijden en vier hoekpunten. Van deze vier zijden heeft één paar dezelfde maat, terwijl het andere paar een andere maat heeft dan die van het eerste paar..
Deze figuur is een veelhoek van het parallellogramtype, aangezien de tegenoverliggende zijden van een rechthoek evenwijdig zijn en dezelfde afmetingen hebben. De hoeken waaruit de rechthoeken bestaan, hebben een amplitude van 90 °, dus het zijn rechte hoeken. Dat is waar de naam vandaan komt rechthoek.

Het feit dat de rechthoeken vier hoeken met dezelfde amplitude hebben, zorgt ervoor dat deze geometrische figuren equiangles worden genoemd.
Wanneer een rechthoek wordt gekruist door een diagonale lijn, ontstaan er twee driehoeken. Als je een rechthoek met twee diagonale lijnen kruist, kruisen ze elkaar in het midden van de figuur.
9 hoofdkenmerken over rechthoeken
1- Aantal zijden en afmeting
Rechthoeken bestaan uit vier zijden. We kunnen deze zijden in twee paren verdelen: het ene paar zijden meet hetzelfde, terwijl het andere paar metingen hoger of lager heeft dan het vorige paar..
Tegengestelde zijden hebben dezelfde afmetingen, terwijl opeenvolgende zijden verschillende afmetingen hebben.
Daarbij zijn de rechthoeken tweedimensionale figuren, wat betekent dat ze maar twee afmetingen hebben: breedte en hoogte..
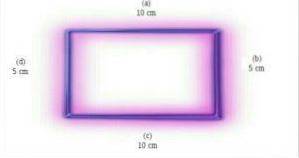
Het basiskenmerk van rechthoeken is dat ze vier zijden hebben. Dit zijn tweedimensionale figuren, omdat ze plat zijn. Foto opgehaald van en.wikipedia.org
2- Veelhoek
De rechthoeken zijn een veelhoek. In die zin zijn rechthoeken geometrische figuren, die worden begrensd door een gesloten veelhoekige lijn (dat wil zeggen, door een recht lijnsegment dat zichzelf sluit).
Om precies te zijn, rechthoeken zijn vierhoekige polygonen, omdat ze vier zijden hebben.
3- Het zijn geen gelijkzijdige polygonen
Een veelhoek is gelijkzijdig als al zijn zijden hetzelfde meten. De zijkanten van een rechthoek hebben niet dezelfde afmetingen. Om deze reden kan niet worden gezegd dat de rechthoeken gelijkzijdig zijn.
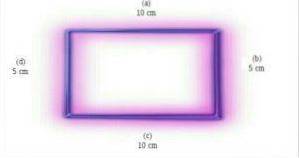
Rechthoeken zijn niet gelijkzijdig, omdat hun zijden verschillende maten hebben. In de bovenstaande afbeelding hebben zijden (a) en (c) dezelfde afmeting, die verschilt van de afmetingen van zijden (b) en (d). Foto opgehaald en aangepast van en.wikipedia.org
4- Gelijkhoekige veelhoek
Equiangular polygonen zijn die waarin ze bestaan uit hoeken met dezelfde amplitude.
Alle rechthoeken bestaan uit vier rechte hoeken (dat wil zeggen hoeken van 90 °). Een rechthoek van 10 cm x 20 cm heeft vier hoeken van 90 °, hetzelfde gebeurt met een rechthoek van grotere of kleinere afmeting.
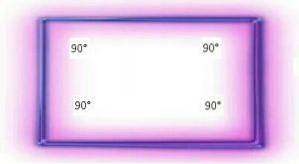
Alle rechthoeken zijn gelijke hoeken omdat hun hoeken dezelfde amplitude hebben. Dat wil zeggen 90 °. Foto opgehaald en aangepast van en.wikipedia.org
5- De oppervlakte van een rechthoek
De oppervlakte van een rechthoek is gelijk aan het product van de basis maal de hoogte, waarbij de basis de horizontale zijde is en de hoogte de verticale zijde. Een eenvoudigere manier om ernaar te kijken, is door de afmetingen van twee aangrenzende zijden te vermenigvuldigen.
De formule om de oppervlakte van deze geometrische figuur te berekenen is:
een = b X EEN
Enkele voorbeelden van het berekenen van de oppervlakte van een rechthoek zijn:
- Rechthoek met een basis van 5 cm en een hoogte van 2 cm. 5 cm x 2 cm = 10 cmtwee
- Rechthoek met een basis van 2 m en een hoogte van 0,5 m. 2m x 0,5m = 2mtwee
- Rechthoek met een basis van 18 m en een hoogte van 15 m. 18 mx 15 m = 270 mtwee
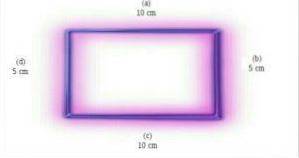
De rechthoek op de afbeelding heeft een basis van 10 cm en een hoogte van 5 cm. Het gebied is het product van 10 cm x 5 cm. In dit geval is de oppervlakte van de rechthoek 50 cmtwee. Foto opgehaald en aangepast van en.wikipedia.org
6- Rechthoeken zijn parallellogrammen
Vierhoeken kunnen in drie typen worden ingedeeld: trapezoïden, trapezoïden en parallellogrammen. Deze laatste worden gekenmerkt door twee paar evenwijdige zijden, die niet noodzakelijk dezelfde afmetingen hoeven te hebben..
In die zin zijn de rechthoeken parallellogrammen, aangezien twee paar zijden naar elkaar toe wijzen.
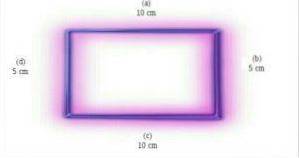
Rechthoeken zijn parallellogrammen omdat ze twee paar zijden hebben die evenwijdig zijn.. Zijden (a) en (c) zijn parallel. Zijden (b) en (d) zijn parallel. Foto opgehaald en aangepast van en.wikipedia.org
7- De tegenovergestelde hoeken zijn congruent en de opeenvolgende zijn complementair
De tegenovergestelde hoeken zijn die in de niet-opeenvolgende hoekpunten van de figuur. Terwijl opeenvolgende hoeken aangrenzende hoeken zijn, naast elkaar.
Twee hoeken zijn congruent als ze dezelfde amplitude hebben. Van hun kant zijn twee hoeken complementair wanneer de som van hun amplitudes een hoek van 180 ° oplevert, of wat hetzelfde is, een rechte hoek.
Alle hoeken van een rechthoek zijn 90 °, dus kan worden gezegd dat de tegenovergestelde hoeken van deze geometrische figuur congruent zijn.
Met betrekking tot opeenvolgende hoeken is de rechthoek opgebouwd uit hoeken van 90 °. Als de opeenvolgende worden toegevoegd, is het resultaat 180 °. Het gaat dus over complementaire invalshoeken.
8- Het wordt gevormd door twee rechthoekige driehoeken
Als een diagonaal wordt getekend in de rechthoek (een lijn die van de ene hoek van de rechthoek naar de andere gaat die er tegenover staat), worden twee rechthoekige driehoeken verkregen. Dit type driehoek is er een die wordt gevormd door een rechte hoek en twee scherpe hoeken.

In de afbeelding vertegenwoordigt de steeklijn de diagonaal. Dit verdeelt de rechthoek in twee driehoeken. Foto opgehaald en aangepast van en.wikipedia.org
9- De diagonalen snijden elkaar in het midden
Zoals al uitgelegd, zijn de diagonalen de lijnen die van een van de hoeken naar een andere tegenovergestelde hoek gaan. Als er twee diagonalen in de rechthoek worden getekend, snijden ze elkaar in het midden van de figuur.
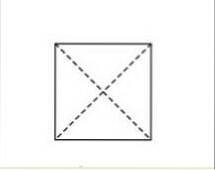
De stippellijnen stellen de diagonalen voor. Deze lijnen snijden elkaar precies in het midden van de rechthoek. Foto opgehaald en aangepast van dummies.com
Referenties
- Rechthoek. Opgehaald op 24 juli 2017, van mathisfun.com.
- Rechthoek. Opgehaald op 24 juli 2017, via merriam-webster.com.
- Eigenschappen van ruiten, rechthoeken en vierkanten. Opgehaald op 24 juli 2017, via dummies.com.
- Rechthoek. Opgehaald op 24 juli 2017, via en.wikipedia.org.
- Rechthoek. Opgehaald op 24 juli 2017, via collinsdictionary.com.
- Geometrische basisvormen. Opgehaald op 24 juli 2017, via universalclass.com.
- Vierhoeken. Opgehaald op 24 juli 2017, van mathisfun.coma.

Niemand heeft nog op dit artikel gereageerd.