De De wet van Faraday in elektromagnetisme stelt dat een veranderende magnetische veldflux in staat is om een elektrische stroom in een gesloten circuit op te wekken.
In 1831 experimenteerde de Engelse natuurkundige Michael Faraday met bewegende geleiders binnen een magnetisch veld en ook met variërende magnetische velden die door vaste geleiders gingen..
Faraday realiseerde zich dat als hij de magnetische veldflux in de loop van de tijd varieerde, hij in staat was een spanning vast te stellen die evenredig is met die variatie. Als ε de spanning of geïnduceerde elektromotorische kracht is (geïnduceerde emf) en Φ de magnetische veldflux is, kan dit in wiskundige vorm worden uitgedrukt:
| ε | = ΔΦ / Δt
Waar het symbool Δ de variatie van de hoeveelheid aangeeft en de balken in de emf de absolute waarde hiervan aangeven. Omdat het een gesloten circuit is, kan de stroom in de ene of de andere richting stromen.
Magnetische flux, geproduceerd door een magnetisch veld over een oppervlak, kan op een aantal manieren variëren, bijvoorbeeld:
-Een staafmagneet door een cirkelvormige lus bewegen.
-Verhogen of verlagen van de intensiteit van het magnetische veld dat door de lus gaat.
-Het veld laten staan, maar door middel van een of ander mechanisme het gebied van de lus veranderen.
-Combinatie van de bovenstaande methoden.
Artikel index
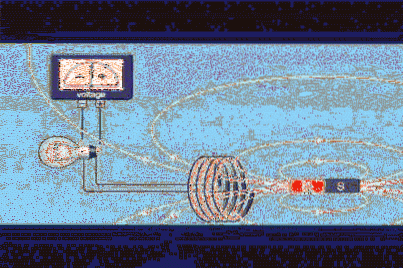
Stel dat je een gesloten circuit hebt van gebied A, zoals een cirkelvormige lus of wikkeling gelijk aan die in figuur 1, en dat je een magneet hebt die een magnetisch veld produceert B.
De magnetische veldflux Φ is een scalaire grootheid die verwijst naar het aantal veldlijnen dat gebied A doorkruist.In figuur 1 zijn de witte lijnen die de noordpool van de magneet verlaten en terugkeren door het zuiden..
De intensiteit van het veld zal evenredig zijn met het aantal lijnen per oppervlakte-eenheid, dus we kunnen zien dat het aan de polen erg intens is. Maar we kunnen een zeer intens veld hebben dat geen flux in de lus produceert, wat we kunnen bereiken door de oriëntatie hiervan (of de magneet) te veranderen.
Om rekening te houden met de oriëntatiefactor, wordt de magnetische veldflux gedefinieerd als het scalaire product daartussen B Y n, wezen n de eenheidsnormaalvector naar het oppervlak van de lus en dat geeft de oriëntatie aan:
Φ = Bn A = BA.cosθ
Waar θ de hoek tussen is B Y n. Als bijvoorbeeld B Y n loodrecht staan, is de magnetische veldflux nul, omdat in dat geval het veld raakt aan het vlak van de lus en niet door het oppervlak kan gaan.
In plaats daarvan ja B Y n parallel zijn, betekent dit dat het veld loodrecht op het vlak van de lus staat en de lijnen er zo ver mogelijk doorheen gaan.
De eenheid in het internationale systeem voor F is de weber (W), waarbij 1 W = 1 T.mtwee (lees 'tesla per vierkante meter').
In figuur 1 kunnen we zien dat de polariteit van de spanning verandert als de magneet beweegt. De polariteit wordt bepaald door de wet van Lenz, die stelt dat de geïnduceerde spanning de variatie moet tegengaan die deze produceert.
Als bijvoorbeeld de door de magneet geproduceerde magnetische flux toeneemt, ontstaat er een stroom in de geleider die circuleert en zijn eigen flux creëert, die deze toename tegenwerkt..
Als daarentegen de door de magneet opgewekte flux afneemt, circuleert de geïnduceerde stroom zodanig dat zijn eigen flux deze afname tegengaat..
Om met dit fenomeen rekening te houden, wordt een minteken voor de wet van Faraday geplaatst en is het niet langer nodig om de balken met absolute waarde te plaatsen:
ε = -ΔΦ / Δt
Dit is de wet van Faraday-Lenz. Als de stroomvariatie oneindig klein is, worden de delta's vervangen door verschillen:
ε = -dΦ / dt
De bovenstaande vergelijking is geldig voor een lus. Maar als we een spoel van N-beurten hebben, is het resultaat veel beter, omdat de emf N keer wordt vermenigvuldigd:
ε = - N (dΦ / dt)
Om de stroom in te schakelen, moet er een relatieve beweging zijn tussen de magneet en de lus. Dit is een van de manieren waarop de flux kan variëren, omdat op deze manier de intensiteit van het veld dat door de lus gaat, verandert..
Zodra de beweging van de magneet stopt, gaat de lamp uit, ook als de magneet nog in het midden van de lus staat. Wat nodig is om de stroom te laten circuleren die de lamp inschakelt, is dat de veldflux varieert.
Wanneer het magnetische veld in de tijd varieert, kunnen we dit uitdrukken als:
B B (t).
Door het gebied A van de lus constant te houden en het vast te laten in een constante hoek, die in het geval van de figuur 0º is, dan:
Als het mogelijk is om het gebied van de lus te veranderen, de oriëntatie vast te laten en deze in het midden van een constant veld te plaatsen, wordt de geïnduceerde emf gegeven door:
Een manier om dit te bereiken, is door een staaf te plaatsen die met een bepaalde snelheid op een stroomrail schuift, zoals weergegeven in de volgende afbeelding.
De staaf en de rail, plus een gloeilamp of een weerstand verbonden met geleidende draden, vormen een gesloten circuit in de vorm van een rechthoekige lus..
Bij het verschuiven van de balk is de lengte X neemt toe of af, en daarmee verandert het gebied van de lus, wat voldoende is om een variabele stroom te creëren.
Zoals we al eerder zeiden, als de hoek tussen B en de normaal van de lus is gemaakt om te variëren, de veldflux verandert volgens:
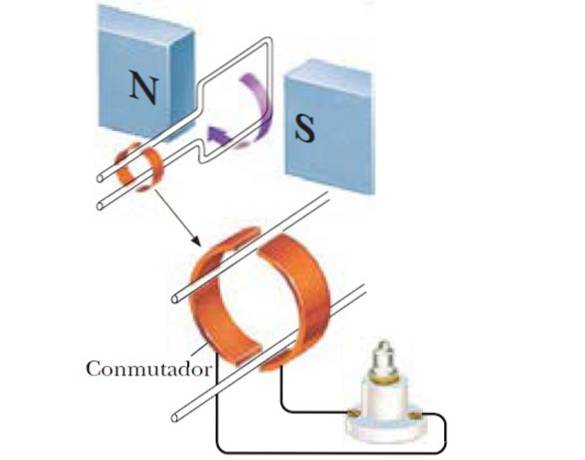
Aldus wordt een sinusvormige generator verkregen en als in plaats van een enkele spoel een aantal N spoelen wordt gebruikt, is de geïnduceerde emf groter:
Een cirkelvormige spoel van N draait en straal R, roteert met hoekfrequentie ω in het midden van een magnetisch veld van magnitude B. Zoek een uitdrukking voor de maximale emf geïnduceerd in de spoel.
De uitdrukking voor de emf geïnduceerd door rotatie wordt toegepast wanneer de spoel N-windingen heeft, wetende dat:
-Het gebied van de spoel is A = πRtwee
-De hoek θ varieert als functie van de tijd als θ = ωt
Het is belangrijk op te merken dat de eerste θ = ωt wordt vervangen door de wet van Faraday en spoedig is afgeleid met betrekking tot de tijd:
ε = -NBA (cos θ) '= -NB (πRtwee). [cos (ωt)] '= NBω (πRtwee) zonde (ωt)
Omdat de maximale emf wordt gevraagd, treedt deze op wanneer sin ωt = 1, dus tenslotte:
εmax. hoogte = NBω (πRtwee
Niemand heeft nog op dit artikel gereageerd.