Maatregelen van positie, centrale neiging en spreiding

De maatregelen van centrale neiging, spreiding en positie, zijn waarden die worden gebruikt om een ​​set statistische gegevens correct te interpreteren. Deze kunnen direct worden bewerkt, aangezien ze zijn verkregen uit de statistische studie, of ze kunnen worden georganiseerd in groepen van gelijke frequentie, wat de analyse vergemakkelijkt..

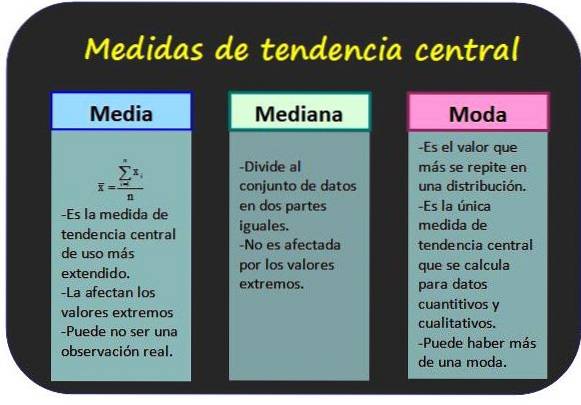
Maatregelen van centrale tendens

Ze maken het mogelijk om te weten rond welke waarden de statistische gegevens zijn gegroepeerd.

Rekenkundig gemiddelde

Het staat ook bekend als het gemiddelde van de waarden van een variabele en wordt verkregen door alle waarden op te tellen en het resultaat te delen door het totale aantal gegevens.

• Rekenkundig gemiddelde voor niet-gegroepeerde gegevens

Laat een variabele x zijn waarvan we n gegevens hebben zonder te organiseren of te groeperen, het rekenkundig gemiddelde wordt als volgt berekend:

En in sommatie-notatie:

Voorbeeld

De eigenaren van een toeristenherberg in de bergen zijn van plan te weten hoeveel dagen de bezoekers gemiddeld in de faciliteiten verblijven. Hiervoor werd een registratie bijgehouden van de permanentie-dagen van 20 groepen toeristen, waarbij de volgende gegevens werden verkregen:

1; 1; twee; twee; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; twee; twee; 3; 4; 1

Het gemiddeld aantal dagen dat toeristen verblijven is:

• Rekenkundig gemiddelde voor gegroepeerde gegevens

Als de gegevens van de variabele zijn georganiseerd in een tabel met absolute frequenties f_ik en de klassencentra zijn x₁, X_twee,..., x_n, het gemiddelde wordt berekend door:

In sommatie-notatie:

Mediaan

De mediaan van een groep van n waarden van de variabele x is de centrale waarde van de groep, mits de waarden in oplopende volgorde zijn gerangschikt. Op deze manier is de helft van alle waarden kleiner dan de modus en de andere helft groter..

• Mediaan van niet-gegroepeerde gegevens

De volgende gevallen kunnen voorkomen:

-Aantal n waarden van de variabele x  vreemd: de mediaan is de waarde die precies in het midden van de waardengroep ligt:

-Aantal n waarden van de variabele x paar-: in dit geval wordt de mediaan berekend als het gemiddelde van de twee centrale waarden van de gegevensgroep:

Voorbeeld

Om de mediaan van de gegevens van het toeristenhostel te vinden, worden ze eerst gerangschikt van laag naar hoog:

1; 1; 1; 1; 1; 1; 1; twee; twee; twee​ twee​3; 3; 3; 4; 4; 4; 4; 5; 5

Het aantal gegevens is even, daarom zijn er twee centrale gegevens: X₁₀ en X_elf en aangezien beide 2 waard zijn, is hun gemiddelde ook.

Mediaan = 2

• Mediaan van gepoolde gegevens

De volgende formule wordt gebruikt:

De symbolen in de formule betekenen:

-c: breedte van het interval dat de mediaan bevat

-B._M.: ondergrens van hetzelfde interval

-F._m: aantal waarnemingen in het interval waartoe de mediaan behoort.

-n: totale gegevens.

-F._BM: aantal waarnemingen voordat van het interval dat de mediaan bevat.

mode

De modus voor niet-gegroepeerde gegevens is de waarde met de hoogste frequentie, terwijl dit voor gegroepeerde gegevens de klasse met de hoogste frequentie is. Mode wordt beschouwd als de meest representatieve gegevens of klasse van de distributie.

Twee belangrijke kenmerken van deze maatregel zijn dat een dataset meer dan één modus kan hebben, en de modus kan worden bepaald voor zowel kwantitatieve als kwalitatieve gegevens..

Voorbeeld

Verdergaand met de gegevens van de toeristische parador, degene die het meest wordt herhaald is 1, daarom is het meest gebruikelijke dat toeristen 1 dag in de parador blijven.

Maatregelen van verspreiding

Verspreidingsmetingen beschrijven hoe geclusterd de gegevens zijn rond de centrale metingen.

Rang

Het wordt berekend door de grootste gegevens en de kleinste gegevens af te trekken. Als dit verschil groot is, is dit een teken dat de gegevens verspreid zijn, terwijl kleine waarden aangeven dat de gegevens dicht bij het gemiddelde liggen..

Voorbeeld

Het bereik voor de gegevens van de toeristische parador is:

Bereik = 5−1 = 4

Variantie

• Variantie voor niet-gegroepeerde gegevens

Om de variantie s te vinden^twee Het is vereist om eerst het rekenkundig gemiddelde te kennen, daarna wordt het kwadraatverschil tussen elk gegeven en het gemiddelde berekend, ze worden allemaal opgeteld en gedeeld door het totale aantal waarnemingen. Deze verschillen staan ​​bekend als afwijkingen.

De variantie, die altijd positief (of nul) is, geeft aan hoe ver de waarnemingen van het gemiddelde zijn: als de variantie hoog is, zijn de waarden meer verspreid dan wanneer de variantie klein is.

Voorbeeld

De variantie voor de gegevens van het toeristenhostel is:

1; 1; twee; twee; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; twee; twee; 3; 4; 1

• Variantie voor gegroepeerde gegevens

Om de variantie van een gegroepeerde dataset te vinden, is het volgende nodig: i) het gemiddelde, ii) de frequentie f_ik  dat zijn de totale gegevens in elke klasse en iii) x_ik  of klasse waarde:

De standaarddeviatie is de positieve vierkantswortel van de variantie, dus het heeft een voordeel ten opzichte van de variantie: het komt in dezelfde eenheden als de variabele die wordt bestudeerd en dus heb je een directer idee van hoe dichtbij of ver de variabele is van gemiddeld.

• Standaarddeviatie voor niet-gegroepeerde gegevens

Het wordt eenvoudig bepaald door de vierkantswortel van de variantie voor niet-gegroepeerde gegevens te vinden:

De standaarddeviatie voor de gegevens van het toeristenhostel is:

s = √ (s^twee) = √1,95 = 1,40

• Standaarddeviatie voor gegroepeerde gegevens

Het wordt berekend door de vierkantswortel van de variantie voor gegroepeerde gegevens te vinden:

Positiemetingen

Metingen van positie verdelen een geordende set gegevens in stukken van gelijke grootte. De mediaan is niet alleen een maat voor de centrale neiging, maar ook een maat voor de positie, aangezien deze het geheel in twee gelijke delen verdeelt. Maar kleinere delen kunnen worden verkregen met kwartielen, decielen en percentielen.

Kwartielen

De kwartielen verdelen de set in vier gelijke delen die elk 25% van de gegevens bevatten. Ze worden aangeduid als Q₁, Q_twee en Q₃ en de mediaan is het kwartiel Q_twee. Op deze manier bevindt 25% van de gegevens zich onder het Q-kwartiel.₁, 50% onder het Q-kwartiel_twee of mediaan en 75% onder het Q-kwartiel₃.

• Kwartielen voor niet-gegroepeerde gegevens

De gegevens zijn geordend en het totaal is verdeeld in 4 groepen met elk hetzelfde aantal gegevens. De positie van het eerste kwartiel wordt gevonden door:

Q₁ = (n + 1) / 4

Waarbij n de totale gegevens is. Als het resultaat een geheel getal is, worden de gegevens die overeenkomen met die positie gelokaliseerd, maar als het decimaal is, wordt het gemiddelde van de gegevens die overeenkomen met het gehele deel met de volgende, of voor een grotere precisie wordt het lineair geïnterpoleerd tussen de genoemde gegevens.

Voorbeeld

De positie van het eerste kwartiel Q₁ voor de gegevens van de toeristische parador is:

Q₁ = (n + 1) / 4 = (20 + 1) / 4 = 5,25

Dit is de positie van kwartiel 1 en aangezien het resultaat decimaal is, wordt de data X doorzocht₅ en X_6, die respectievelijk X zijn₅ = 1 en X₆ = 1 en worden gemiddeld, resulterend in:

Eerste kwartiel = 1

1; 1; 1; 1; 1​ 1​1; twee; twee​ twee; twee; 3; 3; 3; 4; 4; 4; 4; 5; 5.

De positie van het tweede kwartiel Q_twee het is:

Q_twee = 2 (n + 1) / 4 = 10,5

Wat is het gemiddelde tussen X₁₀ en X_elf en komt overeen met de mediaan:

Tweede kwartiel = Mediaan = 2

De positie van het derde kwartiel wordt berekend door:

Q₃ = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15,75

Het is ook decimaal, daarom wordt X gemiddeld_vijftien en X₁₆​

1; 1; 1; 1; 1; 1; 1; twee; twee​ twee; twee; 3; 3; 3; 4​ 4​4; 4; 5; 5.

Maar aangezien beide 4 waard zijn:

Derde kwartiel = 4

De algemene formule voor de positie van kwartielen in niet-gegroepeerde gegevens is:

Q_k = k (n + 1) / 4

Met k = 1,2,3.

• Kwartielen voor gegroepeerde gegevens

Ze worden op dezelfde manier berekend als de mediaan:

De uitleg van de symbolen is:

-B._Q: ondergrens van het interval met het kwartiel

-c: breedte van dat interval

-F._wat: aantal waarnemingen in het kwartielinterval.

-n: totale gegevens.

-F._BQ: aantal gegevens voordat van het interval dat het kwartiel bevat.

Decielen en percentielen

De decielen en percentielen verdelen de dataset in respectievelijk 10 gelijke delen en 100 gelijke delen, en hun berekening wordt op dezelfde manier uitgevoerd als die van de kwartielen..

• Decielen en percentielen voor niet-gegroepeerde gegevens

De formules worden respectievelijk gebruikt:

D_k = k (n + 1) / 10

Met k = 1,2,3… 9.

Decile D₅ moet gelijk zijn aan de mediaan.

P._k = k (n + 1) / 100

Met k = 1,2,3… 99.

Het P-percentiel_vijftig moet gelijk zijn aan de mediaan.

Voorbeeld

In het voorbeeld van het toeristenherberg is de positie van de D₃ het is:

D₃ = 3 (20 + 1) / 10 = 6,3

Omdat het een decimaal getal is, wordt X gemiddeld₆ en X_7, beide gelijk aan 1:

1; 1; 1; 1; 1; 1​ 1​twee; twee; twee; twee; 3; 3; 3; 4; 4; 4; 4; 5; 5

Dit betekent dat 3 tiende van de gegevens onder X ligt₇ = 1 en de overige hierboven.

• Decielen en percentielen voor gegroepeerde gegevens

De formules zijn analoog aan die voor kwartielen. D wordt gebruikt om decielen aan te duiden en P voor percentielen, en de symbolen worden op dezelfde manier geïnterpreteerd:

De empirische regel

Wanneer de gegevens symmetrisch zijn verdeeld en de distributie unimodaal is, wordt er een regel aangeroepen  empirische regel of regel 68 - 95 - 99, die ze groepeert in de volgende intervallen:

• 68% van de gegevens valt binnen het bereik:

• 95% van de gegevens valt binnen het bereik:

• 99% van de gegevens valt binnen het bereik:

Voorbeeld

In welke interval is 95% van de gegevens van de toeristenparador?

Ze bevinden zich in het interval: [2.5−1.40; 2,5 + 1,40] = [1,1; 3.9].

Referenties

1. Berenson, M. 1985. Statistieken voor management en economie. Interamericana S.A.
2. Devore, J. 2012. Waarschijnlijkheid en statistiek voor techniek en wetenschap. 8e. Editie. Cengage.
3. Levin, R. 1988. Statistieken voor beheerders. 2e. Editie. Prentice hal.
4. Spiegel, M. 2009. Statistieken. Schaum-serie. 4e Editie. Mcgraw heuvel.
5. Walpole, R. 2007. Waarschijnlijkheid en statistiek voor techniek en wetenschappen. Pearson.