
Aanvullende invalshoeken wat zijn het, berekeningen, voorbeelden, oefeningen
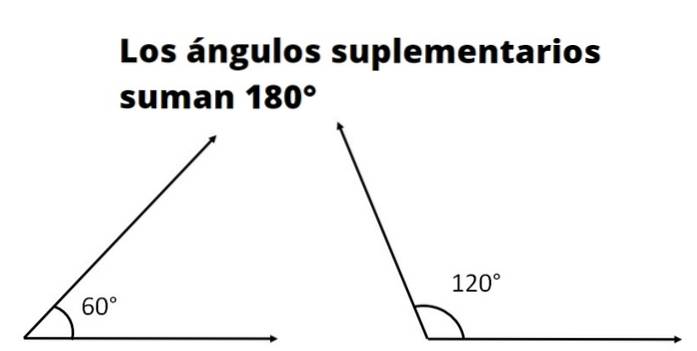
Twee of meer zijn aanvullende hoeken als de som van zijn maten overeenkomt met de maat van een rechte hoek. De maat van een rechte hoek, ook wel een vlakke hoek genoemd, is in graden 180º en in radialen π.
We vinden bijvoorbeeld dat de drie binnenhoeken van een driehoek aanvullend zijn, aangezien de som van hun maten 180 ° is. Drie hoeken worden getoond in figuur 1. Uit het bovenstaande volgt dat α en β aanvullend zijn, aangezien ze aangrenzend zijn en hun som een rechte hoek vormt.
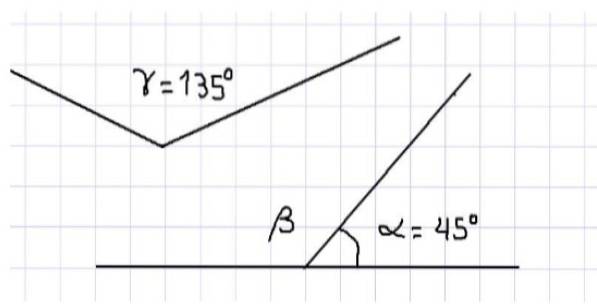
Ook in dezelfde figuur hebben we de hoeken α en γ die ook aanvullend zijn, omdat de som van hun maten gelijk is aan de maat van een vlakke hoek, dat wil zeggen 180º. Er kan niet gezegd worden dat de hoeken β en γ aanvullend zijn omdat, aangezien beide hoeken stomp zijn, hun afmetingen groter zijn dan 90º en daarom hun som groter is dan 180º..
Aan de andere kant kan worden gesteld dat de maat van hoek β gelijk is aan de maat van hoek γ, aangezien als β aanvullend is op α en γ aanvullend is op α, dan β = γ = 135º.
Artikel index
- 1 Voorbeelden
- 1.1 Voorbeeld A
- 1.2 Voorbeeld B
- 1.3 Voorbeeld C
- 1.4 Voorbeeld D
- 1.5 Voorbeeld E
- 1.6 Voorbeeld F
- 2 oefeningen
- 2.1 - Oefening I
- 2.2 - Oefening II
- 2.3 - Oefening III
- 3 aanvullende hoeken in twee parallellen gesneden door een secans
- 3.1 - Oefening IV
- 4 referenties
Voorbeelden
In de volgende voorbeelden wordt gevraagd om de onbekende hoeken te vinden, aangegeven met vraagtekens in figuur 2. Ze variëren van de eenvoudigste voorbeelden tot wat uitgebreider, zodat de lezer voorzichtiger moet zijn.
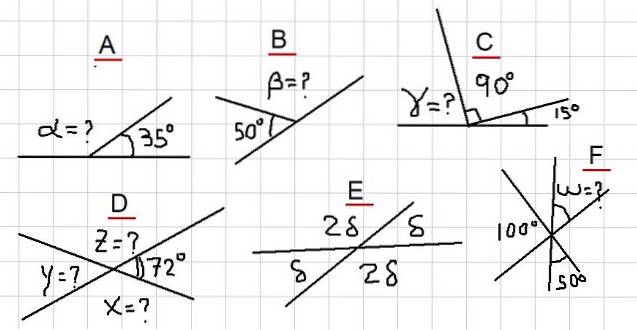
Voorbeeld A
In de figuur hebben we dat de aangrenzende hoeken α en 35º optellen tot een vlakke hoek. Dat wil zeggen, α + 35º = 180º en daarom is het waar dat: α = 180º- 35º = 145º.
Voorbeeld B
Aangezien β aanvullend is met de hoek van 50º, volgt β = 180º - 50º = 130º.
Voorbeeld C
Uit figuur 2C blijkt de volgende som: γ + 90º + 15º = 180º. Dat wil zeggen, γ is aanvullend met de hoek 105º = 90º + 15º. Er wordt dan geconcludeerd dat:
γ = 180º - 105º = 75º
Voorbeeld D
Aangezien X aanvullend is op 72º, volgt hieruit dat X = 180º - 72º = 108º. Verder is Y aanvullend bij X, dus Y = 180º - 108º = 72º.
En tenslotte is Z aanvullend met 72º, dus Z = 180º - 72º = 108º.
Voorbeeld E
De hoeken δ en 2δ zijn aanvullend, dus δ + 2δ = 180º. Wat betekent dat 3δ = 180º, en dit stelt ons op zijn beurt in staat om te schrijven: δ = 180º / 3 = 60º.
Voorbeeld F
Als we de hoek tussen 100º en 50º U noemen, dan is U een aanvulling daarop, omdat wordt opgemerkt dat hun som een vlakke hoek voltooit.
Hieruit volgt onmiddellijk dat U = 150º. Omdat U tegenover het hoekpunt van W staat, is W = U = 150º.
Opleiding
Hieronder worden drie oefeningen voorgesteld, waarbij in alle gevallen de waarde van de hoeken A en B in graden moet worden gevonden, zodat voldaan wordt aan de relaties getoond in figuur 3. Het concept van aanvullende hoeken wordt gebruikt om ze allemaal op te lossen..
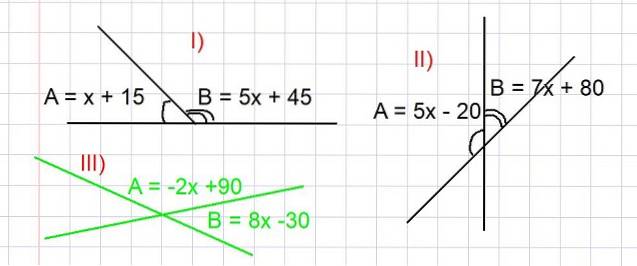
- Oefening I
Bepaal de waarden van hoeken A en B uit deel I) van figuur 3.
Oplossing
A en B zijn aanvullend, waarvan we hebben dat A + B = 180 graden, dan wordt de uitdrukking van A en B vervangen als een functie van x, zoals weergegeven in de afbeelding:
(x + 15) + (5x + 45) = 180
Er wordt een lineaire vergelijking van de eerste orde verkregen. Om het op te lossen, worden de termen onmiddellijk gegroepeerd:
6 x + 60 = 180
Als we beide leden door 6 delen, hebben we:
x + 10 = 30
En tot slot het oplossen, volgt hieruit dat x 20 ° waard is.
Nu moeten we de waarde van x inpluggen om de gevraagde hoeken te vinden. De hoek A is dus: A = 20 +15 = 35º.
En van zijn kant is hoek B B = 5 * 20 + 45 = 145º.
- Oefening II
Zoek de waarden van hoeken A en B uit deel II) van figuur 3.
Oplossing
Omdat A en B aanvullende hoeken zijn, hebben we dat A + B = 180 graden. Als we de uitdrukking voor A en B substitueren als een functie van x gegeven in deel II) van figuur 3, hebben we:
(-2x + 90) + (8x - 30) = 180
Opnieuw wordt een eerste graadsvergelijking verkregen, waarvoor de termen handig moeten worden gegroepeerd:
6 x + 60 = 180
Als we beide leden door 6 delen, hebben we:
x + 10 = 30
Hieruit volgt dat x 20 ° waard is.
Met andere woorden, de hoek A = -2 * 20 + 90 = 50º. Terwijl hoek B = 8 * 20 - 30 = 130º.
- Oefening III
Bepaal de waarden van hoeken A en B uit deel III) van figuur 3 (in groene kleur).
Oplossing
Omdat A en B aanvullende hoeken zijn, hebben we dat A + B = 180 graden. We moeten de uitdrukking voor A en B vervangen als een functie van x gegeven in figuur 3, waaruit we hebben:
(5x - 20) + (7x + 80) = 180
12 x + 60 = 180
Als we beide leden door 12 delen om de waarde van x op te lossen, hebben we:
x + 5 = 15
Uiteindelijk blijkt dat x 10 graden waard is.
Nu gaan we verder met substitueren om de hoek A te vinden: A = 5 * 10 -20 = 30º. En voor hoek B: B = 7 * 10 + 80 = 150º
Aanvullende hoeken in twee parallellen gesneden door een secans
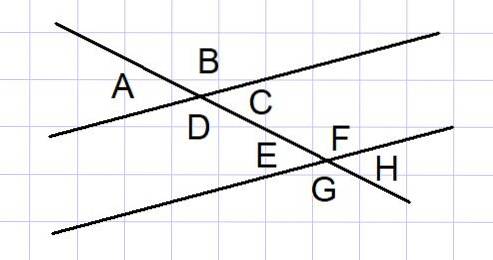
Twee parallelle lijnen die door een secans zijn gesneden, is bij sommige problemen een veel voorkomende geometrische constructie. Tussen dergelijke lijnen worden 8 hoeken gevormd zoals weergegeven in figuur 4.
Van die 8 hoeken zijn enkele paren hoeken aanvullend, die we hieronder opsommen:
- De buitenhoeken A en B, en de buitenhoeken G en H
- De binnenhoeken D en C, en de binnenhoeken E en F
- De buitenhoeken A en G, en de buitenhoeken B en H
- De binnenhoeken D en E, en de interieurs C en F
Voor de volledigheid worden de hoeken die aan elkaar gelijk zijn ook genoemd:
- De interne plaatsvervangers: D = F en C = E
- De externe plaatsvervangers: A = H en B = G
- De overeenkomstige: A = E en C = H
- Tegenstellingen door hoekpunt A = C en E = H
- De overeenkomstige: B = F en D = G
- Tegenstellingen door hoekpunt B = D en F = G
- Oefening IV
Verwijzend naar figuur 4, die de hoeken toont tussen twee parallelle lijnen gesneden door een secans, bepaal de waarde van alle hoeken in radialen, wetende dat de hoek A = π / 6 radialen.
Oplossing
A en B zijn aanvullende externe hoeken, dus B = π - A = π - π / 6 = 5π / 6
A = E = C = H = π / 6
B = F = D = G = 5π / 6
Referenties
- Baldor, J. A. 1973. Vliegtuig- en ruimtegeometrie. Centraal-Amerikaanse culturele.
- Wiskundige wetten en formules. Hoekmeetsystemen. Hersteld van: ingemecanica.com.
- Wentworth, G. Vliegtuiggeometrie. Hersteld van: gutenberg.org.
- Wikipedia. Aanvullende hoeken. Hersteld van: es.wikipedia.com
- Wikipedia. Transportband. Hersteld van: es.wikipedia.com
- Zapata F. Goniómetro: geschiedenis, onderdelen, bediening. Hersteld van: lifeder.com


Niemand heeft nog op dit artikel gereageerd.