De Froude nummer in hydraulica geeft het de relatie aan die bestaat tussen de traagheidskrachten en de zwaartekrachten voor een vloeistof. Daarom is het een manier om het volgende quotiënt aan te duiden:
WaarF. is de notatie voor het Froude-getal, een dimensieloze hoeveelheid die deze naam krijgt ter ere van de opmerkelijke Britse scheepsarchitect en waterbouwkundig ingenieur William Froude (1810-1879). Froude en zijn zoon experimenteerden door vlakke platen door het water te slepen om de weerstand van boten tegen golven in te schatten.
Bij de werking van de golven veroorzaakt door een boot tijdens het varen of de stroming op de pilaar van een brug, zijn de traagheidskrachten en de zwaartekracht aanwezig.
Het Froude-getal is vooral belangrijk bij het karakteriseren van vloeistofstroom in een open kanaal. Een open pijp of kanaal is een leiding waarvan het bovenoppervlak open is naar de atmosfeer. Voorbeelden zijn er in overvloed in de natuur, in de vorm van rivieren en beken.
En in door de mens gemaakte constructies hebben we:
-Goten en afvoeren in straten en gebouwen om regenwater af te voeren.
-Sloten voor irrigatie.
-Stortplaatsen en afvoeren.
-Koelkanalen voor industriële machines.
Dit zijn allemaal voorbeelden van pijpen die openstaan naar de atmosfeer, waarbij bij het karakteriseren van de stroming altijd rekening moet worden gehouden met het Froudegetal..
Artikel index
Het quotiënt dat aan het begin is aangegeven, tussen de traagheidskrachten en die van de zwaartekracht, heeft de volgende vorm, afhankelijk van de parameters van de vloeistof:
De vorige vergelijking of de vierkantswortel is het Froude-getal:
Zoals aan het begin uitgelegd, is de stroming van water door kanalen die naar de atmosfeer openen zeer frequent. Voor deze gevallen wordt de berekening van het Froude-getal uitgevoerd door de volgende formule toe te passen:
NF. = v / (gyh ½
Waar Yh is de hydraulische diepte, v is de gemiddelde stroomsnelheid en g is de waarde van de versnelling als gevolg van de zwaartekracht. De hydraulische diepte wordt op zijn beurt als volgt berekend:
Yh = A / T
In deze formule vertegenwoordigt A het netto oppervlak van de dwarsdoorsnede en is T de breedte van het vrije oppervlak van de vloeistof, degene die wordt blootgesteld aan de atmosfeer, aan de bovenkant van het kanaal of de buis. Het is geldig voor een rechthoekig kanaal of een kanaal dat breed genoeg is en met een constante diepte.
Het is belangrijk om te benadrukken dat, aangezien NF dimensieloos is, het product gyh het moet het kwadraat van een snelheid zijn. Er kan inderdaad worden aangetoond dat:
coftwee = gyh
Met cof als de voortplantingssnelheid van een oppervlaktegolf, analoog aan de geluidssnelheid in een vloeistof. Daarom is het Froude-getal ook analoog aan het Mach-getal, dat veel wordt gebruikt om de snelheid van vliegtuigen te vergelijken met die van geluid..
De vloeistofstroom in een open kanaal wordt ingedeeld in drie regimes, volgens de waarde van NF.
-Wanneer nF. < 1, se tiene un movimiento en régimen lento o onderkritisch.
-ZonderF. = 1 de stroom krijgt een naam kritische stroom.
-Eindelijk als je N hebtF. > 1 de beweging wordt uitgevoerd in snelle of superkritisch.
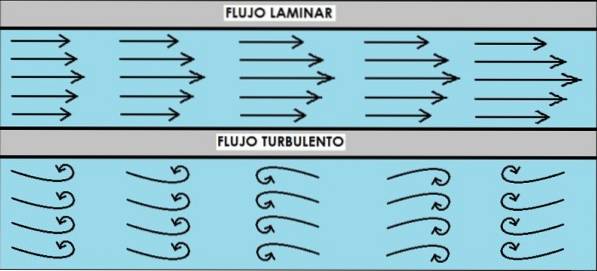
Reynolds nummer NR is een andere dimensieloze grootheid die erg belangrijk is bij de analyse van de vloeistofstroom, waardoor bekend is wanneer de vloeistof zich gedraagt laminaat en wanneer is het turbulent. Deze concepten zijn toepasbaar op zowel gesloten buis- als open kanaalstromen..
Een stroming is laminair wanneer de vloeistof soepel en ordelijk beweegt in lagen die niet mengen. Aan de andere kant wordt de turbulente stroming gekenmerkt door chaotisch en wanordelijk.
Een manier om erachter te komen of een waterstroom laminair of turbulent is, is door een stroom inkt te injecteren. Als de stroom laminair is, stroomt de inktstroom apart van die van water, maar als het een turbulente stroom is, mengt de inkt zich en verdwijnt deze snel in het water.
In die zin hebben we bij het combineren van de effecten van het Froude-getal met die van het Reynolds-getal:
-Subkritisch Laminair: NR < 500 y NF. < 1
-Turbulent subkritisch: N.R > 2000 en NF. < 1
-Superkritische laminaire: NR < 500 y NF. > 1
-Superkritisch turbulent: NR > 2000 en NF. > 1
Wanneer de stromen in de overgangsregio's voorkomen, zijn deze vanwege hun instabiliteit moeilijker te karakteriseren.
Een rivier van 4 m breed en 1 m diep heeft een stroming van 3 m3 / s. Bepaal of de stroom subkritisch of superkritisch is.
Om de waarde van N te vindenF. het is vereist om de snelheid van de rivierstroom te kennen. De verklaring geeft ons het debiet, ook wel de volumestroom genoemd, dat afhangt van het dwarsdoorsnedegebied en de snelheid v van het debiet. Het wordt als volgt berekend:
Q = A.v
Waar Q is de stroom, NAAR is het dwarsdoorsnedegebied en v is de snelheid. Uitgaande van een rechthoekig dwarsdoorsnedegebied:
A = breedte x diepte = 4 m x 1 m = 4 mtwee
Dan is de snelheid v:
v = Q / A = 3 m3 / s / 4 mtwee= 0,75 m / s
De hydraulische diepte in het geval van de buis met rechthoekige doorsnede valt samen met de diepte en vervangt daarom waarden in de vergelijking voor NF., met Yh = 1 m Y g = 9,8 m / stwee jij hebt:
NF. = v / (gyh ½ = 0,75 m / s / (9,8 m / stwee x 1 m) ½ = 0,24
Aangezien NF. kleiner is dan 1, heeft de stroom een subkritisch gedrag, dat wil zeggen langzaam.
Niemand heeft nog op dit artikel gereageerd.