
Kwantumnummers waar zijn ze voor en waarvoor zijn ze

De nKwantumgetallen worden gebruikt om de kwantumtoestand van de elektronen in het atoom te beschrijven en zijn afkomstig van de oplossing van de Schrödingervergelijking voor de eenvoudigste van allemaal: waterstof.
De Schrödingervergelijking is een differentiaalvergelijking, waarvan de oplossingen dat zijn golffuncties en worden aangeduid met de Griekse letter ψ. Er kunnen oneindige oplossingen worden voorgesteld, en hun kwadraat is gelijk aan de kans om het elektron te vinden in een klein gebied in de ruimte, genaamd orbitaal.
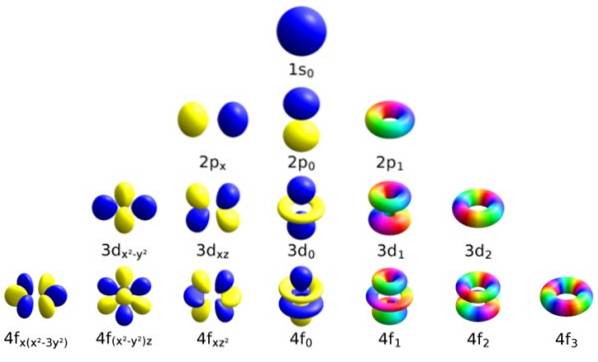
Elke baan heeft duidelijke kenmerken die hem onderscheiden van de andere, zoals energie, impulsmoment en spin, een volledig kwantumeigenschap van het elektron en die onder meer verantwoordelijk is voor magnetische effecten..
De manier om elke orbitaal te identificeren, is door deze te onderscheiden door een reeks getallen die hem beschrijven, en dit zijn precies de kwantumgetallen:
-n: is het belangrijkste kwantumgetal.
-ℓ: het azimutale kwantumgetal.
-mℓ, is het magnetische nummer.
-ms, het draai-nummer.
Artikel index
- 1 Waar zijn kwantumgetallen voor?
- 1.1 Wave-functies
- 2 Wat zijn kwantumgetallen?
- 2.1 Hoofdkwantumnummer
- 2.2 Azimutaal of impulsmoment kwantumgetal
- 2.3 Magnetisch kwantumgetal mℓ
- 2.4 Spin kwantumgetal ms
- 3 referenties
Waar zijn kwantumgetallen voor?
Kwantumgetallen worden gebruikt om de toestand van de elektronen in het atoom te beschrijven. Dat atomaire model waarin het elektron rond de kern draait, is onnauwkeurig, omdat het niet consistent is met atomaire stabiliteit of met een groot aantal waargenomen fysische verschijnselen.
Daarom deed de Deen Niels Bohr (1885-1962) in 1913 een gewaagd voorstel: het elektron is alleen te vinden in bepaalde stabiele banen, waarvan de grootte afhangt van een geheel getal genaamd n.
Later, in 1925, stelde de eveneens Oostenrijkse natuurkundige Erwin Schrödinger (1887-1961) een differentiaalvergelijking voor in partiële derivaten, waarvan de oplossingen het waterstofatoom beschrijven. Dit zijn de golffuncties ψ die in het begin werden genoemd.
Deze differentiaalvergelijking omvat de drie ruimtelijke coördinaten plus tijd, maar als deze niet wordt meegerekend, is de oplossing van de Schrödingervergelijking analoog aan die van een staande golf (een golf die zich voortplant tussen bepaalde grenzen).
Wave-functies
De tijdonafhankelijke Schrödingervergelijking wordt opgelost in sferische coördinaten en de oplossing wordt geschreven als het product van drie functies, één voor elke ruimtelijke variabele. In dit coördinatensysteem, in plaats van de coördinaten van de cartesische assen te gebruiken X, Y Y z de coördinaten worden gebruikt r, θ Y φ. Op deze manier:
ψ (r, θ, φ) = R (r) ⋅f (θ) ⋅g (φ)
De golffunctie is ongrijpbaar, maar de kwantummechanica vertelt ons dat de kwadratische amplitude:
| ψ (r, θ, φ) |twee
Dat wil zeggen, de modulus of absolute waarde van de golffunctie, in het kwadraat, is een reëel getal dat de kans vertegenwoordigt om het elektron te vinden, in een bepaald gebied rond het punt waarvan de coördinaten zijn r, θ Y φ.
En dit feit is iets concreets en tastbaars.
Om de golffunctie te vinden, moet je drie gewone differentiaalvergelijkingen oplossen, één voor elke variabele r, θ Y φ.
De oplossingen van elke vergelijking, die de functies R (r), f (θ) en g (φ) zullen zijn, bevatten de eerste drie genoemde kwantumgetallen.
Wat zijn kwantumgetallen?
Hieronder beschrijven we kort de aard van elk kwantumgetal. De eerste drie komen, zoals eerder vermeld, voort uit de oplossingen van de Schrödingervergelijking.
Het vierde nummer werd in 1928 toegevoegd door Paul Dirac (1902 - 1984).
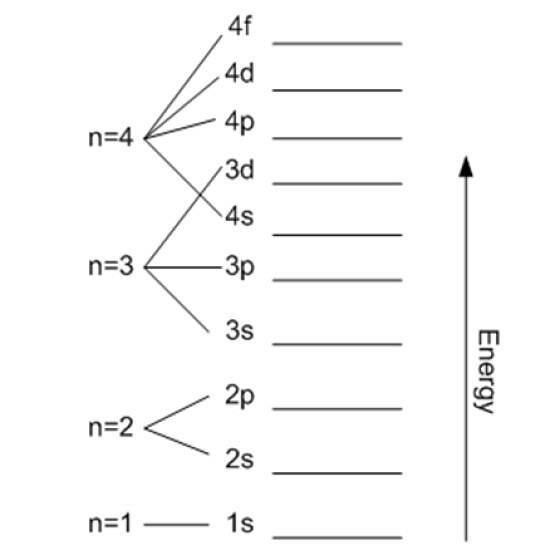
Hoofdkwantumnummer
Het wordt aangeduid met n en geeft de grootte van de toegestane orbitaal aan, evenals de energie van het elektron. Hoe hoger de waarde, hoe verder het elektron zich van de kern bevindt en de energie zal ook hoger zijn, maar in ruil daarvoor vermindert het de stabiliteit.
Dit getal komt voort uit de functie R (r), de kans om het elektron op een bepaalde afstand te vinden r van de kern, die wordt bepaald door:
-De constante van Planck: h = 6,626 × 10 -3. 4 J.s
-Elektronenmassa men = 9,1 × 10-31 kg
-Elektronenlading: e = 1,6 × 10-19 C.
-Elektrostatische constante: k = 9 × 10 9 N.mtwee/ Ctwee
Als n = 1 komt het overeen met de Bohr-straal die ongeveer 5,3 x 10 is-11 m.
Behalve de eerste laag, zijn de andere onderverdeeld in sublagen of subniveaus. Elke schaal heeft een energie in elektronvolt gegeven door:

- K (n = 1)
- L (n = 2)
- M (n = 3)
- N (n = 4)
- O (n = 5)
- P (n = 6)
- Q (n = 7).
In theorie is er geen bovengrens voor n, maar in de praktijk wordt opgemerkt dat deze alleen n = 8 bereikt. De laagst mogelijke energie komt overeen met n = 1 en is die van de fundamentele toestand.
Kwantumgetal van azimutaal of impulsmoment
Aangeduid met de cursieve letter ℓ, bepaalt dit getal de vorm van de orbitalen, door de grootte van het orbitale impulsmoment van het elektron te kwantificeren.
Het kan positieve en gehele getallen tussen 0 en n-1 aannemen, bijvoorbeeld:
-Als n = 1, dan is ℓ = 0 en is er maar één subniveau.
-Als n = 2, dan kan ℓ gelijk zijn aan 0 of 1, dus we hebben twee subniveaus.
-En als n = 3, dan neemt ℓ de waarden 0, 1 en 2 aan en zijn er 3 subniveaus.
Het kan op deze manier oneindig worden voortgezet, hoewel zoals eerder gezegd, in de praktijk n oploopt tot 8. De subniveaus worden aangeduid met de letters: s, p, d, F. Y g en ze nemen toe in energie.

Magnetisch kwantumgetal mℓ
Dit getal bepaalt de oriëntatie van de orbitaal in de ruimte en de waarde hangt af van die van ℓ.
Voor een gegeven ℓ zijn er (2ℓ + 1) gehele waarden van m ℓ, die overeenkomen met de respectieve orbitalen. Dit zijn:
-ℓ, (- ℓ + 1), ... 0, ... (+ ℓ -1), + ℓ.
Voorbeeld
Als n = 2, weten we dat ℓ = 0 en ℓ = 1, dan is m ℓ heeft de volgende waarden:
-Voor ℓ = 0: m ℓ = 0.
-Voor ℓ = 1: m ℓ = -1, m ℓ = 0, m ℓ = +1
De n = 2 orbitaal heeft twee subniveaus, het eerste met n = 2, ℓ = 0 en m ℓ = 0. Dan hebben we het tweede subniveau: n = 2, ℓ = 1, met 3 orbitalen:
- n = 2, ℓ = 1, m ℓ = -1
- n = 2, ℓ = 1, m ℓ = 0
- n = 2, ℓ = 1, m ℓ = +1
De drie orbitalen hebben dezelfde energie maar verschillende ruimtelijke oriëntatie.
Draai kwantumnummer ms
Bij het oplossen van de Schrödingervergelijking in drie dimensies komen de reeds beschreven getallen naar voren. Bij waterstof wordt echter een nog fijnere structuur waargenomen die deze getallen niet voldoende zijn om te verklaren.
Om deze reden stelde een andere natuurkundige, Wolfgang Pauli, in 1921 het bestaan van een vierde getal voor: het spinnummer ms, die waarden aanneemt van + ½ of -½.
Dit nummer beschrijft een zeer belangrijke eigenschap van het elektron, namelijk de spin, woord dat uit het engels komt spin (om zichzelf aan te zetten). En de spin is op zijn beurt gerelateerd aan de magnetische eigenschappen van het atoom.
Een manier om spin te begrijpen is door je voor te stellen dat het elektron zich gedraagt als een kleine magnetische dipool (een magneet met noord- en zuidpool), dankzij een rotatie om zijn eigen as. De rotatie kan in dezelfde richting zijn als met de klok mee, of in de tegenovergestelde richting.
Hoewel Pauli het bestaan van dit aantal suggereerde, hadden de resultaten van een experiment van Otto Stern en Walter Gerlach in 1922 er al op geanticipeerd..
Deze wetenschappers slaagden erin een bundel zilveratomen in tweeën te delen door een niet-uniform magnetisch veld aan te leggen.
De waarde van ms is niet afhankelijk van n, ℓ en m ℓ. In grafische vorm wordt het weergegeven door een pijl: een pijl omhoog geeft een draai met de klok mee en een pijl omlaag geeft een draai tegen de klok in.
Pauli-uitsluitingsprincipe
Het gedrag van elektronen in het atoom wordt samengevat in het Pauli-uitsluitingsprincipe, dat stelt dat twee elektronen in een atoom niet in dezelfde kwantumtoestand kunnen bestaan..
Daarom moet elk elektron een andere reeks kwantumgetallen n, ℓ, m hebben ℓ en Ms.
Het belang van kwantumgetallen en dit principe ligt in het begrijpen van de eigenschappen van de elementen in het periodiek systeem: elektronen worden georganiseerd in lagen volgens n, en vervolgens in sublagen volgens ℓ en de rest van de getallen.
Referenties
- Alonso, M. 1971. Kwantum- en statistische grondslagen. Inter-Amerikaans educatief fonds.
- Bauer, W. 2011. Physics for Engineering and Sciences. Deel 1. Mc Graw Hill.
- Chang, R. 2013. Chemistry. 11e. Editie. Mc Graw Hill Education.
- Eisberg-Resnick. 1989. Quantum Physics. Limusa - Wiley.
- Giambattista, A. 2010. Physics. 2e. Ed McGraw Hill.
- Rex, A. 2011. Fundamentals of Physics. Pearson.
- Tippens, P. 2011. Fysica: concepten en toepassingen. 7e editie. Mcgraw heuvel.

Niemand heeft nog op dit artikel gereageerd.