EEN perfect getal is een natuurlijk getal zodat de som van de delers is hetzelfde als het aantal. Het is duidelijk dat het nummer zelf niet tussen de delers kan worden opgenomen.
Een van de eenvoudigste voorbeelden van een perfect getal is 6, aangezien de delers: 1, 2 en 3 zijn. Als we de delers optellen, krijgen we: 1 + 2 + 3 = 6.
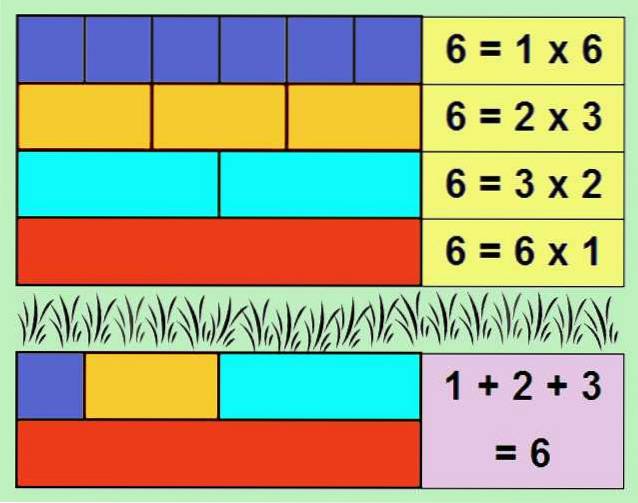
De som van de delers van een geheel getal, het getal zelf niet meegerekend, wordt aangeroepen aliquot. Daarom is een perfect getal gelijk aan zijn aliquot.
Maar als het getal zelf is opgenomen in de som van delers van een getal, dan is een perfect getal er een dat de som van al zijn delers gedeeld door 2 gelijk is aan het getal zelf..
Artikel index
Wiskundigen uit de oudheid, met name de Grieken, hechtten veel belang aan volmaakte getallen en schreven hen goddelijke eigenschappen toe..
Zo bevestigde Philo van Alexandrië tegen de eerste eeuw dat 6 en 28 perfecte getallen zijn die samenvallen met de zes dagen van de schepping van de wereld en de achtentwintig dagen die nodig zijn voordat de maan rond de aarde gaat..
Perfecte getallen zijn ook aanwezig in de natuur, zo verschijnt aan de noordpool van Saturnus ook het volmaakte getal 6, een zeshoekige draaikolk gevonden door de Cassini-sonde en dat heeft wetenschappers geïntrigeerd..
De honingraten van bijen hebben cellen in een zeshoekige vorm, dat wil zeggen met 6 zijden. Het is aangetoond dat de veelhoek met het perfecte getal 6 degene is die het mogelijk maakt het aantal cellen in de bijenkorf te maximaliseren, met een minimum aan was voor de uitwerking ervan..
De som van alle delers van een natuurlijk getal n wordt aangegeven met σ (n). In een perfect getal is voldaan dat: σ (n) = 2n.
Euclides ontdekte een formule en een criterium waarmee je de perfecte getallen kunt vinden. Deze formule is:
twee(n-1) (tween -1)
Het getal dat door de formule wordt gegenereerd, is echter alleen perfect als de factor (2n -1) wees een neef.
Laten we eens kijken hoe de eerste perfecte getallen worden gegenereerd:
Als n = 2 dan houden we 2 over1 (tweetwee - 1) = 2 x 3 = 6 die we al zagen is perfect.
Als n = 3 hebben we 2twee (twee3 - 1) = 4 x 7 = 28 wat ook perfect is zoals in detail geverifieerd in voorbeeld 1.
Laten we eens kijken wat er gebeurt met n = 4. Bij het vervangen in de formule van Euclides hebben we:
twee3 (twee4 - 1) = 8 x 15 = 120
Er kan worden geverifieerd dat dit getal niet perfect is, zoals in detail wordt weergegeven in Voorbeeld 3. Dit is niet in tegenspraak met het criterium van Euclides, aangezien 15 geen priemgetal is, een noodzakelijke vereiste voor het resultaat om een perfect getal te zijn..
Laten we nu eens kijken wat er gebeurt als n = 5. Door de formule toe te passen die we hebben:
twee4 (twee5 - 1) = 16 x 31 = 496
Aangezien 31 een priemgetal is, moet het getal 496 perfect zijn, volgens de criteria van Euclides. In voorbeeld 4 wordt in detail getoond dat dit inderdaad het geval is.
Priemgetallen met de vorm 2p - 1 worden Mersenne-neven genoemd, naar de monnik Marin Mersenne, die in de 17e eeuw priemgetallen en perfecte getallen bestudeerde..
Later in de 18e eeuw toonde Leonhard Euler aan dat alle perfecte getallen gegenereerd door de formule van Euclides even zijn.
Tot op heden is er geen perfectie gevonden die vreemd is.
Tot op heden zijn 51 perfecte getallen bekend, allemaal gegenereerd door de formule en het criterium van Euclides. Dit nummer werd verkregen toen de grotere neef van Mersenne werd gevonden, namelijk: (282589933 - 1).
Het perfecte nummer # 51 is (282589933) x (282589933 - 1) en heeft 49724095 cijfers.
In de getaltheorie wordt gezegd dat twee getallen vrienden zijn wanneer de som van de delers van één, het getal zelf niet meegerekend, gelijk is aan het andere getal en vice versa.
De lezer kan verifiëren dat de som van de delers van 220, exclusief 220, 284 is. Aan de andere kant is de som van de delers van 284, exclusief 284, gelijk aan 220. Daarom zijn de getallen 220 en 284 vrienden.
Vanuit dit oogpunt is een perfect aantal vrienden met zichzelf..
De eerste acht perfecte getallen staan hieronder vermeld:
6
28
496
8128
33550336
8589869056
137438691328
2305843008139952128
In de volgende oefeningen is het nodig om de delers van een getal te berekenen, ze vervolgens op te tellen en te controleren of het getal een perfect getal is of niet..
Daarom zullen we, voordat we de oefeningen benaderen, het concept bekijken en laten zien hoe ze worden berekend..
Om te beginnen moet je onthouden dat getallen priemgetallen kunnen zijn (wanneer ze alleen exact met zichzelf en 1 kunnen worden gedeeld) of samengesteld (wanneer ze kunnen worden ontleed als een product van priemgetallen).
Voor een samengesteld getal N hebben we:
N = eenn . bm. cp ... rk
Waar a, b, c ... r priemgetallen zijn en n, m, p ... k exponenten zijn die behoren tot de natuurlijke getallen, die vanaf 1 kunnen zijn.
In termen van deze exponenten is er een formule om te weten hoeveel delers het getal N heeft, hoewel het ons niet vertelt wat deze zijn. Laat C deze hoeveelheid zijn, dan:
C = (n +1) (m + 1) (p +1)… (k + 1)
Door het getal N te ontleden als een product van priemgetallen en te weten hoeveel delers het heeft, zowel priemgetallen als niet-priemgetallen, kunnen we bepalen wat deze delers zijn..
Als je ze allemaal hebt, behalve de laatste die niet vereist is in de som, kun je controleren of het een perfect getal is of niet.
Controleer of het nummer 28 perfect is.
Het eerste ding zal zijn om het getal op te splitsen in zijn belangrijkste factoren.
28 | 2
14 | 2
07 | 7
01 | 1
De delers zijn: 1, 2, 4, 7, 14 en 28. Als we 28 uitsluiten, geeft de som van de delers:
1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28
Daarom is 28 een perfect getal.
Bovendien is de som van al zijn delers 28 + 28, dus aan de regel σ (28) = 2 x 28 is voldaan.
Beslissen of het getal 38 perfect is of niet.
Het aantal wordt opgesplitst in de belangrijkste factoren:
39 | 3
13 | 13
01 | 1
De delers van 39 zonder het getal zelf op te nemen zijn: 1, 3 en 13. De som 1 + 3 + 13 = 4 + 13 = 17 is niet gelijk aan 39, daarom is 39 een onvolmaakt of niet-perfect getal.
Zoek uit of nummer 120 perfect of onvolmaakt is.
We gaan verder met het opsplitsen van het aantal in de belangrijkste factoren:
120 | 2
060 | 2
30 | 2
15 | 3
5 | 5
1 | 1
Van de belangrijkste factoren gaan we verder om de delers te vinden:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 en 120
Als 120 perfect was, zou het optellen van al zijn delers 2 x 120 = 240 moeten opleveren.
1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360
Dit resultaat is duidelijk anders dan 240, dus er wordt geconcludeerd dat het getal 120 geen perfect getal is..
Controleer of het getal 496, verkregen door het criterium van Euclides, een perfect getal is.
Het getal 496 is opgesplitst in de belangrijkste factoren:
496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1
Dus zijn delers zijn:
1, 2, 4, 8, 16, 31, 62, 124, 248, 496
Nu zijn ze allemaal toegevoegd, behalve 496:
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496
Bevestigend dat het inderdaad een perfect getal is.
Niemand heeft nog op dit artikel gereageerd.