
Omtrek van de cirkel hoe het eruit te halen en formules, opgeloste oefeningen

De cirkel omtrek is de verzameling punten die de omtrek van een cirkel vormen en wordt ook wel lengte van de omtrek. Het hangt af van de straal, aangezien een grotere omtrek uiteraard een grotere omtrek zal hebben.
Worden P. de omtrek van een cirkel en R de straal ervan, dan kunnen we berekenen P. met de volgende vergelijking:
P = 2π.R

Waar π een reëel getal is (lees "pi") dat ongeveer 3,1416 waard is ... De ellips is te wijten aan het feit dat π oneindig veel decimalen heeft. Daarom is het bij het maken van berekeningen noodzakelijk om de waarde ervan af te ronden.
Voor de meeste toepassingen is het echter voldoende om het hier aangegeven bedrag te nemen, of alle decimalen te gebruiken die de rekenmachine waarmee u werkt, retourneert..
Als het in plaats van de straal de voorkeur heeft om de diameter D te gebruiken, waarvan we weten dat deze tweemaal de straal is, wordt de omtrek als volgt uitgedrukt:
P = π.2R = π.D
Omdat de omtrek een lengte is, moet deze altijd worden uitgedrukt in eenheden zoals meters, centimeters, voeten, inches en meer, afhankelijk van het systeem dat de voorkeur heeft..
Artikel index
- 1 Omtrekken en cirkels
- 2 Demonstratie-oefeningen voor het berekenen van de omtrek van de cirkel
- 2.1 - Oefening 1
- 2.2 - Oefening 2
- 2.3 - Oefening 3
- 3 Toepassingen
- 4 referenties
Omtrekken en cirkels
Dit zijn vaak termen die door elkaar worden gebruikt, dat wil zeggen synoniem. Maar het komt voor dat er verschillen tussen hen zijn.
Het woord "omtrek" komt van het Griekse "peri" wat contour en "meter" of maat betekent. De omtrek is de omtrek of omtrek van de cirkel. Formeel wordt het als volgt gedefinieerd:
Een cirkel is de verzameling punten met gelijke afstand tot een punt dat het middelpunt wordt genoemd, deze afstand is de straal van de omtrek.
Van zijn kant wordt de cirkel als volgt gedefinieerd:
Een cirkel is de verzameling punten waarvan de afstand tot een punt dat het middelpunt wordt genoemd, is Minder dan of gelijk op een vaste afstand genaamd radio.
De lezer kan het subtiele verschil tussen de twee concepten zien. De omtrek verwijst alleen naar de reeks punten van de rand, terwijl de cirkel de reeks punten is van de rand naar het interieur, waarvan de omtrek de grens is.
Opdrachten ddemonstratie van het berekenen van de omtrek van de cirkel
Door middel van de volgende oefeningen zullen de hierboven beschreven concepten in praktijk worden gebracht, evenals enkele andere die zullen worden uitgelegd zodra ze verschijnen. We beginnen met de eenvoudigste en de moeilijkheidsgraad zal geleidelijk toenemen.
- Oefening 1
Zoek de omtrek en de oppervlakte van de cirkel met een straal van 5 cm.
Oplossing
De vergelijking die aan het begin is gegeven, wordt direct toegepast:
P. = 2π.R= 2π,5 cm = 10 π cm = 31.416 cm
Om de oppervlakte te berekenen NAAR de volgende formule wordt gebruikt:
NAAR π.Rtwee π. (5 cm)twee= 25π cmtwee= 78,534 cmtwee
- Oefening 2
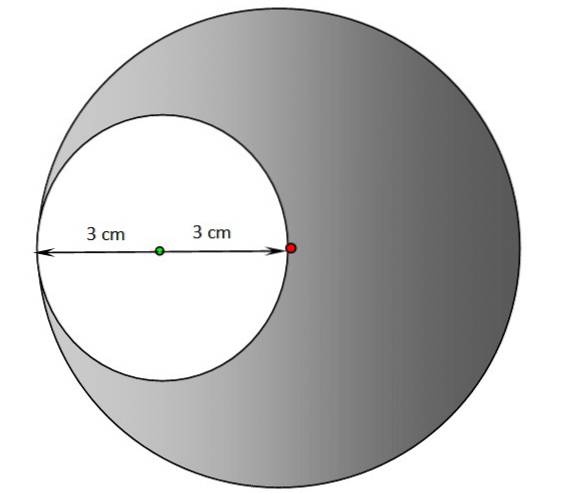
a) Zoek de omtrek en het gebied van het lege gebied in de volgende afbeelding. Het midden van de gearceerde cirkel bevindt zich op het rode punt, terwijl het midden van de witte cirkel het groene punt is.
b) Herhaal het vorige gedeelte voor het gearceerde gebied.
Oplossing
a) De straal van de witte cirkel is 3 cm, daarom passen we dezelfde vergelijkingen toe als in oefening 1:
P. = 2π.R= 2π,3 cm = 6 π cm = 18,85 cm
NAAR π.Rtwee π. (3 cm)twee= 9π cmtwee= 28,27 cmtwee
b) Voor de gearceerde cirkel is de straal 6 cm, de omtrek is het dubbele van die berekend in sectie a):
P. = 2π.R= 2π,6 cm = 12 π cm = 37,70 cm
En tot slot wordt het gebied van het gearceerde gebied als volgt berekend:
- Eerst vinden we het gebied van de gearceerde cirkel alsof deze compleet is, die we A 'zullen noemen, zoals dit:
NAAR' π.Rtwee= π. (6 cm)twee = 36π cmtwee= 113,10 cmtwee
- Dan naar het gebied NAAR' De oppervlakte van de witte cirkel wordt afgetrokken, eerder berekend in sectie a), op deze manier wordt de gevraagde oppervlakte verkregen, die eenvoudig wordt aangeduid als A:
A = A '- 28,27 cmtwee = 113,10-28,27 cmtwee = 84,83 cmtwee
- Oefening 3
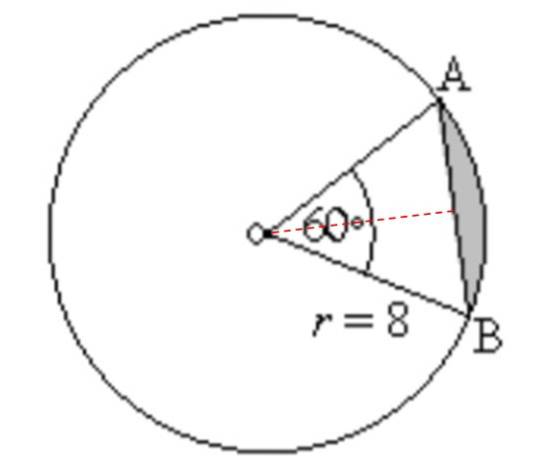
Zoek het gebied en de omtrek van het gearceerde gebied in de volgende afbeelding:
Oplossing
Berekening van de oppervlakte van het gearceerde gebied
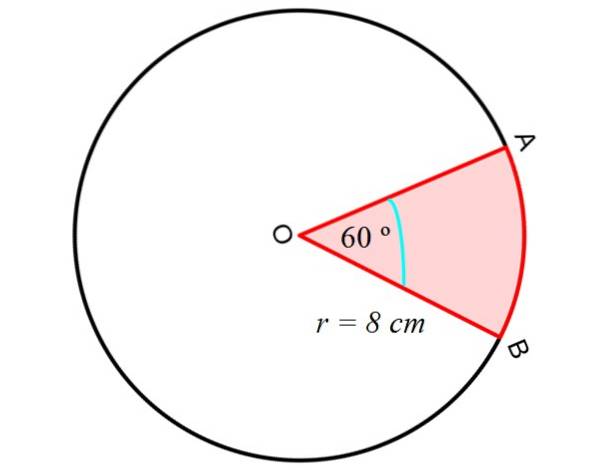
We berekenen eerst de oppervlakte van circulaire sector of wig, tussen de rechte segmenten OA en OB en het cirkelsegment AB, zoals weergegeven in de volgende afbeelding:
Hiervoor wordt de volgende vergelijking gebruikt, die ons de oppervlakte van een cirkelvormige sector geeft, met kennis van de straal R en de centrale hoek tussen de segmenten OA en OB, dat wil zeggen twee van de stralen van de omtrek:
NAAR circulaire sector = Π.Rtwee. (αº / 360º)
Waar αº de centrale hoek is -het is centraal omdat de top het midden van de omtrek is- tussen twee stralen.
Stap 1: bereken de oppervlakte van de circulaire sector
Het gebied van de sector dat in de afbeelding wordt weergegeven, is dus:
NAAR circulaire sector = Π.Rtwee. (αº / 360º) = π. (8 cmtwee. (60º / 360º) = (64/6) π cmtwee= 33,51 cmtwee
Stap 2: bereken de oppervlakte van de driehoek
Vervolgens berekenen we de oppervlakte van de witte driehoek in figuur 3. Deze driehoek is gelijkzijdig en de oppervlakte is:
NAAR driehoek = (1/2) basis x hoogte
De hoogte is de rode stippellijn in figuur 4. Om deze te vinden kun je bijvoorbeeld de stelling van Pythagoras gebruiken. Maar het is niet de enige manier.
De oplettende lezer zal hebben opgemerkt dat de gelijkzijdige driehoek is verdeeld in twee identieke rechthoekige driehoeken, waarvan de basis 4 cm is:
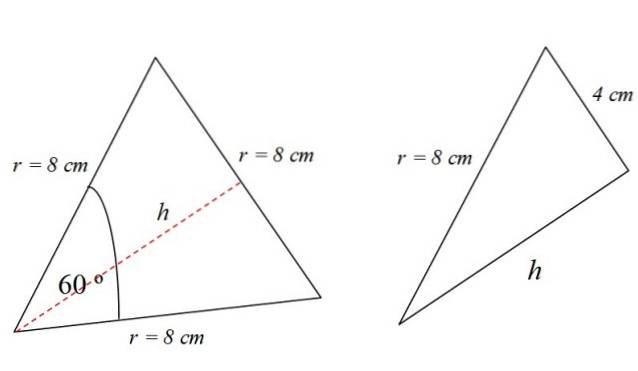
In een rechthoekige driehoek is aan de stelling van Pythagoras voldaan, dus:

NAAR driehoek = (1/2) basis x hoogte = (1/2) 8 cm x 6,93 cm = 27,71 cmtwee.
Stap 3: het gearceerde gebied berekenen
Het is voldoende om het grotere gebied (dat van de cirkelvormige sector) af te trekken van het kleinere gebied (dat van de gelijkzijdige driehoek): A gearceerd gebied 33,51 cmtwee - 27,71 cmtwee = 5,80 cmtwee.
Berekening van de omtrek van het gearceerde gebied
De gezochte omtrek is de som van de rechtlijnige zijde van 8 cm en de boog van omtrek AB. Nu, de volledige omtrek onderspant 360 °, daarom is een boog die 60 ° onderspant een zesde van de volledige lengte, waarvan we weten dat deze 2.π.R is:
AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm
Vervanging, de omtrek van het gearceerde gebied is:
P = 8 cm + 8,38 cm = 16,38 cm.
Toepassingen
De omtrek is, net als het gebied, een zeer belangrijk concept in de geometrie en met veel toepassingen in het dagelijks leven..
Kunstenaars, ontwerpers, architecten, ingenieurs en vele andere mensen maken gebruik van de omtrek tijdens het ontwikkelen van hun werk, vooral dat van een cirkel, aangezien de ronde vorm overal is: van reclame, via voedsel tot machines.

Om de lengte van een omtrek direct te kennen, volstaat het om deze met een draad of touwtje om te wikkelen, deze draad vervolgens te verlengen en te meten met een meetlint. Het andere alternatief is om de straal of diameter van de cirkel te meten en een van de hierboven beschreven formules te gebruiken..
In het dagelijkse werk wordt het concept van omtrek gebruikt wanneer:
-Voor een bepaalde maat pizza of cake wordt de juiste vorm gekozen.
-Er zal een stedelijke weg worden ontworpen door de grootte van een libel te berekenen waar auto's kunnen draaien om van richting te veranderen.
-We weten dat de aarde rond de zon draait in een ongeveer cirkelvormige baan - planeetbanen zijn eigenlijk elliptisch, volgens de wetten van Kepler - maar de omtrek is een zeer goede benadering voor de meeste planeten..
-De juiste maat van een ring wordt gekozen om in een online winkel te kopen.
-We kiezen een sleutel van de juiste maat om een moer los te draaien.
En nog veel meer.
Referenties
- Gratis wiskundehandleidingen. Oppervlakte en omtrek van een cirkel - Geometriecalculator. Hersteld van: analyzemath.com.
- Math Open Reference. Omtrek, omtrek van een cirkel. Hersteld van: mathopenref.com.
- Monterey Institute. Omtrek en gebied. Hersteld van: montereyinstitute.org.
- Wetenschappelijk. Hoe de omtrek van een cirkel te vinden. Hersteld van: sciencing.com.
- Wikipedia. Omtrek. Hersteld van: en.wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.