De elektrisch potentieel het wordt op elk punt waar een elektrisch veld bestaat gedefinieerd als de potentiële energie van dat veld per eenheidslading. Puntladingen en punt- of continue ladingsverdelingen produceren een elektrisch veld en hebben daarom een bijbehorend potentieel.
In het International System of Units (SI) wordt het elektrische potentieel gemeten in volt (V) en wordt het aangeduid als V.Wiskundig wordt het uitgedrukt als:
V = U / qof
Waar U de potentiële energie is die verband houdt met de lading of distributie en qof het is een positieve testlading. Aangezien U een scalair is, is dat ook het potentieel.
Volgens de definitie is 1 volt gewoon 1 Joule / Coulomb (J / C), waarbij Joule de SI-eenheid voor energie is en Coulomb (C) de eenheid voor elektrische lading..
Stel dat een puntlading q. We kunnen de aard van het veld dat deze lading produceert, controleren door een kleine, positieve testlading te gebruiken, genaamd qof, gebruikt als sonde.
Het werk dat W nodig had om deze kleine last van het punt te verplaatsen naar tot het punt b, is het negatief van het verschil van potentiële energie ΔU tussen deze punten:
W.een → b = -ΔU = - (Ub - OFnaar
Alles verdelen tussen qof
W.een → b / qof= - ΔU / qof = - (Ub - OFnaar) / qof = - (Vb - V.naar) = -ΔV
Hier Vb is het potentieel op punt b en Vnaar is dat van punt a. Het potentiële verschil Vnaar - V.b is het potentieel van ongeveer b en heet Vab. De volgorde van de abonnementen is belangrijk, als deze zou worden gewijzigd, zou dit het potentieel van b met betrekking tot a.
Artikel index
Uit het voorgaande volgt dat:
-AV = Ween → b / qof
Daarom:
AV = -Ween → b / qof
Nu wordt het werk berekend als de integraal van het scalaire product tussen de elektrische kracht F. tussen q en qof en de verplaatsingsvector dℓ tussen de punten a en b. Aangezien het elektrische veld kracht per ladingeenheid is:
EN F./ qof
Het werk om de testbelasting van a naar b te dragen is:
Deze vergelijking biedt de manier om het potentiaalverschil direct te berekenen als het elektrische veld van de lading of de verdeling die het produceert eerder bekend is..
En er wordt ook opgemerkt dat het potentiaalverschil een scalaire grootheid is, in tegenstelling tot het elektrische veld, dat een vector is.
Uit de vorige definitie zien we dat if EN en dℓ loodrecht staan, is het potentiaalverschil ΔV nul. Dit betekent niet dat het potentieel op dergelijke punten nul is, maar dat gewoon Vnaar = Vb, dat wil zeggen, het potentieel is constant.
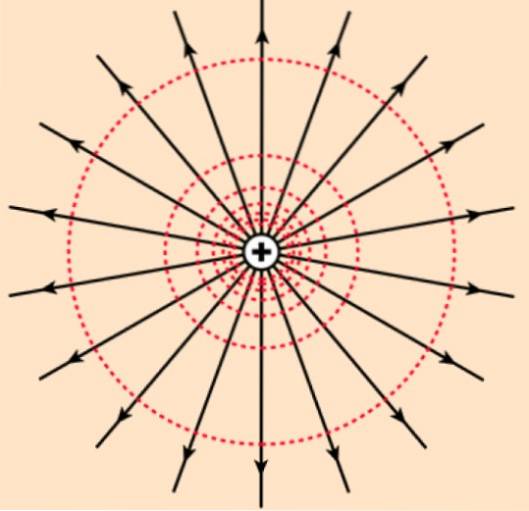
De lijnen en vlakken waar dit gebeurt, worden genoemd equipotentiaal. De equipotentiaallijnen van het veld van een puntlading zijn bijvoorbeeld omtrekken concentrisch met de lading. En de equipotentiaalvlakken zijn concentrische bollen.
Als het potentieel wordt geproduceerd door een positieve lading, waarvan het elektrische veld bestaat uit radiale lijnen die de lading projecteren, zal het potentieel steeds kleiner worden als we ons van het veld verwijderen. Als testbelasting qof positief is, voelt u minder elektrostatische afstoting naarmate u verder van u verwijderd bent q.
Integendeel, als de belasting wat negatief is, de testlading qof (positief) zal een lager potentieel hebben naarmate het dichter bij komt wat.
De hierboven gegeven integraal dient om het potentiaalverschil te vinden, en dus het potentieel op een bepaald punt b, als het referentiepotentiaal op een ander punt bekend is naar.
Er is bijvoorbeeld sprake van een puntbelasting wat, waarvan de elektrische veldvector op een punt op een afstand ligt r van de lading is:
EN = kq / rtwee r
Waar k is de elektrostatische constante waarvan de waarde in internationale systeemeenheden is:
k = 9 x 10 9 Nmtwee / Ctwee.
En de vector r is de eenheidsvector langs de verbindingslijn wat met punt P.
Het is vervangen in de definitie van AV
Dat punt kiezen b op afstand zijn r van de lading en dat wanneer a → ∞ de potentiaal 0 is, dan Vnaar = 0 en de vorige vergelijking is als:
V = kq / r
Kies V.naar = 0 wanneer a → ∞ zinvol is, omdat het op een punt ver van de belasting moeilijk te zien is dat het bestaat.
Als er veel puntladingen zijn verdeeld in een regio, wordt het elektrische potentieel dat ze produceren op elk punt P in de ruimte berekend, waarbij de individuele potentialen worden opgeteld die elk van hen produceert. A) Ja:
V = V1 + V.twee + V.3 +… VN = ∑ Vik
De sommatie strekt zich uit van i = tot N en het potentieel van elke lading wordt berekend met behulp van de vergelijking die in de vorige sectie is gegeven.
Uitgaande van het potentieel van een puntlading, kunnen we het potentieel vinden dat wordt geproduceerd door een geladen object, met een meetbare grootte, op elk punt P.
Om dit te doen, wordt het lichaam verdeeld in vele kleine oneindig kleine ladingen dq. Elk draagt bij aan het volledige potentieel met een dV oneindig klein.
Vervolgens worden al deze bijdragen opgeteld via een integraal en zo wordt het totale potentieel verkregen:
Er is elektrisch potentieel in verschillende apparaten waardoor het mogelijk is om elektrische energie te verkrijgen, bijvoorbeeld batterijen, autoaccu's en stopcontacten. Elektrische potentialen worden ook in de natuur tot stand gebracht tijdens elektrische stormen.
In cellen en batterijen wordt elektrische energie opgeslagen door chemische reacties erin. Deze treden op wanneer het circuit gesloten is, waardoor gelijkstroom kan stromen en een gloeilamp gaat branden of de startmotor van de auto kan werken..
Er zijn verschillende spanningen: 1,5 V, 3 V, 9 V en 12 V komen het meest voor.
Apparaten en apparaten die op commerciële wisselstroom werken, zijn aangesloten op een verzonken stopcontact. Afhankelijk van de locatie kan de spanning 120 V of 240 V zijn.
Het is degene die optreedt tijdens elektrische stormen, vanwege de beweging van elektrische lading door de atmosfeer. Het kan in de orde van 10 zijn8 V..
Dankzij een rubberen transportband wordt wrijvingslading geproduceerd, die zich ophoopt op een geleidende bol bovenop een isolerende cilinder. Dit genereert een potentiaalverschil dat enkele miljoenen volt kan bedragen.
In het hart bevinden zich gespecialiseerde cellen die polariseren en depolariseren, waardoor potentiële verschillen ontstaan. Deze kunnen door middel van een elektrocardiogram als functie van de tijd worden gemeten..
Deze eenvoudige test wordt uitgevoerd door elektroden op de borst van de persoon te plaatsen die kleine signalen kunnen meten..
Omdat het zeer lage spanningen zijn, moet u ze gemakkelijk versterken en ze vervolgens opnemen op een papieren tape of ze bekijken via de computer. De arts analyseert de pulsen op afwijkingen en spoort zo hartproblemen op.
De elektrische activiteit van de hersenen kan ook worden geregistreerd met een vergelijkbare procedure, een EEG genaamd..
Een lading Q = - 50,0 nC bevindt zich op 0,30 m vanaf het punt NAAR en 0,50 m vanaf punt B, zoals weergegeven in de volgende afbeelding. Beantwoord de volgende vragen:
a) Wat is het potentieel in A geproduceerd door deze lading?
b) En wat is het potentieel in B?
c) Als een lading q van A naar B beweegt, wat is dan het potentiaalverschil waardoor hij beweegt?
d) Neemt het potentieel ervan toe of af, volgens het vorige antwoord??
e) Als q = - 1,0 nC, wat is dan de verandering in zijn elektrostatische potentiële energie terwijl deze van A naar B beweegt??
f) Hoeveel werk doet het door Q geproduceerde elektrische veld als de testlading van A naar B beweegt?
Q is een puntlading, daarom wordt het elektrische potentieel in A berekend door:
V.NAAR = kQ / rNAAR = 9 x 109 x (-50 x 10-9) / 0,3 V = -1500 V
Op dezelfde manier
V.B. = kQ / rB. = 9 x 109 x (-50 x 10-9) / 0,5 V = -900 V
AV = Vb - V.naar = -900 - (-1500) V = + 600 V
Als de lading q positief is, neemt zijn potentiaal toe, maar als hij negatief is, neemt zijn potentiaal af.
ΔV = ΔU / qof → ΔU = qof AV = -1,0 x 10-9 x 600 J = -6,0 x 10-7 J.
Het minteken in AU geeft aan dat de potentiële energie in B kleiner is dan die van A.
Aangezien W = -ΔU realiseert het veld zich +6,0 x 10-7 J van werk.
Niemand heeft nog op dit artikel gereageerd.