
Lineair programmeren waarvoor het is, modellen, beperkingen, toepassingen
De lineair programmeren is een wiskundige methode die wordt gebruikt om een functie te optimaliseren (maximaliseren of minimaliseren zoals vereist) waarvan de variabelen aan beperkingen onderhevig zijn, zolang de functie en de beperkingen lineair afhankelijk zijn van de variabelen.
Over het algemeen modelleert de te optimaliseren functie een praktische situatie, zoals de winst van een fabrikant wiens inputs, arbeid of machines beperkt zijn.

Een van de eenvoudigste gevallen is die van een lineaire functie die moet worden gemaximaliseerd, die alleen afhangt van twee variabelen, genaamd beslissingsvariabelen. Het kan de volgende vorm hebben:
Z = k1x + ktweeY
Met k1 en ktwee constante. Deze functie staat bekend als de Objectieve functie. Natuurlijk zijn er situaties die meer dan twee variabelen verdienen om te studeren, omdat ze complexer zijn:
Z = k1X1 + ktweeXtwee + k3X3 + .
En de beperkingen worden ook wiskundig gemodelleerd door een systeem van vergelijkingen of ongelijkheden, even lineair in X en Y.
De reeks oplossingen van dit systeem wordt genoemd haalbare oplossingen of haalbare punten. En onder de haalbare punten is er ten minste één die de doelfunctie optimaliseert.
Lineaire programmering werd onafhankelijk ontwikkeld door de Amerikaanse natuurkundige en wiskundige George Dantzig (1914-2005) en de Russische wiskundige en econoom Leonid Kantorovich (1912-1986), kort na de Tweede Wereldoorlog..
De methode voor probleemoplossing die bekend staat als simplex-methode Het is het geesteskind van Dantzig, die werkte voor de Amerikaanse luchtmacht, de University of Berkeley en Stanford University.

Artikel index
- 1 Lineaire programmeermodellen
- 2 Modelvoorbeeld
- 3 Oplossingsmethoden
- 3.1 - Grafische of geometrische methode
- 3.2 - De simplex-methode van Dantzig
- 4 Toepassingen
- 5 oefeningen opgelost
- 5.1 - Oefening 1
- 5.2 - Oefening 2
- 6 referenties
Lineaire programmeermodellen
De elementen die nodig zijn om een lineair programmeermodel op te stellen, geschikt voor een praktijksituatie, zijn:
-Objectieve functie
-Beslissingsvariabelen
-Beperkingen
In de doelfunctie definieer je wat je wilt bereiken. Stel dat u uw winst uit de vervaardiging van bepaalde producten wilt maximaliseren. Vervolgens wordt de "winst" -functie vastgesteld, volgens de prijs waartegen de producten worden verkocht.
In wiskundige termen kan deze functie worden afgekort met de sommatie-notatie:
Z = ∑kik Xik
In deze vergelijking, kik zijn coëfficiënten en xik zijn de beslissingsvariabelen.
De beslissingsvariabelen zijn de elementen van het systeem waarvan de controle wordt uitgeoefend en hun waarden zijn positieve reële getallen. In het voorgestelde voorbeeld zijn de beslissingsvariabelen de hoeveelheid van elk product dat moet worden vervaardigd om de maximale winst te behalen.
Ten slotte hebben we de beperkingen, die lineaire vergelijkingen of ongelijkheden zijn in termen van de beslissingsvariabelen. Ze beschrijven de beperkingen van het probleem, die bekend zijn en kunnen bijvoorbeeld de hoeveelheden grondstof zijn die bij de fabricage beschikbaar zijn..
Soorten beperkingen
U kunt een M aantal beperkingen hebben, beginnend bij j = 1 tot j = M. Wiskundig gezien zijn de beperkingen van drie soorten:
- NAARj = ∑ eenij . Xik
- B.j ≥ ∑ bij . Xik
- Cj ≤ ∑ cij . Xik
De eerste beperking is van het lineaire vergelijkingstype en betekent dat de waarde Aj, die bekend is, moet worden gerespecteerd.
De overige twee beperkingen zijn lineaire ongelijkheden en het betekent dat de B-waardenj en Cj, bekend, kunnen ze worden gerespecteerd of overschreden, wanneer het weergegeven symbool ≥ (groter dan of gelijk aan) of gerespecteerd of niet overschreden is, indien het symbool ≤ (kleiner dan of gelijk aan) is.
Model voorbeeld
De toepassingsgebieden zijn zeer divers, gaande van bedrijfskunde tot voeding, maar om de methode te begrijpen wordt hieronder een eenvoudig model van een praktijksituatie met twee variabelen voorgesteld..
Een plaatselijke banketbakkerij staat bekend om twee specialiteiten: de zwarte woudcake en de sacripantina-cake..
Bij de bereiding hebben ze eieren en suiker nodig. Voor het Zwarte Woud heb je 9 eieren en 500 g suiker nodig, terwijl je voor de sacripantine 8 eieren en 800 g suiker nodig hebt. De respectievelijke verkoopprijzen zijn $ 8 en $ 10.
Het probleem is: hoeveel cakes van elk type moet het gebak maken om de winst te maximaliseren, wetende dat het 10 kilo suiker en 144 eieren bevat?
Beslissingsvariabelen
De beslissingsvariabelen zijn "x" en "y", die reële waarden aannemen:
-x: het aantal zwarte woudtaarten
-en: de taarten van het sacripantina-type.
Beperkingen
De beperkingen worden gegeven door het feit dat het aantal cakes een positieve hoeveelheid is en dat er beperkte hoeveelheden grondstof zijn om ze te bereiden..
Daarom nemen deze beperkingen in wiskundige vorm de vorm aan:
- x ≥ 0
- en ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8 y ≤ 10
Beperkingen 1 en 2 vormen de niet-negativiteitstoestand eerder blootgelegd, en alle opgeworpen ongelijkheden zijn lineair. In restricties 3 en 4 staan de waarden die niet overschreden mogen worden: 144 eieren en 10 kg suiker.
Objectieve functie
Ten slotte is de objectieve functie de winst die wordt behaald bij de productie van "x" hoeveelheid zwarte woudkoekjes plus "y" hoeveelheid sacripantines. Het wordt gebouwd door de prijs te vermenigvuldigen met het aantal gemaakte cakes en voor elk type op te tellen. Het is een lineaire functie die we G (x, y) zullen noemen:
G = 8x + 10j
Oplossingsmethoden
De verschillende oplossingsmethoden omvatten grafische methoden, het simplex-algoritme en de interne puntmethode, om er maar een paar te noemen..
- Grafische of geometrische methode
Als je een probleem met twee variabelen hebt, zoals in de vorige sectie, bepalen de beperkingen een veelhoekig gebied in het vlak xy, bellen Haalbaar gebied of regio van levensvatbaarheid.
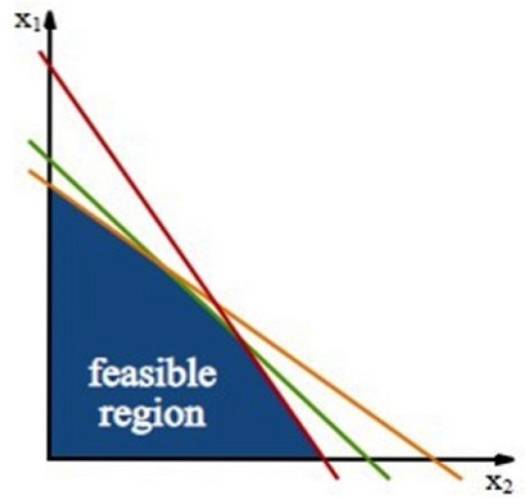
Deze regio is gebouwd door middel van restrictielijnen, dat zijn de lijnen die zijn verkregen uit de ongelijkheden van de beperkingen, die alleen werken met het gelijkheidsteken.
In het geval van de bakkerij die de winst wil optimaliseren, zijn de beperkende lijnen:
- x = 0
- y = 0
- 9x + 8y = 144
- 0,5 x + 0,8 jaar = 10
Alle punten in het gebied omsloten door deze lijnen zijn mogelijke oplossingen, dus er zijn er oneindig veel. Behalve in het geval dat het haalbare gebied leeg blijkt te zijn, dan heeft het gestelde probleem geen oplossing.
Gelukkig is voor het banketprobleem de haalbare regio niet leeg, we hebben het hieronder.
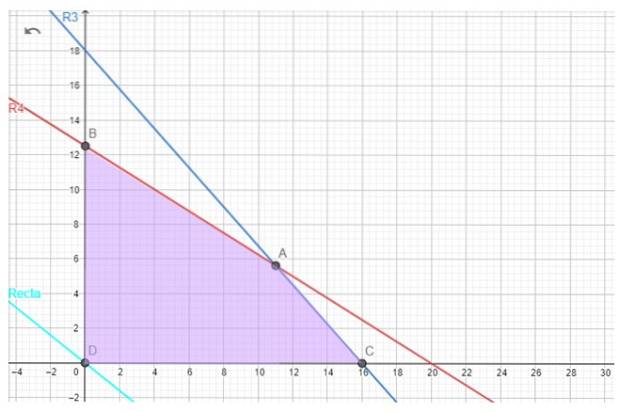
De optimale oplossing, indien die bestaat, wordt gevonden met behulp van de doelfunctie. Als we bijvoorbeeld proberen de maximale versterking G te vinden, hebben we de volgende regel, die wordt aangeroepen iso-profit lijn
G = k1x + ktweey → y = -k1x / ktwee + G / ktwee
Met deze lijn krijgen we alle paren (x, y) die een bepaalde versterking G geven, dus er is een familie van lijnen volgens de waarde van G, maar allemaal met dezelfde helling -k1 / ktwee, het zijn dus parallelle lijnen.
De optimale oplossing
Nu kan worden aangetoond dat de optimale oplossing van een lineair probleem altijd een extreem punt of hoekpunt van het haalbare gebied is. Dan:
De oplossingslijn is de lijn die het verst verwijderd is van de oorsprong en heeft ten minste één punt gemeen met de haalbare regio.
Als de lijn die het dichtst bij de oorsprong ligt een heel segment gemeen heeft met het haalbare gebied, wordt er gezegd dat er oneindig veel oplossingen zijn. Dit geval doet zich voor als de helling van de iso-profitlijn gelijk is aan die van een van de andere lijnen die de regio begrenzen.
Voor ons gebak zijn de kandidaat-hoekpunten A, B en C.
- De simplex-methode van Dantzig
De grafische of geometrische methode is van toepassing op twee variabelen. Het is echter ingewikkelder als er drie variabelen zijn en onmogelijk te gebruiken voor een groter aantal variabelen..
Bij problemen met meer dan twee variabelen, de simplex-methode, die bestaat uit een reeks algoritmen om de objectieve functies te optimaliseren. Matrices en eenvoudige rekenkunde worden vaak gebruikt om de berekeningen uit te voeren.
De simplex-methode begint met het kiezen van een haalbare oplossing en het controleren of deze optimaal is. Als dat het geval is, hebben we het probleem al opgelost, maar als dat niet het geval is, gaan we verder naar een oplossing die dichter bij optimalisatie ligt. Als de oplossing bestaat, vindt het algoritme deze in een paar pogingen.
Toepassingen
Lineaire en niet-lineaire programmering worden op veel gebieden toegepast om de beste beslissingen te nemen in termen van kostenverlaging en hogere winsten, die niet altijd in geld zijn, omdat ze in de tijd kunnen worden gemeten, bijvoorbeeld als u de benodigde tijd wilt minimaliseren om een reeks bewerkingen uit te voeren.
Hier zijn enkele velden:
-In marketing wordt het gebruikt om de beste combinatie van media (sociale netwerken, televisie, pers en andere) te vinden om reclame te maken voor een bepaald product.
-Voor het toewijzen van adequate taken aan het personeel van een bedrijf of fabriek of roosters aan hen.
-Bij de selectie van het meest voedzame voedsel en tegen de laagste kosten in de vee- en pluimvee-industrie.
Opgeloste oefeningen
- Oefening 1
Los grafisch het lineaire programmeermodel op dat in de voorgaande secties is opgeworpen.
Oplossing
Het is noodzakelijk om een grafiek te maken van de reeks waarden die is bepaald door het beperkingssysteem dat in de opgave is gespecificeerd:
- x ≥ 0
- en ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8 y ≤ 10
Het gebied gegeven door ongelijkheden 1 en 2 komt overeen met het eerste kwadrant van het cartesische vlak. Met betrekking tot ongelijkheden 3 en 4, beginnen we met het vinden van de restrictielijnen:
9x + 8y = 144
0,5 x + 0,8y = 10 → 5x + 8y = 100
Het haalbare gebied is een vierhoek waarvan de hoekpunten punten A, B, C en D zijn.
De minimumwinst is 0, daarom is de lijn 8x + 10y = 0 de ondergrens en hebben de iso-profitlijnen een helling van -8/10 = - 0,8.
Deze waarde verschilt van de hellingen van de andere restrictielijnen en aangezien het haalbare gebied begrensd is, bestaat de unieke oplossing.
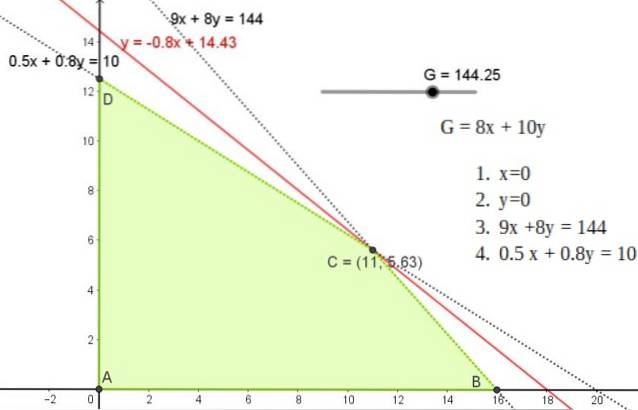
Deze oplossing komt overeen met een lijn met een helling van -0,8 die door een van de punten A, B of C loopt, waarvan de coördinaten zijn:
A (11; 5.625)
B (0; 12,5)
C (16, 0)
Optimale oplossing
We berekenen de waarde van G voor elk van deze punten:
-(11; 5.625): GNAAR = 8 x 11 + 10 x 5,625 = 144,25
-(0; 12,5): GB. = 8 x 0 + 10 x 12,5 = 125
-(16, 0): G.C = 8 x 16 + 10 x 0 = 128
De hoogste winst wordt behaald bij het vervaardigen van 11 zwarte woudkoekjes en 5.625 sacripantijnse koeken. Deze oplossing komt overeen met de oplossing die via de software is gevonden.
- Oefening 2
Controleer het resultaat van de vorige oefening door de Oplosser-functie te gebruiken die beschikbaar is in de meeste spreadsheets zoals Excel of LibreOffice Calc, die het Simplex-algoritme bevatten voor optimalisatie in lineair programmeren.
Oplossing
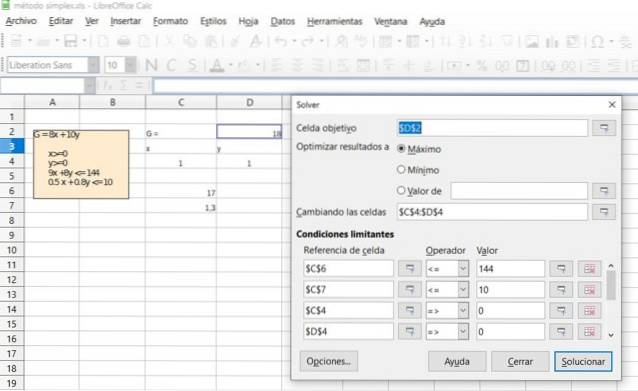
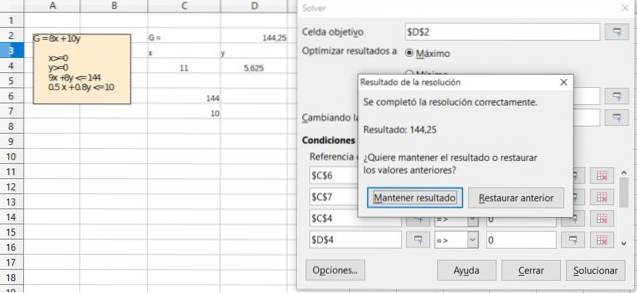
Referenties
- Briljant. Lineair programmeren. Hersteld van: brilliant.org.
- Eppen, G. 2000. Operationeel onderzoek in administratieve wetenschappen. 5e. Editie. Prentice hal.
- Haeussler, E. 1992. Wiskunde voor management en economie. 2e. Editie. Grupo Hoofdartikel Iberoamericana.
- Hiru.eus. Lineair programmeren. Hersteld van: hiru.eus.
- Wikipedia. Lineair programmeren. Hersteld van: es. wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.