
Mann's U-test - Whitney wat het is en wanneer het wordt toegepast, uitvoering, voorbeeld
De Mann-Whitney U-test Het wordt toegepast voor de vergelijking van twee onafhankelijke steekproeven wanneer ze weinig gegevens hebben of geen normale verdeling volgen. Op deze manier wordt het als een test beschouwd niet parametrisch, In tegenstelling tot zijn tegenhanger de Student's t-test, die wordt gebruikt als het monster groot genoeg is en de normale verdeling volgt.
Frank Wilcoxon stelde het voor het eerst voor in 1945, voor monsters van identieke afmetingen, maar twee jaar later werd het uitgebreid voor het geval van monsters van verschillende afmetingen door Henry Mann en D. R. Whitney..
De test wordt vaak toegepast om na te gaan of er een verband bestaat tussen een kwalitatieve en een kwantitatieve variabele.
Een illustratief voorbeeld is om een reeks hypertensieve mensen te nemen en twee groepen te extraheren, van wie de dagelijkse bloeddrukgegevens gedurende een maand worden geregistreerd.
Behandeling A wordt toegepast op de ene groep en behandeling B wordt toegepast op een andere groep. Hier is bloeddruk de kwantitatieve variabele en het type behandeling is de kwalitatieve..
We willen weten of de mediaan, en niet het gemiddelde, van de gemeten waarden statistisch gelijk of verschillend is, om vast te stellen of er een verschil is tussen de twee behandelingen. Om het antwoord te krijgen, wordt de Wilcoxon-statistiek of Mann-Whitney U-test toegepast..
Artikel index
- 1 Verklaring van het probleem in de Mann-Whitney U-test
- 1.1 Kwalitatieve variabelen versus kwantitatieve variabelen
- 2 Kenmerken van de Mann Whitney U-test
- 2.1 Mann-Whitney-formule
- 2.2 Stappen om de test toe te passen
- 3 Praktisch toepassingsvoorbeeld
- 3.1 - Stap 1
- 3.2 - Stap 2
- 3.3 Stap 3
- 3.4 Stap 4
- 4 online rekenmachines voor Mann's U-test - Whitney
- 5 referenties
Verklaring van het probleem in de Mann-Whitney U-test
Een ander voorbeeld waarin de test kan worden toegepast, is het volgende:
Stel dat u wilt weten of de consumptie van frisdrank significant verschilt in twee regio's van het land.
Een daarvan heet regio A en de andere regio B. Er wordt een record bijgehouden van de liters die wekelijks worden verbruikt in twee monsters: een van 10 personen voor regio A en een andere van 5 personen voor regio B.
De gegevens zijn als volgt:
-Regio A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12
-Regio B: 12,14, 11, 30, 10
De volgende vraag rijst:
Is de consumptie van frisdrank (Y) afhankelijk van de regio (X)?
Kwalitatieve variabelen versus kwantitatieve variabelen
-Kwalitatieve variabele X: Regio
-Kwantitatieve variabele Y: Frisdrankverbruik
Als de hoeveelheid verbruikte liters in beide regio's gelijk is, zal de conclusie zijn dat er geen afhankelijkheid is tussen de twee variabelen. De manier om erachter te komen, is door de gemiddelde of mediane trend voor de twee regio's te vergelijken.
Normaal geval
Als de gegevens een normale verdeling volgen, worden twee hypothesen opgeworpen: de nul H0 en de alternatieve H1 door de vergelijking tussen de gemiddelden:
-H0: er is geen verschil tussen het gemiddelde van de twee regio's.
-H1: de gemiddelden van beide regio's zijn verschillend.
Geval met niet-normale trend
Integendeel, als de gegevens geen normale verdeling volgen of als de steekproef gewoon te klein is om het te kennen, zou het in plaats van het gemiddelde te vergelijken, worden vergeleken de mediaan van de twee regio's.
-H0: er is geen verschil tussen de mediaan van de twee regio's.
-H1: de medianen van beide regio's zijn verschillend.
Als de medianen samenvallen, is de nulhypothese vervuld: er is geen verband tussen consumptie van frisdrank en de regio.
En als het tegenovergestelde gebeurt, is de alternatieve hypothese waar: er is een relatie tussen consumptie en regio.
In deze gevallen is de Mann-Whitney U-test aangewezen..
Gepaarde of ongepaarde monsters
De volgende belangrijke vraag bij het beslissen of de Mann Whitney U-test moet worden toegepast, is of het aantal gegevens in beide steekproeven identiek is, dat wil zeggen dat ze gelijk zijn..
Als de twee samples worden gecombineerd, is de originele Wilcoxon-versie van toepassing. Maar zo niet, zoals het geval is in het voorbeeld, dan wordt de gemodificeerde Wilcoxon-test toegepast, en dat is precies de Mann Whitney U-test..
Kenmerken van de Mann Whitney U-test
De Mann-Whitney U-test is een niet-parametrische test, toepasbaar op monsters die niet de normale verdeling volgen of met weinig gegevens. Het heeft de volgende kenmerken:
1. - Vergelijk de medianen
2.- Het werkt op bestelde reeksen
3.- Het is minder krachtig, aangezien het door macht wordt begrepen, de kans om de nulhypothese te verwerpen wanneer deze feitelijk onjuist is.
Rekening houdend met deze kenmerken, wordt de Mann-Whitney U-test toegepast wanneer:
-De gegevens zijn onafhankelijk
-Ze volgen niet de normale verdeling
-De nulhypothese H0 wordt geaccepteerd als de medianen van de twee steekproeven samenvallen: Ma = Mb
-De alternatieve hypothese H1 wordt geaccepteerd als de medianen van de twee steekproeven verschillen: Ma ≠ Mb
Mann-Whitney-formule
De variabele U is de contraststatistiek die wordt gebruikt in de Mann-Whitney-test en wordt als volgt gedefinieerd:
U = min (Ua, Ub)
Dit betekent dat U de kleinste waarde is tussen Ua en Ub, toegepast op elke groep. In ons voorbeeld zou het voor elke regio zijn: A of B.
De variabelen Ua en Ub worden gedefinieerd en berekend volgens de volgende formule:
Ua = Na Nb + Na (Na +1) / 2 - Ra
Ub = Na Nb + Nb (Nb +1) / 2 - Rb
Hier zijn de Na- en Nb-waarden de grootte van de monsters die overeenkomen met respectievelijk regio's A en B en van hun kant zijn Ra en Rb de rang bedragen die we hieronder zullen definiëren.
Stappen om de test toe te passen
1.- Bestel de waarden van de twee monsters.
2. - Wijs aan elke waarde een orderpositie toe.
3.- Corrigeer de bestaande ligaturen in de gegevens (herhaalde waarden).
4.- Bereken Ra = som van de bereiken van monster A.
5. - Vind Rb = Som van de rangen van monster B.
6.- Bepaal de waarde Ua en Ub volgens de formules in de vorige paragraaf.
7. - Vergelijk Ua en Ub, en de kleinste van de twee wordt toegewezen aan de experimentele U-statistiek (dat wil zeggen, van de gegevens) die wordt vergeleken met de theoretische of normale U-statistiek.
Praktisch toepassingsvoorbeeld
Nu passen we het bovenstaande toe op het probleem van eerder aan de orde gestelde frisdranken:
Regio A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12
Regio B: 12,14, 11, 30, 10
Afhankelijk van het feit of de gemiddelden van beide steekproeven statistisch hetzelfde of verschillend zijn, wordt de nulhypothese aanvaard of verworpen: er is geen verband tussen de variabelen Y en X, dat wil zeggen dat de consumptie van frisdrank niet afhankelijk is van de regio:
H0: Ma = Mb
H1: Ma ≠ Mb
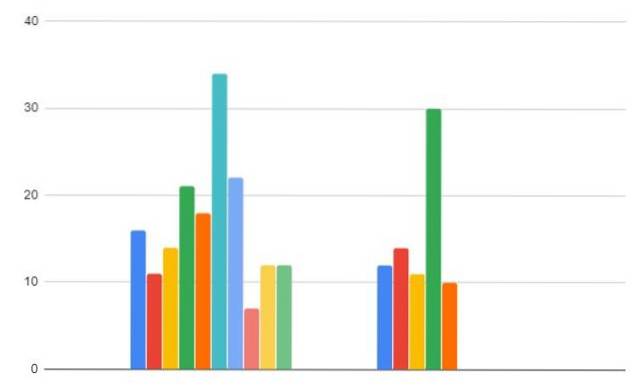
- Stap 1
We gaan verder met het gezamenlijk ordenen van de gegevens voor de twee monsters, waarbij we de waarden rangschikken van laag naar hoog:

Merk op dat de waarde 11 2 keer voorkomt (eenmaal in elk monster). Oorspronkelijk heeft het posities of bereiken 3 en 4, maar om de een of de ander niet te overschatten of te onderschatten, wordt de gemiddelde waarde gekozen als het bereik, dat wil zeggen 3,5.
Evenzo gaan we verder met de waarde 12, die drie keer wordt herhaald met bereiken 5, 6 en 7.
Welnu, de waarde 12 krijgt het gemiddelde bereik van 6 = (5 + 6 + 7) / 3 toegewezen. En hetzelfde voor de waarde 14, die ligatuur heeft (verschijnt in beide monsters) op posities 8 en 9, het krijgt het gemiddelde bereik 8,5 = (8 + 9) / 2 toegewezen.
- Stap 2
Vervolgens worden de gegevens voor regio A en B weer gescheiden, maar nu worden hun overeenkomstige bereiken in een andere rij aan hen toegewezen:
Regio A

Regio B

De bereiken Ra en Rb worden verkregen uit de sommen van de elementen van de tweede rij voor elk geval of gebied.
Stap 3
De respectievelijke Ua- en Ub-waarden worden berekend:
Ua = 10 × 5 + 10 (10 + 1) / 2 - 86 = 19
Ub = 10 × 5 + 5 (5 + 1) / 2-34 = 31
Experimentele waarde U = min (19, 31) = 19
Stap 4
Aangenomen wordt dat de theoretische U een normale verdeling N volgt met parameters die uitsluitend worden bepaald door de grootte van de monsters:
N ((na⋅nb) / 2, √ [na nb (na + nb +1) / 12])
Om de experimenteel verkregen variabele U te vergelijken met de theoretische U is het nodig om de variabele te veranderen. We gaan van de experimentele variabele U over naar zijn waarde getypeerd, die zal worden gebeld Z, om de vergelijking te kunnen maken met die van een gestandaardiseerde normale verdeling.
De verandering van variabele is als volgt:
Z = (U - na.nb / 2) / √ [na. nb (na + nb + 1) / 12]
Opgemerkt moet worden dat voor de verandering van variabele de parameters van de theoretische verdeling voor U werden gebruikt. Vervolgens wordt de nieuwe variabele Z, die een hybride is tussen de theoretische U en de experimentele U, gecontrasteerd met een gestandaardiseerde normale verdeling N (0 , 1).
Vergelijkingscriteria
Als Z ≤ Zα ⇒ de nulhypothese H0 wordt geaccepteerd
Als Z> Zα ⇒ nulhypothese H0 wordt verworpen
De gestandaardiseerde kritische Zα-waarden zijn afhankelijk van het vereiste betrouwbaarheidsniveau, bijvoorbeeld voor een betrouwbaarheidsniveau α = 0,95 = 95%, wat het meest gebruikelijk is, de kritische waarde Zα = 1,96.
Voor de gegevens die hier worden weergegeven:
Z = (U - na nb / 2) / √ [na nb (na + nb + 1) / 12] = -0,73
Dat is onder de kritische waarde 1,96.
De uiteindelijke conclusie is dus dat de nulhypothese H0 wordt geaccepteerd:
Er is geen verschil in de consumptie van frisdrank tussen regio A en B.
Online rekenmachines voor de Mann-Whitney U-test
Er zijn specifieke programma's voor statistische berekeningen, waaronder SPSS en MINITAB, maar deze programma's worden betaald en het gebruik ervan is niet altijd gemakkelijk. Dit komt door het feit dat ze zoveel opties bieden, dat het gebruik ervan praktisch is voorbehouden aan experts in de statistiek..
Gelukkig zijn er verschillende zeer nauwkeurige, gratis en gebruiksvriendelijke online programma's waarmee u onder andere de Mann-Whitney U-test kunt uitvoeren..
Deze programma's zijn:
-Social Science Statistics (socscistatistics.com), die zowel de Mann-Whitney U-test als de Wilcoxon-test heeft voor het geval van gebalanceerde of gepaarde monsters.
-AI Therapy Statistics (ai-therapy.com), die verschillende van de gebruikelijke tests van beschrijvende statistieken heeft.
-Te gebruiken statistiek (physics.csbsju.edu/stats), een van de oudste, dus de interface ziet er misschien gedateerd uit, hoewel het niettemin een zeer efficiënt gratis programma is.
Referenties
- Dietrichson. Kwantitatieve methoden: rangschikkingstest. Hersteld van: bookdown.org
- Marín J P. SPSS-gids: analyse en procedures in niet-parametrische tests. Hersteld van: halweb.uc3m.es
- USAL MOOC. Niet-parametrische tests: Mann - Whitney U. Hersteld van: youtube.com
- Wikipedia. Mann-Whitney U-test. Hersteld van: es.wikipedia.com
- XLSTAT. Helpcentrum. Mann - Whitney-testhandleiding in Excel. Hersteld van: help.xlsat.com


Niemand heeft nog op dit artikel gereageerd.