
Wat is een deterministisch experiment?
De deterministisch experiment, in de statistieken is het een resultaat dat een voorspelbaar en reproduceerbaar resultaat heeft, zolang dezelfde initiële voorwaarden en parameters worden gehandhaafd. Dat wil zeggen, de oorzaak-gevolgrelatie is volledig bekend.
De tijd die het zand van een klok nodig heeft om van het ene compartiment naar het andere te gaan, is bijvoorbeeld een deterministisch experiment, omdat het resultaat voorspelbaar en reproduceerbaar is. Zolang de omstandigheden hetzelfde zijn, duurt het even lang om van capsule naar capsule te reizen.

Veel fysische verschijnselen zijn deterministisch, enkele voorbeelden zijn de volgende:
- Een object dat dichter is dan water, zoals een steen, zal altijd zinken.
- Een vlotter, die minder dicht is dan water, zal altijd omhoog drijven (tenzij een kracht wordt uitgeoefend om hem onder water te houden).
- De kooktemperatuur van water op zeeniveau is altijd 100 ºC.
- De tijd die nodig is voor een dobbelsteen die van rust valt, omdat deze wordt bepaald door de hoogte vanwaar hij viel en deze tijd is altijd hetzelfde (wanneer hij van dezelfde hoogte valt).
Profiteren van het voorbeeld van de dobbelstenen. Als het valt, zelfs als ervoor wordt gezorgd dat het dezelfde oriëntatie en altijd op dezelfde hoogte heeft, is het moeilijk te voorspellen aan welke kant het zal verschijnen als het eenmaal op de grond is gestopt. Dit zou een willekeurig experiment zijn.
Theoretisch, als gegevens zoals: positie met oneindige precisie bekend waren; beginsnelheid en oriëntatie van de matrijs; vorm (met afgeronde of hoekige randen); en de restitutiecoëfficiënt van het oppervlak waarop het valt, zou het misschien mogelijk zijn om door complexe berekeningen te voorspellen welke kant de dobbelsteen zal verschijnen wanneer het stopt. Maar elke kleine variatie in de startcondities zou een ander resultaat opleveren..
Dergelijke systemen zijn deterministisch en tegelijkertijd chaotisch, aangezien een kleine wijziging van de beginvoorwaarden het eindresultaat op een willekeurige manier verandert..
Artikel index
- 1 Meting
- 1.1 Variaties in meting
- 2 Resultaten van een meting en fout
- 2.1 - Meetfout
- 2.2 - Berekening van de meetfout
- 3 referenties
Meting
Deterministische experimenten zijn volledig meetbaar, maar toch is de meting van hun resultaat niet oneindig nauwkeurig en heeft een zekere onzekerheidsmarge.
Neem bijvoorbeeld het volgende volstrekt deterministische experiment: een speelgoedauto laten vallen op een hellende rechte baan.

Het wordt altijd vanuit hetzelfde startpunt losgelaten, waarbij je erop moet letten geen enkele impuls te geven. In dit geval moet de tijd die de auto nodig heeft om over de baan te rijden altijd dezelfde zijn.
Nu gaat een kind op zoek naar de tijd die het karretje nodig heeft om over de baan te rijden. Hiervoor gebruikt u de stopwatch die in uw mobiele telefoon is ingebouwd.
Als oplettende jongen valt het eerste op dat je meetinstrument een eindige precisie heeft, want het kleinste tijdsverschil dat de stopwatch kan meten is 1 honderdste van een seconde..
Vervolgens gaat het kind verder met het uitvoeren van het experiment en meet met de mobiele stopwatch 11 keer - laten we zeggen voor de zekerheid - de tijd die de wandelwagen nodig had om het hellende vlak af te leggen, waarbij de volgende resultaten worden verkregen:
3.12s 3.09s 3.04s 3.04s 3.10s 3.08s 3.05s 3.10s 3.11s 3.06s en 3.03s.
Het kind is verrast, want op school hadden ze hem verteld dat dit een deterministisch experiment is, maar bij elke meting kreeg hij een iets ander resultaat.
Variaties in maatvoering
Wat kunnen de oorzaken zijn dat elke meting een ander resultaat heeft??
Een mogelijke oorzaak kan de precisie van het instrument zijn, die, zoals eerder vermeld, 0,01 s is. Maar houd er rekening mee dat de verschillen in de metingen boven die waarde liggen, dus andere oorzaken moeten worden overwogen, zoals:
- Kleine variaties vanaf het startpunt.
- Verschillen in het starten en pauzeren van de stopwatch, vanwege de reactietijd van het kind.
Wat betreft de reactietijd is er zeker een vertraging vanaf het moment dat het kind ziet dat het karretje gaat rijden, totdat het op de stopwatch drukt..
Evenzo is er bij aankomst een vertraging vanwege de reactietijd. Maar de start- en aankomstvertragingen worden gecompenseerd, dus de verkregen tijd moet heel dicht bij de werkelijke tijd liggen..
In ieder geval is de compensatie voor de reactievertraging niet exact, omdat de reactietijden in elke test kleine variaties kunnen hebben, wat de verschillen in de resultaten verklaart..
Wat is dan het echte resultaat van het experiment??
Resultaten van een meting en fout
Om het uiteindelijke resultaat te rapporteren, moeten we statistieken gebruiken. Laten we eerst kijken hoe vaak de resultaten worden herhaald:
- 3.03s (1 keer)
- 3.04s (2 keer)
- 3.05s (1 keer)
- 3.06s (1 keer)
- 3.08s (1 keer)
- 3.09s 1 keer
- 3.10s (2 keer)
- 3.11s (1 keer)
- 3.12s (1 keer)
Bij het bestellen van de data realiseren we ons dat a mode of meer herhaald resultaat. Het te rapporteren resultaat is dan het rekenkundig gemiddelde, dat als volgt kan worden berekend:
(1 × 3.03 + 2 × 3.04 + 1 × 3.05 + 1x 3.06 + 1 × 3.08 + 1 × 3.09 + 2 × 3.10 + 1 × 3.11 + 1 × 3.12) / (1 + 2 + 1 + 1 + 1 + 1 + 2 + 1 + 1).
Het resultaat van de bovenstaande berekening is 3.074545455. Logischerwijs heeft het geen zin om al deze decimalen in het resultaat te vermelden, omdat elke meting slechts 2 decimalen nauwkeurig heeft..
Door de afrondingsregels toe te passen, kan worden gesteld dat de tijd die het karretje nodig heeft om over de baan te rijden, het rekenkundig gemiddelde is, afgerond op twee decimalen..
Het resultaat dat we kunnen rapporteren voor ons experiment is:
3,08 seconden is de tijd die de speelgoedauto nodig heeft om de hellingbaan af te leggen.
- Meetfout
Zoals we hebben gezien in ons voorbeeld van een deterministisch experiment, heeft elke meting een fout, omdat deze niet met oneindige precisie kan worden gemeten..
Het enige dat in ieder geval kan worden gedaan, is het verbeteren van de instrumenten en de meetmethoden om een nauwkeuriger resultaat te verkrijgen..
In de vorige paragraaf gaven we een resultaat van ons deterministische experiment van de tijd die de speelgoedauto nodig heeft om een hellend spoor af te leggen. Maar dit resultaat bevat een fout. Nu zullen we uitleggen hoe we die fout kunnen berekenen.
- Berekening van de meetfout
In de metingen voor tijd wordt een spreiding genoteerd in de uitgevoerde metingen. De standaardafwijking is een formulier dat vaak in statistieken wordt gebruikt om de verspreiding van gegevens te rapporteren.
Variantie en standaarddeviatie
De manier om de standaarddeviatie te berekenen is als volgt: eerst zoek je de variantie van de gegevens, op deze manier gedefinieerd:
De som van de verschillen van elk resultaat met het rekenkundig gemiddelde, in het kwadraat en gedeeld door het totale aantal gegevens
Als de variantie de vierkantswortel wordt genomen, wordt de standaarddeviatie verkregen.
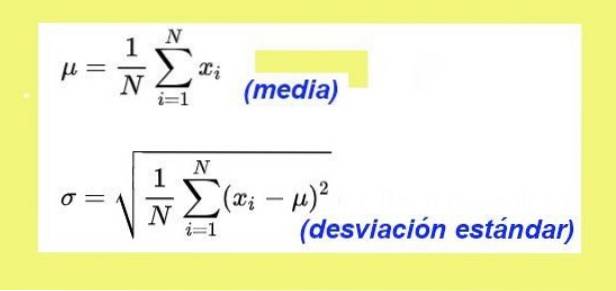
De standaarddeviatie voor de gegevens over de afdalingstijd van de speelgoedauto is:
σ = 0,03
Het resultaat is afgerond op 2 decimalen, omdat de nauwkeurigheid van elk van de gegevens 2 decimalen is. In dit geval vertegenwoordigt 0,03 s de statistische fout van elk van de gegevens..
Het gemiddelde of rekenkundig gemiddelde van de verkregen tijden heeft echter een kleinere fout. De gemiddelde fout wordt berekend door de standaarddeviatie te delen door de vierkantswortel van het totale aantal gegevens..
Gemiddelde fout = σ / √N = 0,03 / √11 = 0,01
Dat wil zeggen, de statistische fout van het tijdsgemiddelde is 1 honderdste van een seconde en valt in dit voorbeeld samen met de waardering van de stopwatch, maar dit is niet altijd het geval..
Als eindresultaat van de meting wordt dan gerapporteerd:
t = 3,08 s ± 0,01 s is de tijd die de speelgoedauto nodig heeft om de hellende baan af te leggen.
Geconcludeerd wordt dat zelfs als het een deterministisch experiment is, het resultaat van de meting niet oneindig nauwkeurig is en altijd een foutmarge heeft..
En ook, om het eindresultaat te rapporteren, is het noodzakelijk om, zelfs als het een deterministisch experiment is, statistische methoden te gebruiken.
Referenties
- CanalPhi. Deterministisch experiment. Hersteld van: youtube.com
- MateMovil. Deterministisch experiment. Hersteld van: youtube.com
- Pishro Nick H. Inleiding tot waarschijnlijkheid. Hersteld van: probabilitycourse.com
- Ross. Waarschijnlijkheid en statistieken voor ingenieurs. Mc-Graw Hill.
- Statistiek hoe. Deterministisch: definitie en voorbeelden. Hersteld van: statisticshowto.datasciencecentral.com
- Wikipedia. Typische afwijking. Hersteld van: es.wikipedia.com
- Wikipedia. Experiment (kansrekening). Hersteld van: en.wikipedia.com


Niemand heeft nog op dit artikel gereageerd.