
Wat is een icosagon? Kenmerken en eigenschappen

EEN icosagon of isodecagon is een veelhoek met 20 zijden. Een veelhoek is een vlakke figuur gevormd door een eindige reeks lijnsegmenten (meer dan twee) die een gebied van het vlak omsluiten.
Elk lijnsegment wordt een zijde genoemd en het snijpunt van elk paar zijden wordt een hoekpunt genoemd. Afhankelijk van het aantal zijden krijgen de polygonen een bepaalde naam.

De meest voorkomende zijn de driehoek, vierhoek, vijfhoek en zeshoek, die respectievelijk 3, 4, 5 en 6 zijden hebben, maar kunnen worden gebouwd met het aantal zijden dat u wilt.
Kenmerken van een icosagon
Hieronder staan enkele kenmerken van polygonen en hun toepassing in een icosagon.
1- Classificatie
Een icosagon, die een veelhoek is, kan worden geclassificeerd als regelmatig en onregelmatig, waarbij het woord regelmatig verwijst naar het feit dat alle zijden dezelfde lengte hebben en de binnenhoeken allemaal hetzelfde meten; anders wordt er gezegd dat de icosagon (polygoon) onregelmatig is.
2- Isodecagon
De reguliere icosagon wordt ook wel een reguliere isodecagon genoemd, want om een reguliere icosagon te krijgen, moet je elke zijde van een regelmatige decagon (10-zijdige veelhoek) halveren (in twee gelijke delen verdelen)..
3- Omtrek
Om de omtrek "P" van een regelmatige veelhoek te berekenen, wordt het aantal zijden vermenigvuldigd met de lengte van elke zijde.
In het specifieke geval van een icosagon is de omtrek gelijk aan 20xL, waarbij 'L' de lengte van elke zijde is.
Als u bijvoorbeeld een gewone icosagon heeft met een zijde van 3 cm, is de omtrek gelijk aan 20x3 cm = 60 cm.
Het is duidelijk dat, als de isogon onregelmatig is, de bovenstaande formule niet kan worden toegepast.
In dit geval moeten de 20 zijden afzonderlijk worden opgeteld om de omtrek te verkrijgen, d.w.z. de omtrek "P" is gelijk aan ∑Li, met i = 1,2, ..., 20.
4- Diagonalen
Het aantal diagonalen "D" dat een polygoon heeft, is gelijk aan n (n-3) / 2, waarbij n staat voor het aantal zijden.
In het geval van een icosagon volgt hieruit dat deze D = 20x (17) / 2 = 170 diagonalen heeft.
5- Som van de interne hoeken
Er is een formule die helpt bij het berekenen van de som van de interne hoeken van een regelmatige veelhoek, die kan worden toegepast op een regelmatige icosagon.
De formule bestaat uit het aftrekken van 2 van het aantal zijden van de polygoon en dit getal vervolgens te vermenigvuldigen met 180º.
De manier waarop deze formule wordt verkregen, is dat we een polygoon met n zijden kunnen verdelen in n-2 driehoeken, en gebruikmakend van het feit dat de som van de interne hoeken van een driehoek 180º is, krijgen we de formule.
De volgende afbeelding illustreert de formule voor een regelmatige enegon (9-zijdige veelhoek).
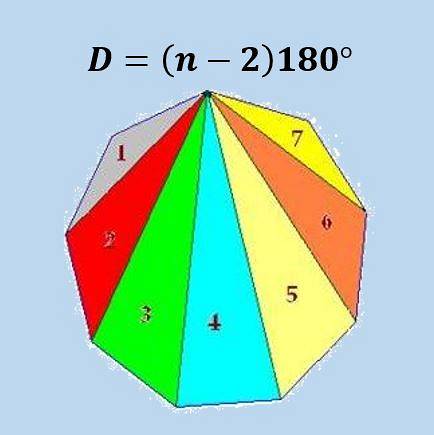
Met behulp van de bovenstaande formule wordt verkregen dat de som van de interne hoeken van een icosagon 18 × 180º = 3240º of 18π is.
6- Gebied
Om de oppervlakte van een regelmatige veelhoek te berekenen, is het erg handig om het concept apothema te kennen. De apothema is een loodrechte lijn die loopt van het midden van de regelmatige veelhoek naar het middelpunt van een van zijn zijden.
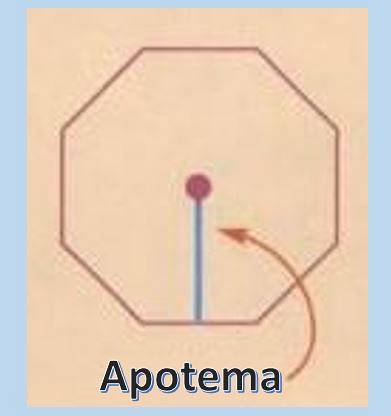
Als de lengte van de apothema eenmaal bekend is, is de oppervlakte van een regelmatige veelhoek A = Pxa / 2, waarbij "P" de omtrek voorstelt en "a" de apothema..
In het geval van een gewone icosagon is het gebied A = 20xLxa / 2 = 10xLxa, waarbij 'L' de lengte van elke zijde is en 'a' de apothema.
Aan de andere kant, als je een onregelmatige veelhoek hebt met n zijden, om zijn oppervlakte te berekenen, deel je de veelhoek in n-2 bekende driehoeken, bereken dan de oppervlakte van elk van deze n-2 driehoeken en tel tenslotte al deze gebieden op.
De hierboven beschreven methode staat bekend als triangulatie van een veelhoek.
Referenties
- C., E. Á. (2003). Geometrische elementen: met talrijke oefeningen en kompasgeometrie. Universiteit van Medellin.
- Campos, F. J., Cerecedo, F. J., & Cerecedo, F. J. (2014). Wiskunde 2. Grupo Redactie Patria.
- Freed, K. (2007). Ontdek Polygonen. Benchmark Onderwijsbedrijf.
- Hendrik, v. M. (2013). Gegeneraliseerde polygonen. Birkhäuser.
- IGER. (s.f.). Wiskunde eerste semester Tacaná. IGER.
- jrgeometry. (2014). Veelhoeken. Lulu Press, Inc.
- Mathivet, V. (2017). Kunstmatige intelligentie voor ontwikkelaars: concepten en implementatie in Java. ENI-edities.
- Miller, Heeren en Hornsby. (2006). Wiskunde: redenering en toepassingen 10 / e (Tiende editie red.). Pearson Education.
- Oroz, R. (1999). Woordenboek van de Spaanse taal. University Publishing House.
- Patiño, M. d. (2006). Wiskunde 5. Redactioneel Progreso.
- Rubió, M. d.-M. (1997). De vormen van stedelijke groei. Univ. Politèc. uit Catalunya.



Niemand heeft nog op dit artikel gereageerd.