
Exponentiële afvlakkingsmethode en voorbeeld
De exponentiële afvlakking het is een manier om de vraag naar een item voor een bepaalde periode te voorspellen. Deze methode schat dat de vraag gelijk zal zijn aan het gemiddelde van het historische verbruik in een bepaalde periode, waardoor een groter gewicht of gewicht wordt toegekend aan de waarden die dichter in de tijd liggen. Houd bovendien bij de volgende prognoses rekening met de bestaande fout van de huidige prognose.
Vraagvoorspelling is de methode om de vraag van de klant naar een product of dienst te projecteren. Dit proces is continu, waarbij managers historische gegevens gebruiken om te berekenen wat ze verwachten dat de verkoopvraag naar een goed of dienst zal zijn..
Informatie uit het verleden van het bedrijf wordt gebruikt door deze toe te voegen aan de economische gegevens van de markt om te zien of de verkoop zal stijgen of dalen.
De resultaten van de vraagprognose worden gebruikt om doelen te stellen voor de verkoopafdeling, waarbij wordt geprobeerd in lijn te blijven met de doelen van het bedrijf.
Artikel index
- 1 Exponentiële afvlakkingsmethode
- 1.1 Smoothing in de prognose
- 1.2 Gewogen voortschrijdend gemiddelde
- 1.3 Exponentiële afvlakking
- 2 Voorbeeld
- 3 referenties
Exponentiële afvlakkingsmethode
Afvlakken is een heel gebruikelijk statistisch proces. Afgevlakte gegevens worden vaak aangetroffen in verschillende vormen van het dagelijks leven. Elke keer dat een gemiddelde wordt gebruikt om iets te beschrijven, wordt een afgevlakt getal gebruikt.
Stel dat de warmste winter ooit werd meegemaakt dit jaar. Om het te kwantificeren, beginnen we met de set van dagelijkse temperatuurgegevens voor de winterperiode van elk geregistreerd historisch jaar..
Dit genereert een aantal getallen met grote “sprongen”. Je hebt een getal nodig dat al deze sprongen uit de gegevens verwijdert om de ene winter gemakkelijker met de andere te kunnen vergelijken.
Het elimineren van de sprong in de gegevens wordt afvlakken genoemd. In dit geval kan een eenvoudig gemiddelde worden gebruikt om afvlakking te bereiken.
Afvlakken van de prognose
Voor het voorspellen van de vraag wordt afvlakking ook gebruikt om variaties in de historische vraag te elimineren. Hierdoor kunnen vraagpatronen beter worden geïdentificeerd, die kunnen worden gebruikt om de toekomstige vraag in te schatten..
Variaties in de vraag is hetzelfde concept als de "sprong" van temperatuurgegevens. De meest gebruikelijke manier waarop variaties in de vraaghistorie worden verwijderd, is door gebruik te maken van een gemiddelde of specifiek een voortschrijdend gemiddelde..
Het voortschrijdend gemiddelde gebruikt een vooraf gedefinieerd aantal perioden om het gemiddelde te berekenen, en die perioden verplaatsen zich naarmate de tijd verstrijkt..
Als bijvoorbeeld een voortschrijdend gemiddelde over vier maanden wordt gebruikt en het vandaag 1 mei is, wordt de gemiddelde vraag voor januari, februari, maart en april gebruikt. Op 1 juni wordt de vraag voor februari, maart, april en mei benut.
Gewogen voortschrijdend gemiddelde
Bij gebruik van een eenvoudig gemiddelde wordt hetzelfde belang toegepast op elke waarde in de dataset. Daarom vertegenwoordigt bij een voortschrijdend gemiddelde van vier maanden elke maand 25% van het voortschrijdend gemiddelde..
Door vraaghistorie te gebruiken om toekomstige vraag te projecteren, is het logisch dat de meest recente periode een grotere impact heeft op de prognose..
U kunt de berekening van het voortschrijdend gemiddelde aanpassen om verschillende "gewichten" toe te passen op elke periode om de gewenste resultaten te verkrijgen..
Deze gewichten worden uitgedrukt in percentages. Het totaal van alle gewichten voor alle perioden moet oplopen tot 100%.
Als u daarom 35% wilt toepassen als het gewicht voor de dichtstbijzijnde periode in het gewogen gemiddelde van vier maanden, kunt u 35% aftrekken van 100%, zodat 65% overblijft om te verdelen over de drie resterende perioden.
U kunt bijvoorbeeld eindigen met een weging van respectievelijk 15%, 20%, 30% en 35% voor de vier maanden (15 + 20 + 30 + 35 = 100).
Exponentiële afvlakking
De stuuringang voor de exponentiële afvlakkingsberekening staat bekend als de afvlakfactor. Geeft het gewicht weer dat is toegepast op de vraag voor de meest recente periode.
Als 35% wordt gebruikt als het meest recente periodegewicht in de berekening van het gewogen voortschrijdend gemiddelde, kunt u er ook voor kiezen om 35% te gebruiken als de afvlakkingsfactor in de exponentiële afvlakkingsberekening..
Exponentieel deel
Het verschil in de berekening van de exponentiële afvlakking is dat in plaats van te moeten uitzoeken hoeveel gewicht op elke voorgaande periode moet worden toegepast, de afvlakkingsfactor wordt gebruikt om dat automatisch te doen..
Dit is het "exponentiële" deel. Als 35% als afvlakkingsfactor wordt gehanteerd, is het vraaggewicht voor de meest recente periode 35%. De weging van de vraag uit de vorige periode naar de meest recente is 65% van 35%.
65% komt van 35% aftrekken van 100%. Dit komt overeen met een weging van 22,75% voor die periode. De volgende meest recente periodevraag is 65% van 65% van 35%, wat gelijk is aan 14,79%.
De vorige periode wordt gewogen als 65% van 65% van 65% van 35%, wat overeenkomt met 9,61%. Dit gebeurt voor alle voorgaande periodes, tot en met de eerste periode.
Formule
De formule voor het berekenen van exponentiële afvlakking is als volgt: (D * S) + (P * (1-S)), waarbij,
D = meest recente vraag van de periode.
S = afvlakkingsfactor, weergegeven in decimale vorm (35% zou 0,35 zijn).
P = prognose van de meest recente periode, resultaat van de afvlakkingsberekening van de vorige periode.
Ervan uitgaande dat we een afvlakkingsfactor van 0,35 hebben, zouden we dan hebben: (D * 0,35) + (P * 0,65).
Zoals u kunt zien, zijn de enige vereiste gegevensinvoer de vraag en de meest recente periodeprognose..
Voorbeeld
Een verzekeringsmaatschappij heeft besloten om zijn markt uit te breiden naar de grootste stad van het land en biedt autoverzekeringen aan.
Als eerste actie wil het bedrijf voorspellen hoeveel autoverzekeringen de inwoners van deze stad zullen afsluiten.
Om dit te doen, gebruiken ze als eerste gegevens het bedrag van de autoverzekering die in een andere kleinere stad is gekocht.
De vraagprognose voor periode 1 is 2.869 gecontracteerde autoverzekeringen, maar de werkelijke vraag in die periode was 3.200.
Naar goeddunken van het bedrijf kent het een afvlakkingsfactor van 0,35 toe. De verwachte vraag voor de volgende periode is: P2 = (3200 * 0,35) + 2869 * (1-0,35) = 2984,85.
Dezelfde berekening werd gemaakt voor het hele jaar, waarbij de volgende vergelijkingstabel werd verkregen tussen wat feitelijk werd verkregen en wat werd voorspeld voor die maand.
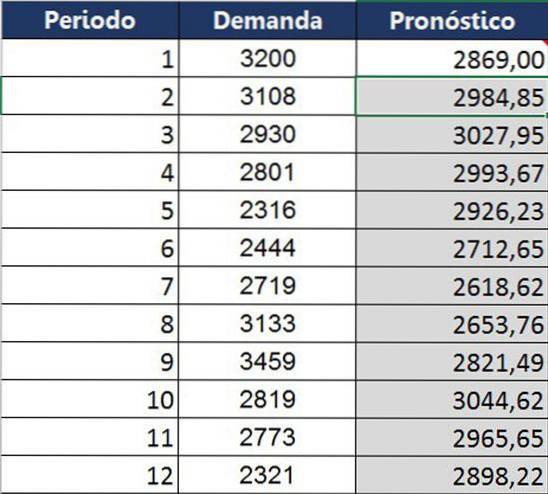
In vergelijking met middelingstechnieken kan exponentiële afvlakking de trend beter voorspellen. Het schiet echter nog steeds tekort, zoals te zien is in de grafiek:
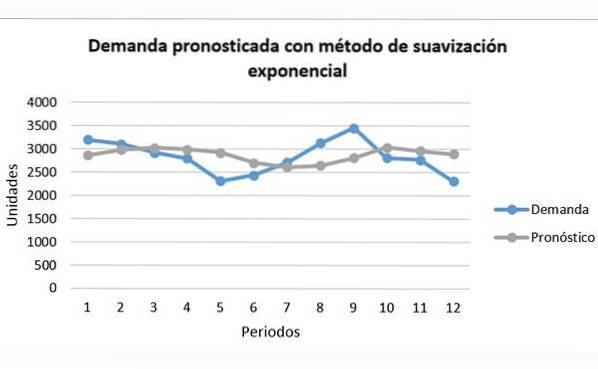
Het is te zien hoe de grijze lijn van de prognose ver onder of boven de blauwe lijn van de vraag kan zijn, zonder deze volledig te kunnen volgen.
Referenties
- Wikipedia (2019). Exponentiële afvlakking. Ontleend aan: es.wikipedia.org.
- Ingenio Empresa (2016). Hoe u eenvoudige exponentiële afvlakking gebruikt om de vraag te voorspellen. Overgenomen van: ingenioempresa.com.
- Dave Piasecki (2019). Exponentiële afvlakking uitgelegd. Genomen uit: inventoryops.com.
- Onderzoek (2019). Technieken voor vraagvoorspelling: voortschrijdend gemiddelde en exponentiële afvlakking. Genomen van: study.com.
- Cityu (2019). Exponentiële afvlakkingsmethoden. Genomen uit: personal.cb.cityu.edu.hk.



Niemand heeft nog op dit artikel gereageerd.