
Derde wet van thermodynamische formules, vergelijkingen, voorbeelden
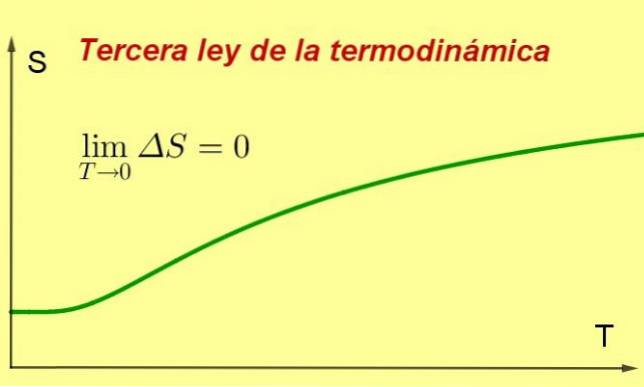
De Derde wet van de thermodynamica stelt dat de entropie van een gesloten thermodynamisch systeem in evenwicht meestal minimaal en constant is, aangezien de temperatuur 0 kelvin nadert.
Deze entropiewaarde is onafhankelijk van de systeemvariabelen (onder andere druk of aangelegd magnetisch veld). Wat er gebeurt, is dat naarmate de temperatuur dichter bij 0 K komt, de processen in het systeem stoppen en omdat entropie een maat is voor interne agitatie, deze noodzakelijkerwijs daalt.
Artikel index
- 1 Eerdere concepten
- 1.1 Thermodynamisch systeem
- 1.2 Geïsoleerde, gesloten of open systemen
- 1.3 Macrostaten en microstaten
- 2 Formules en vergelijkingen
- 2.1 Berekening van de absolute entropie van een stof
- 3 Toepassingen
- 3.1 Entropie van een systeem bij lage temperatuur
- 3.2 Resterende entropie
- 4 voorbeelden
- 4.1 Voorbeeld 1: het absolute nulpunt en de onbepaaldheid van Heisenberg
- 4.2 Voorbeeld 2: Superfluïditeit en het vreemde geval van helium-4
- 5 oefeningen opgelost
- 5.1 - Oefening 1
- 5.2 - Oefening 2
- 6 referenties
Eerdere concepten
Om de reikwijdte van de derde wet van de thermodynamica te begrijpen, relevant bij zeer lage temperaturen, is het noodzakelijk om de volgende concepten te herzien:
Thermodynamisch systeem
Over het algemeen verwijst naar een gas, een vloeistof of een vaste stof. Wat geen deel uitmaakt van het systeem wordt genoemd milieu. Het meest voorkomende thermodynamische systeem is het ideale gas, dat bestaat uit N-deeltjes (atomen) die alleen op elkaar inwerken door elastische botsingen.
Geïsoleerde, gesloten of open systemen
Geïsoleerde systemen mogen niet uitgewisseld worden met de omgeving. Gesloten systemen wisselen geen materie uit met de omgeving, maar wel warmte. Ten slotte kunnen open systemen zowel materie als warmte uitwisselen met de omgeving..
Macrostaten en microstaten
De macrostaat van een systeem is de reeks waarden die de variabelen hebben: druk, temperatuur, volume, aantal mol, entropie en interne energie. Aan de andere kant wordt de microstaat -in het geval van een ideaal gas- gegeven door de positie en het momentum van elk van de N-deeltjes waaruit het bestaat, op een bepaald moment.
Veel microstaten kunnen resulteren in dezelfde macrostaat. In een gas op kamertemperatuur is het aantal mogelijke microstaten enorm, omdat het aantal deeltjes waaruit het bestaat, de verschillende posities en de verschillende energieën die ze kunnen aannemen erg groot is..
Formules en vergelijkingen
Entropie, zoals we al zeiden, is een thermodynamische macroscopische variabele die de mate van moleculaire wanorde van het systeem meet. De mate van wanorde van een systeem is groter naarmate het aantal mogelijke microstates groter is.
Dit concept is nodig om de derde wet van de thermodynamica in wiskundige vorm te formuleren. Laat S de entropie van het systeem zijn, dan:

Entropie is een macroscopische toestandsvariabele die rechtstreeks verband houdt met het aantal mogelijke microstaten van een systeem, door middel van de volgende formule:
S = k ln (W)
In de bovenstaande vergelijking: S vertegenwoordigt entropie, W. het aantal mogelijke microstates van het systeem en k is de constante van Boltzmann (k = 1,38 x 10-2. 3 J / KDat wil zeggen, de entropie van een systeem is k maal de natuurlijke logaritme van het aantal mogelijke microstaten.
Berekening van de absolute entropie van een stof
Het is mogelijk om de absolute entropie van een zuivere stof te definiëren uitgaande van de definitie van de entropievariatie:

δQ = n. cp .dT
Hier is cp de molaire soortelijke warmte en n het aantal mol. De afhankelijkheid van molaire soortelijke warmte met temperatuur is een experimenteel verkregen data en bekend voor veel zuivere stoffen..
Volgens de derde wet over zuivere stoffen:


Toepassingen
In het dagelijks leven heeft de derde wet van de thermodynamica weinig toepassingen, precies het tegenovergestelde van de eerste en tweede wet. Het is omdat het een principe is dat verwijst naar wat er gebeurt in een systeem wanneer het de absolute 0 nadert, een zeldzaam temperatuurbereik.
In feite is het bereiken van absolute 0 of −273,15 ° C onmogelijk (zie voorbeeld 1 hieronder). De derde wet is echter van toepassing bij het bestuderen van de respons van materialen bij zeer lage temperaturen.
Hierdoor zijn er belangrijke vorderingen gemaakt in de fysica van gecondenseerde materie, zoals:
-Superfluïditeit (zie voorbeeld 2 hieronder)
-Supergeleiding
-Laserkoelingstechnieken
-Bose-Einstein-condensaat
-Fermi superfluïde gassen.

Bij extreem lage temperaturen zorgt de afname van entropie voor het ontstaan van interessante kwantumverschijnselen. Laten we daarom eens kijken wat er gebeurt met de entropie van een systeem bij zeer lage temperatuur.
Entropie van een systeem bij lage temperatuur
Als je een perfect kristallijne substantie hebt, is de minimale entropie ervan precies nul, omdat het een sterk geordend systeem is. Bij temperaturen dichtbij het absolute 0, bevindt materie zich in een gecondenseerde toestand (vloeibaar of vast) en zijn trillingen in het kristal minimaal.
Sommige auteurs beschouwen een alternatieve verklaring van de derde wet van de thermodynamica als het volgende:
"Als materie condenseert om een perfect kristal te vormen, neigt de entropie naar exact nul wanneer de temperatuur naar het absolute nulpunt neigt".
Laten we enkele aspecten van de vorige verklaring verduidelijken:
- Een perfect kristal is er een waarin elk molecuul identiek is en waarin de moleculaire structuur zich identiek in zijn geheel herhaalt..
- Naarmate de temperatuur het absolute nulpunt nadert, neemt de atoomtrilling bijna volledig af.
Dan vormt het kristal een enkele configuratie of mogelijke microstaat, dat wil zeggen, W = 1, en daarom is de entropie gelijk aan nul:
S = k ln (1) = 0
Maar het is niet altijd dat een materiaal dat afgekoeld is tot bijna het absolute nulpunt een kristal vormt, laat staan dat dit kristal perfect is. Dit gebeurt alleen als het afkoelingsproces erg traag en omkeerbaar is..
Anders zouden factoren zoals onzuiverheden die in het glas aanwezig zijn, het bestaan van andere microstaten mogelijk maken. Daarom zou W> 1 en de entropie groter zijn dan 0.
Resterende entropie
Als het afkoelingsproces abrupt is, doorloopt het systeem een opeenvolging van niet-evenwichtstoestanden, waardoor het materiaal verglaasd raakt. In dit geval ontstaat er geen geordende kristallijne structuur, maar een amorfe vaste stof, waarvan de structuur vergelijkbaar is met die van een vloeistof..
In dat geval is de minimale entropiewaarde in de buurt van het absolute nulpunt niet nul, aangezien het aantal microstaten aanzienlijk groter is dan 1. Het verschil tussen deze entropie en de nul entropie van de perfect kristallijne toestand staat bekend als de resterende entropie.
De verklaring is dat onder een bepaalde drempeltemperatuur het systeem geen andere keus heeft dan de microstaten te bezetten met lagere energie, die, omdat ze gekwantiseerd zijn, een vast getal vormen.
Zij zorgen ervoor dat de entropie constant blijft, ook als de temperatuur verder daalt richting het absolute nulpunt..
Voorbeelden
Voorbeeld 1: het absolute nulpunt en de onbepaaldheid van Heisenberg
Heisenbergs principe van onbepaaldheid stelt vast dat de onzekerheid in de positie en het momentum van een deeltje, bijvoorbeeld in de atomen van een kristalrooster, niet onafhankelijk van elkaar zijn, maar eerder de volgende ongelijkheid volgen:
Δx ⋅ Δp ≥ h
Waar h de constante van Planck is. Dat wil zeggen, de onzekerheid in positie vermenigvuldigd met de onzekerheid in momentum (massa maal snelheid) is groter dan of gelijk aan de constante van Planck, waarvan de waarde erg klein is, maar niet nul: h = 6,63 x 10-3. 4 J s.
En wat heeft het onzekerheidsprincipe te maken met de derde wet van de thermodynamica? Als de positie van de atomen in het kristalrooster vast en nauwkeurig is (Δx = 0) dan kan de snelheid van deze atomen elke waarde tussen 0 en oneindig aannemen. Dit wordt tegengesproken door het feit dat bij het absolute nulpunt alle beweging van thermische agitatie stopt..
Omgekeerd, als we aannemen dat bij het absolute nulpunt alle agitatie stopt en het momentum van elk atoom in het rooster precies nul is (Δp = 0), dan zou het Heisenberg-onzekerheidsprincipe impliceren dat de onbepaaldheid in de posities van elk atoom oneindig zou zijn, dat wil zeggen dat ze in elke positie kunnen zijn.
Als gevolg van de vorige verklaring zou het aantal microstates neigen tot oneindig en zou de entropie ook een onbepaalde waarde aannemen.
Voorbeeld 2: Superfluïditeit en het vreemde geval van helium-4
In superfluïditeit, dat optreedt bij zeer lage temperaturen, verliest materie de interne wrijving tussen zijn moleculen, genaamd viscositeit. In zo'n geval zou de vloeistof voor altijd zonder wrijving kunnen circuleren, maar het probleem is dat bij die temperaturen bijna niets vloeibaar is behalve helium..
Helium en helium 4 (de meest voorkomende isotoop) vormen een uniek geval, aangezien helium bij atmosferische druk en temperaturen dichtbij het absolute nulpunt vloeibaar blijft.
Wanneer helium-4 wordt blootgesteld aan een temperatuur lager dan 2,2 K bij atmosferische druk, wordt het a superfluïde. Deze ontdekking vond plaats in 1911 in Leiden door de Nederlandse natuurkundige Heike Kamerlingh Onnes (1853-1926).
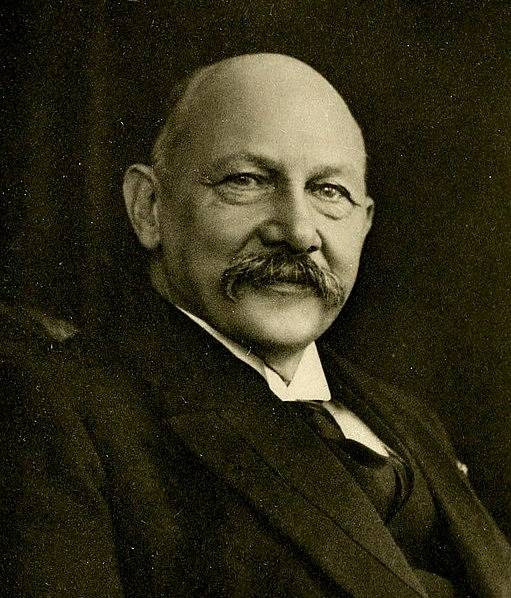
Het helium-4-atoom is een boson. Bosonen zijn, in tegenstelling tot fermionen, deeltjes die allemaal dezelfde kwantumtoestand kunnen innemen. Bosonen voldoen daarom niet aan het Pauli-uitsluitingsprincipe.
Dan bezetten alle helium-4-atomen bij temperaturen onder 2,2 K dezelfde kwantumtoestand en daarom is er maar één mogelijke microstaat, wat impliceert dat superfluïde helium-4 S = 0 heeft.
Opgeloste oefeningen
- Oefening 1
Laten we eens kijken naar een eenvoudig geval dat bestaat uit een systeem dat bestaat uit slechts drie deeltjes met drie energieniveaus. Voor dit eenvoudige systeem:
a) Bepaal het aantal mogelijke microstaten voor drie temperatuurbereiken:
-hoog
-Voor de helft
-Kort
b) Bepaal met behulp van de Boltzmann-vergelijking de entropie in de verschillende temperatuurbereiken.
c) Bespreek de resultaten en leg uit of ze in strijd zijn met de derde wet van de thermodynamica..
Oplossing voor
Op moleculaire en atomaire schaal worden de energieën die een systeem kan aannemen gekwantiseerd, wat betekent dat ze alleen bepaalde discrete waarden kunnen aannemen. Bovendien, wanneer de temperaturen zo laag zijn, hebben de deeltjes waaruit het systeem bestaat alleen de mogelijkheid om de laagste energieniveaus te bezetten..
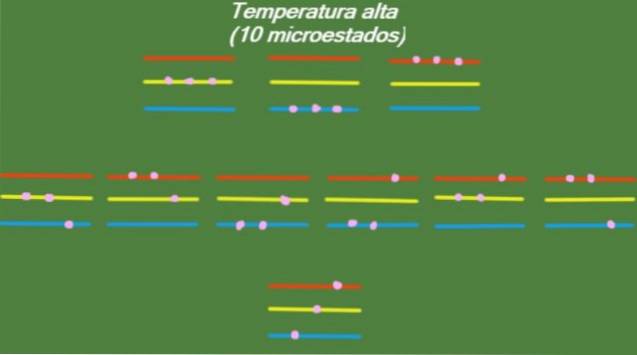
Hoge temperatuur
Als het systeem een relatief hoge temperatuur T heeft, hebben de deeltjes genoeg energie om alle beschikbare niveaus te bezetten, waardoor 10 mogelijke microstates ontstaan, die in de volgende afbeelding verschijnen:
Medium temperatuur
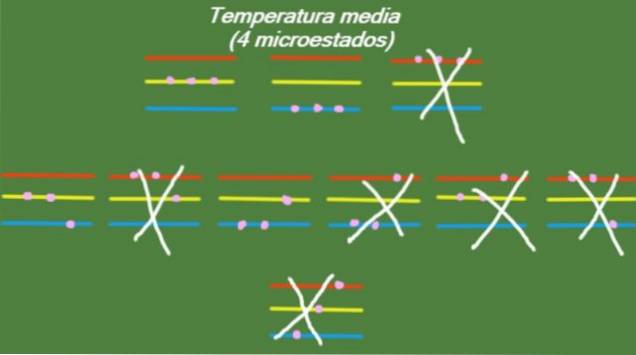
In het geval dat het systeem een tussenliggende temperatuur heeft, hebben de deeltjes waaruit het bestaat niet genoeg energie om het hoogste energieniveau te bezetten. De mogelijke microstates worden geïllustreerd in de figuur:
Lage temperatuur
Als de temperatuur blijft dalen in ons geïdealiseerde systeem van drie deeltjes en drie energieniveaus, dan zullen de deeltjes zo weinig energie hebben dat ze alleen het laagste niveau kunnen innemen. In dit geval blijft er slechts 1 mogelijke microstaat over, zoals weergegeven in figuur 6:
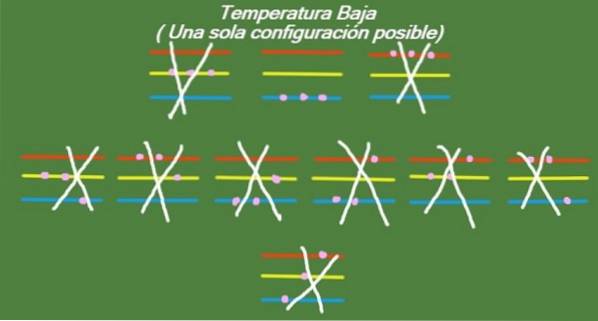
Oplossing b
Zodra het aantal microstaten in elk temperatuurbereik bekend is, kunnen we nu de Boltzmann-vergelijking hierboven gebruiken om de entropie in elk geval te vinden.
S = k ln (10) = 2,30 x k = 3,18 x 10-2. 3 J / K (Hoge temperatuur)
S = k ln (4) = 1,38 x k = 1,92 x 10-2. 3 J / K (Medium temperatuur)
En tenslotte:
S = k ln (1) = 0 (Lage temperatuur)
Oplossing c
Ten eerste merken we dat de entropie afneemt naarmate de temperatuur daalt, zoals verwacht. Maar voor de laagste temperatuurwaarden wordt een drempelwaarde bereikt, van waaruit de basistoestand van het systeem wordt bereikt..
Zelfs als de temperatuur zo dicht mogelijk bij het absolute nulpunt ligt, zijn er geen lagere energietoestanden beschikbaar. Dan houdt de entropie zijn minimumwaarde constant, die in ons voorbeeld S = 0 is.
Deze oefening illustreert, op het niveau van de microstaat van een systeem, de reden waarom de derde wet van de thermodynamica geldt..
- Oefening 2
Reden of de volgende bewering waar of onwaar is:
"De entropie van een systeem bij het absolute nulpunt is precies nul".
Motiveer uw antwoord en beschrijf enkele voorbeelden.
Oplossing
Het antwoord is: vals.
In de eerste plaats kan de absolute 0 van temperatuur niet worden bereikt omdat dit in strijd zou zijn met het onzekerheidsprincipe van Heisenberg en de derde wet van de thermodynamica..
Het is erg belangrijk op te merken dat de derde wet niet zegt wat er gebeurt bij absoluut 0, maar eerder wanneer de temperatuur oneindig dicht bij het absolute 0 ligt. Het verschil is subtiel, maar significant.
Evenmin bevestigt de derde wet dat wanneer de temperatuur een waarde aanneemt die willekeurig dicht bij het absolute nulpunt ligt, de entropie naar nul neigt. Dit zou alleen gebeuren in het geval dat eerder werd geanalyseerd: het perfecte kristal, dat een idealisatie is.
Veel systemen op microscopische schaal, dat wil zeggen op kwantumschaal, hebben hun basisniveau van energie ontaarden, wat betekent het bestaan van verschillende instellingen op het laagste energieniveau.
Dit betekent dat in deze systemen de entropie nooit exact nul zou zijn. Evenmin zou de entropie exact nul zijn in systemen die vitrificeren wanneer de temperatuur naar het absolute nulpunt neigt. In dit geval is het resterende entropie eerder gezien.
Het is te wijten aan het feit dat de moleculen ervan "vastzaten" voordat ze de laagste beschikbare energieniveaus bereikten, waardoor het aantal mogelijke microstaten aanzienlijk toeneemt, waardoor het onmogelijk wordt dat de entropie exact nul is..
Referenties
- Cengel, Y. 2012. Thermodynamica. 7e editie. McGraw Hill. 347.
- Jet Propulsion Laboratory. De coolste plek in het heelal. Teruggeplaatst van: coldatomlab.jpl.nasa.gov.
- González, A. Entropie en spontaniteit. Hersteld van: geocities.ws
- Quora. Wat is het praktische gebruik van de derde wet van de thermodynamica? Hersteld van: quora.com
- Algemene scheikunde. Derde principe van thermodynamica. Hersteld van: corinto.pucp.edu.pe
- Derde wet van de thermodynamica. Hersteld van: youtube.com
- Wikipedia. Resterende entropie. Hersteld van: en.wikipedia.com
- Wikipedia. Derde wet van de thermodynamica. Hersteld van: en.wikipedia.com



Niemand heeft nog op dit artikel gereageerd.