De Pascal's vat Het was een experiment dat de Franse wetenschapper Blaise Pascal in 1646 uitvoerde om definitief aan te tonen dat de druk van een vloeistof zich er op dezelfde manier doorheen voortplant, ongeacht de vorm van de container..
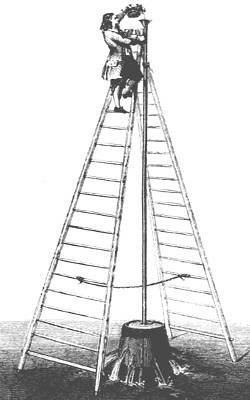
Het experiment bestaat uit het vullen van een vat met een dunne en zeer hoge buis, perfect aangepast aan de vulhals. Wanneer de vloeistof een hoogte van ongeveer 10 meter bereikt (hoogte komt overeen met 7 gestapelde vaten) barst het vat door de druk die wordt uitgeoefend door de vloeistof in de smalle buis.
De sleutel tot het fenomeen is om het concept van druk te begrijpen. De druk P. uitgeoefend door een vloeistof op een oppervlak is de totale kracht F. op dat oppervlak gedeeld door het gebied NAAR van genoemd oppervlak:
P = F / A
Artikel index
Laten we, om de fysische principes van het experiment van Pascal te begrijpen, de druk berekenen op de bodem van een wijnvat dat zich met water zal vullen. Voor meer eenvoud van de berekeningen gaan we ervan uit dat het cilindrisch is met de volgende afmetingen: diameter 90 cm en hoogte 130 cm.
Zoals gezegd, de druk P. diep van binnen is de totale kracht F. op de achtergrond, gedeeld door het gebied NAAR Van de bodem:
P = F / A
Het gebied NAAR vanaf de onderkant is pi keer (π≈3.14) de radio R vanaf de onderkant in het kwadraat:
A = π⋅R ^ 2
In het geval van het vat is het 6362 cm ^ 2, wat overeenkomt met 0,6362 m ^ 2.
De kracht F. op de bodem van de ton staat het gewicht van het water. Dit gewicht kan worden berekend door de dichtheid te vermenigvuldigen ρ van water door het watervolume en door de versnelling van de zwaartekracht g.
F = ρ⋅A⋅h⋅g
In het geval van het vat vol water hebben we:
F = ρ⋅A⋅h⋅g = 1000 (kg / m ^ 3) ⋅0,6362 m ^ 2⋅1,30 m⋅10 (m / s ^ 2) = 8271 N.
De kracht is berekend in newton en komt overeen met 827 kg-f, een waarde die vrij dicht bij één ton ligt. De druk aan de onderkant van het vat is:
P = F / A = 8271 N / 0,6362 m ^ 2 = 13000 Pa = 13 kPa.
De druk is berekend in Pascal (Pa), de drukeenheid in het internationale SI-meetsysteem. Een atmosfeer van druk is gelijk aan 101325 Pa = 101,32 kPa.
Laten we eens kijken naar een kleine buis met een binnendiameter van 1 cm en een hoogte die gelijk is aan die van een vat, dat wil zeggen 1,30 meter. De buis wordt verticaal geplaatst met het onderste uiteinde afgedicht met een ronde dop en is aan het bovenste uiteinde gevuld met water.
Laten we eerst de oppervlakte van de onderkant van de buis berekenen:
A = π⋅R ^ 2 = 3,14 * (0,5 cm) ^ 2 = 0,785 cm ^ 2 = 0,0000785 m ^ 2.
Het gewicht van het water in de buis wordt berekend volgens de volgende formule:
F = ρ⋅A⋅h⋅g = 1000 (kg / m ^ 3) ⋅0,0000785 m ^ 2⋅1,30 m⋅10 (m / s ^ 2) = 1,0 N.
Dat wil zeggen dat het gewicht van water 0,1 kg-f is, dat wil zeggen slechts 100 gram.
Laten we nu de druk berekenen:
P = F / A = 1 N / 0,0000785 m ^ 2 = 13000 Pa = 13 kPa.
Verbazingwekkend! De druk is dezelfde als die van een vat. Dit is de hydrostatische paradox.
De druk op de bodem van het vat van Pascal is de som van de druk die wordt geproduceerd door het water in het vat zelf plus de druk van het water in een smalle buis van 9 meter hoog en 1 cm in diameter die is verbonden met de mond. vat vulling.
P = F / A = ρ⋅A⋅h⋅g / A = ρ⋅g⋅h = 1000 * 10 * 9 Pa = 90000 Pa = 90 kPa.
Merk op dat in de vorige uitdrukking het gebied NAAR het is geannuleerd, ongeacht of het een groot of klein gebied is zoals de buis. Met andere woorden, de druk is afhankelijk van de hoogte van het oppervlak ten opzichte van de bodem, ongeacht de diameter..
Laten we aan deze druk de druk van het vat zelf eronder toevoegen:
P.tot = 90 kPa + 13 kPa = 103 kPa.
Om erachter te komen hoeveel kracht er op de bodem van het vat wordt uitgeoefend, vermenigvuldigen we de totale druk met het oppervlak van de bodem van het vat.
F.tot = P.tot * A = 103000 Pa * 0,6362 m ^ 2 = 65529 N = 6553 kg-f.
Dit betekent dat de onderkant van de loop 6,5 ton gewicht draagt.
Het vatexperiment van Pascal is thuis gemakkelijk reproduceerbaar, mits het op kleinere schaal wordt gedaan. Hiervoor is het niet alleen nodig om de afmetingen te verkleinen, maar ook om het vat te vervangen door een glas of container die minder drukvast is..
1- Een wegwerpbeker van polystyreen met deksel. Volgens het Spaanssprekende land wordt polystyreen op verschillende manieren genoemd: witte kurk, piepschuim, piepschuim, schuim, anime en andere namen. Deze deksels zijn vaak te vinden bij afhaalrestaurants..
2- Plastic slang, bij voorkeur transparant 0,5 cm in diameter of kleiner en tussen 1,5 en 1,8 m lang.
3- Plakband voor verpakking.
- Prik met behulp van een boor, met een pons, een scheermes of een mesje in het deksel van de piepschuim beker, zodat er een gaatje wordt gemaakt waar de slang strak doorheen gaat.
- Leid de slang door het gat in het deksel, zodat een klein deel van de slang in het glas komt.
- Dicht de verbinding van de slang netjes af met tape en pak de dop aan beide zijden van de dop.
- Plaats het deksel op het glas en dicht ook de voeg tussen het deksel en het glas af met verpakkingstape, zodat er geen water kan ontsnappen.
- Leg het glas op de grond en dan moet je de slang uitrekken en optillen. Het kan handig zijn om op te staan met een druppel, een kruk of een ladder.
- Vul het glas met water via de slang. Het kan worden geholpen door een kleine trechter aan het uiteinde van de slang om het vullen te vergemakkelijken.
Als het glas vol is en het waterpeil door de slang begint te stijgen, neemt de druk toe. Er komt een tijd dat het polystyreenglas de druk niet weerstaat en barst, zoals Pascal demonstreerde met zijn beroemde vat.
Niemand heeft nog op dit artikel gereageerd.