
Acute Triangle-kenmerken en -typen

De acute driehoeken zijn die waarvan de drie interne hoeken scherpe hoeken zijn; dat wil zeggen, de maat van elk van deze hoeken is minder dan 90 ° graden. Door geen rechte hoek te hebben, hebben we dat de stelling van Pythagoras niet geldt voor deze geometrische figuur.
Daarom, als we informatie willen hebben over een van de zijden of hoeken, is het noodzakelijk om gebruik te maken van andere stellingen die ons toegang geven tot de genoemde gegevens. Degenen die we kunnen gebruiken zijn de sinusstelling en de cosinusstelling.
Artikel index
- 1 Kenmerken
- 1.1 Sinusstelling
- 1.2 Cosinusstelling
- 2 soorten
- 2.1 Gelijkzijdige acute driehoeken
- 2.2 Gelijkbenige acute driehoeken
- 2.3 Scalene acute driehoeken
- 3 Resolutie van acute driehoeken
- 3.1 Voorbeeld 1
- 3.2 Voorbeeld 2
Kenmerken
Onder de kenmerken die deze geometrische figuur heeft, kunnen we de kenmerken benadrukken die worden gegeven door het simpele feit dat hij een driehoek is. Onder deze hebben we:
- Een driehoek is een veelhoek met drie zijden en drie hoeken.
- De som van de drie interne hoeken is gelijk aan 180 °.
- De som van twee zijden is altijd groter dan de derde.
Laten we als voorbeeld eens kijken naar de volgende driehoek ABC. In het algemeen identificeren we de zijden met een kleine letter en de hoeken met een hoofdletter, zodanig dat de ene zijde en de tegenoverliggende hoek dezelfde letter hebben..
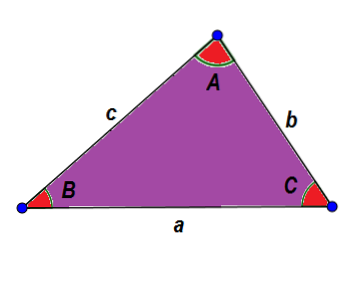
Van de reeds gegeven kenmerken weten we dat:
A + B + C = 180 °
a + b> c, a + c> b en b + c> a
Het belangrijkste kenmerk dat dit type driehoek van de rest onderscheidt, is dat, zoals we al zeiden, de interne hoeken scherp zijn; dat wil zeggen, de maat van elk van zijn hoeken is minder dan 90 °.
Scherpe driehoeken, samen met stompe driehoeken (die waarin een van hun hoeken een maat groter dan 90 ° heeft), maken deel uit van de reeks schuine driehoeken. Deze set bestaat uit de driehoeken die geen rechte hoeken zijn.
Omdat de schuine driehoeken deel uitmaken, moeten we problemen met acute driehoeken kunnen oplossen, we moeten gebruik maken van de sinusstelling en de cosinusstelling.
Sinusstelling
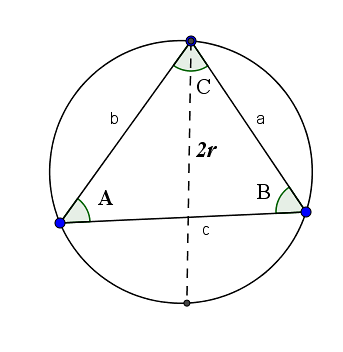
De sinusstelling vertelt ons dat de verhouding van een zijde tot de sinus van zijn tegengestelde hoek gelijk is aan tweemaal de straal van de cirkel die wordt gevormd door de drie hoekpunten van die driehoek. Namelijk:
2r = a / sin (A) = b / sin (B) = c / sin (C)
Cosinus stelling
Aan de andere kant geeft de cosinusstelling ons deze drie gelijkheden voor elke driehoek ABC:
naartwee= btwee + ctwee -2bc * cos (A)
btwee= eentwee + ctwee -2ac * cos (B)
ctwee= eentwee + btwee -2ab * cos (C)
Deze stellingen staan ook bekend als respectievelijk de wet van de sinus en de wet van de cosinus..
Een ander kenmerk dat we van de acute driehoeken kunnen geven, is dat twee ervan gelijk zijn als ze aan een van de volgende criteria voldoen:
- Als ze alle drie gelijke kanten hebben.
- Als ze één zijde en twee gelijke hoeken ten opzichte van elkaar hebben.
- Als ze twee gelijke zijden en een hoek hebben.
Types
We kunnen acute driehoeken classificeren op basis van hun zijden. Deze kunnen zijn:
Gelijkzijdige acute driehoeken
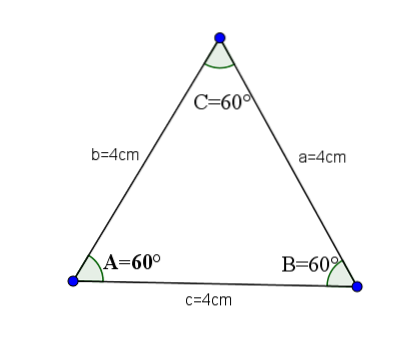
Het zijn de scherpe driehoeken waarvan al hun zijden gelijk zijn en daarom hebben al hun interne hoeken dezelfde waarde, namelijk A = B = C = 60 ° graden.
Laten we als voorbeeld de volgende driehoek nemen, waarvan de zijden a, b en c de waarde 4 hebben.
Gelijkbenige acute driehoeken
Deze driehoeken hebben, naast scherpe interne hoeken, het kenmerk dat ze twee van hun gelijke zijden hebben en de derde, die over het algemeen als basis wordt genomen, anders.
Een voorbeeld van dit type driehoek kan er een zijn waarvan de basis 3 is en de andere twee zijden een waarde van 5 hebben. de basis zou 34,9 ° zijn.
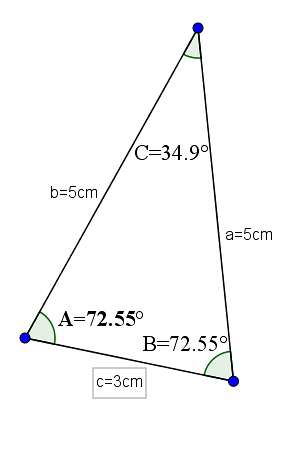
Scalene acute driehoeken
Dit zijn de driehoeken die allemaal twee aan twee verschillende zijden hebben. Daarom zijn alle hoeken, behalve dat ze kleiner zijn dan 90 °, verschillend van twee tot twee.
De driehoek DEF (waarvan de afmetingen d = 4, e = 5 en f = 6 zijn en de hoeken D = 41,41 °, E = 55,79 ° en F = 82,8 °) is een goed voorbeeld van een acute driehoeksschaal.
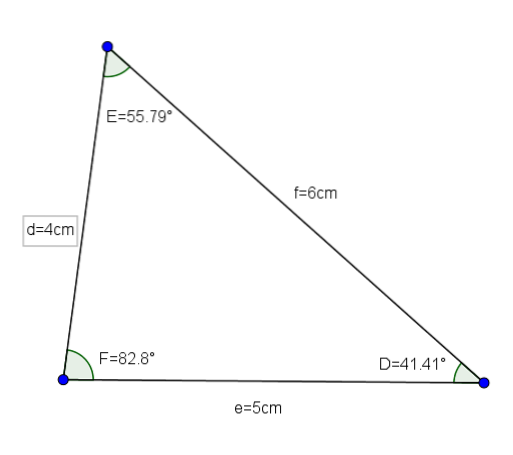
Resolutie van acute driehoeken
Zoals we eerder zeiden, is het voor het oplossen van problemen met acute driehoeken noodzakelijk om de sinus- en cosinusstellingen te gebruiken.
voorbeeld 1
Gegeven een driehoek ABC met hoeken A = 30 °, B = 70 ° en zijde a = 5 cm, willen we de waarde van hoek C en zijden b en c weten.
Het eerste dat we doen, is het feit gebruiken dat de som van de interne hoeken van een driehoek 180 ° is, om de waarde van hoek C te verkrijgen.
180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C
We wissen C en we blijven achter met:
C = 180 ° - 100 ° = 80 °
Omdat we de drie hoeken en één zijde al kennen, kunnen we de sinusstelling gebruiken om de waarde van de overige zijden te bepalen. Volgens de stelling hebben we:
a / sin (A) = b / sin (B) en a / sin (A) = c / (sin (C)
We isoleren b uit de vergelijking en we houden over:
b = (a * sin (B)) / sin (A) ≈ (5 * 0,940) / (0,5) ≈ 9,4
Nu hoeven we alleen de waarde van c te berekenen. We gaan op dezelfde manier te werk als in het vorige geval:
c = (a * sin (C)) / sin (A) ≈ (5 * 0,984) / (0,5) ≈ 9,84
Zo verkrijgen we alle gegevens van de driehoek. Zoals we kunnen zien, valt deze driehoek in de categorie van scalene acute driehoek.
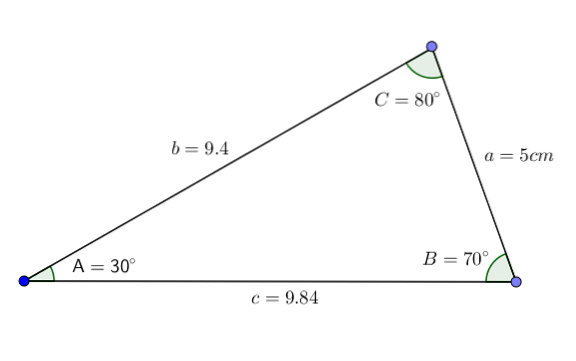
Voorbeeld 2
Gegeven een driehoek DEF met zijden d = 4 cm, e = 5 cm en f = 6 cm, willen we de waarde van de hoeken van die driehoek weten.
Voor dit geval zullen we de cosinuswet gebruiken, die ons vertelt dat:
dtwee= etwee + F.twee - 2efcos (D)
Uit deze vergelijking kunnen we cos (D) oplossen, wat ons als resultaat geeft:
Cos (D) = ((4)twee - (5)twee -(6)twee) / (- 2 * 5 * 6) = 0,75
Daarom hebben we D≈ 41,41 °
Nu we de senom-stelling gebruiken, hebben we de volgende vergelijking:
d / (sin (D) = e / (sin (E)
Oplossend voor zonde (E), hebben we:
sin (E) = e * sin (D) / d = (5 * 0,66) / 4 ≈ 0,827
Daarom hebben we E≈55,79 °
Als we tenslotte gebruiken dat de som van de binnenhoeken van een driehoek 180 ° is, hebben we die F≈82,8 °.
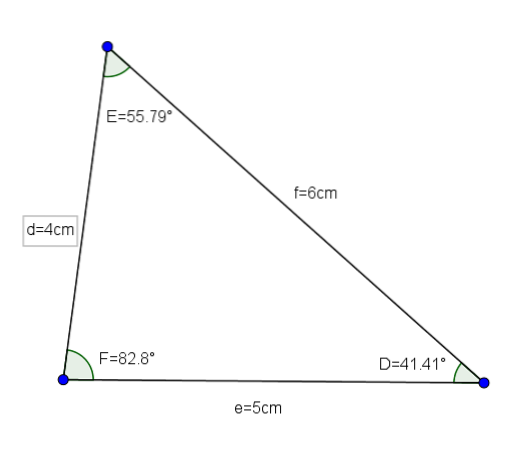
- Landaverde, F. d. (1997). Geometry (herdruk red.). Vooruitgang.
- Leake, D. (2006). Driehoeken (geïllustreerd red.). Heinemann-Raintree.
- Leal G. Juan Manuel. (2003). Metrische meetkunde voor vlakken. CODEPRE
- Ruiz, Á., & Barrantes, H. (2006). Geometrieën. CR-technologie.
- Sullivan, M. (1997). Goniometrie en analytische meetkunde. Pearson Education.



Niemand heeft nog op dit artikel gereageerd.