De driehoeken Het zijn platte en gesloten geometrische figuren, bestaande uit drie zijden. Een driehoek wordt bepaald door drie lijnen die twee aan twee snijden en drie hoeken met elkaar vormen. De driehoekige vorm, vol symboliek, is aanwezig in talloze objecten en als constructie-element.
De oorsprong van de driehoek is verloren gegaan in de geschiedenis. Uit archeologisch bewijs is bekend dat de primitieve mensheid het goed kende, aangezien archeologische overblijfselen bevestigen dat het werd gebruikt in gereedschappen en wapens.
Het is ook duidelijk dat de oude Egyptenaren een gedegen kennis hadden van geometrie en in het bijzonder van de driehoekige vorm. Ze kwamen tot uiting in de architectonische elementen van de monumentale gebouwen.
In de Rhind-papyrus zijn formules voor de berekening van gebieden van driehoeken en trapezoïden, evenals enkele volumes en andere concepten van rudimentaire trigonometrie.
Van hun kant is bekend dat de Babyloniërs in staat waren om de oppervlakte van de driehoek en andere geometrische figuren te berekenen, die ze gebruikten voor praktische doeleinden, zoals landverdelingen. Ze waren ook goed op de hoogte van veel eigenschappen van driehoeken.
Het waren echter de oude Grieken die veel van de geometrische concepten die tegenwoordig heersen, hebben gesystematiseerd, hoewel veel van deze kennis niet exclusief was, aangezien het zeker werd gedeeld met deze andere oude beschavingen..
Artikel index
De elementen van elke driehoek worden aangegeven in de volgende afbeelding. Er zijn drie: hoekpunten, zijden en hoeken.
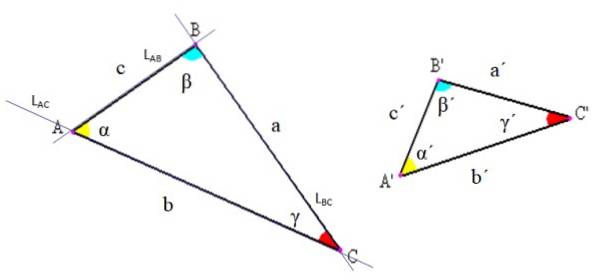
-Hoekpunten: zijn de snijpunten van de lijnen waarvan de segmenten de driehoek bepalen. In bovenstaande figuur staat bijvoorbeeld de lijn LAC met segment AC, snijdt lijn LAB met segment AB net op punt A.
-Zijkanten: tussen elk paar hoekpunten wordt een lijnstuk getekend dat één zijde van de driehoek vormt. Dit segment kan worden aangeduid met de eindletters of door een specifieke letter te gebruiken om het te noemen. In het voorbeeld in figuur 2 wordt zijde AB ook wel "c" genoemd.
-Hoeken: Tussen elke zijde met een gemeenschappelijke top ontstaat een hoek, waarvan de top samenvalt met die van de driehoek. Over het algemeen wordt de hoek aangegeven met een Griekse letter, zoals in het begin werd gezegd.
Om een bepaalde driehoek met een bepaalde vorm en grootte te bouwen, hoeft u alleen maar een van de volgende gegevenssets te hebben:
-Alle drie de zijden, vrij duidelijk voor een driehoek.
-Twee zijden en de hoek ertussen, en onmiddellijk wordt de overgebleven zijde getekend.
-Twee (interne) hoeken en de zijde ertussen. Bij uitbreiding worden de twee ontbrekende zijden getekend en is de driehoek klaar.
Over het algemeen worden in driehoeksnotatie de volgende conventies gebruikt: hoekpunten worden aangegeven met Latijnse hoofdletters, zijden met Latijnse letters in kleine letters en hoeken met Griekse letters (zie figuur 2).
Op deze manier wordt de driehoek genoemd naar zijn hoekpunten. De driehoek aan de linkerkant in figuur 2 is bijvoorbeeld driehoek ABC en die aan de rechterkant is driehoek A'B'C '.
Het is ook mogelijk om andere notaties te gebruiken; de hoek a in figuur 2 wordt bijvoorbeeld aangeduid als BAC. Merk op dat de letter van het hoekpunt in het midden staat en dat de letters tegen de klok in worden geschreven.
Andere keren wordt een caret geplaatst om de hoek aan te duiden:
α = ∠A
Er zijn verschillende criteria voor het classificeren van driehoeken. Het meest gebruikelijke is om ze te classificeren volgens de maat van hun zijden of volgens de maat van hun hoeken. Afhankelijk van de grootte van hun zijden, kunnen de driehoeken zijn: schalen, gelijkbenig of gelijkzijdig:
-Scalene: de drie kanten zijn verschillend.
-Gelijkbenig: heeft twee gelijke kanten en een andere kant.
-Gelijkzijdig: alle drie de zijden zijn gelijk.
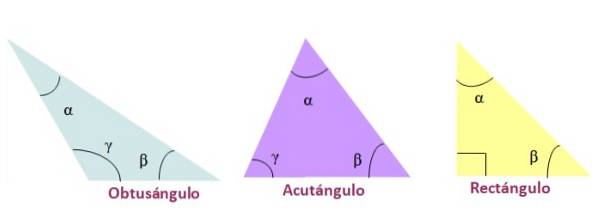
Volgens de maat van hun hoeken worden de driehoeken als volgt genoemd:
-Stompe hoek, als een van de interne hoeken groter is dan 90º.
-Scherpe hoek, wanneer de drie interne hoeken van de driehoek scherp zijn, dat wil zeggen minder dan 90 °
-Rechthoek, in het geval dat een van de interne hoeken 90º is. De zijkanten die 90º vormen worden benen genoemd en de kant tegenover de rechte hoek is de hypotenusa..
Wanneer twee driehoeken dezelfde vorm hebben en dezelfde grootte hebben, wordt gezegd dat ze congruent zijn. Natuurlijk is congruentie gerelateerd aan gelijkheid, dus waarom spreken we in de meetkunde over 'twee congruente driehoeken' in plaats van 'twee gelijke driehoeken'?
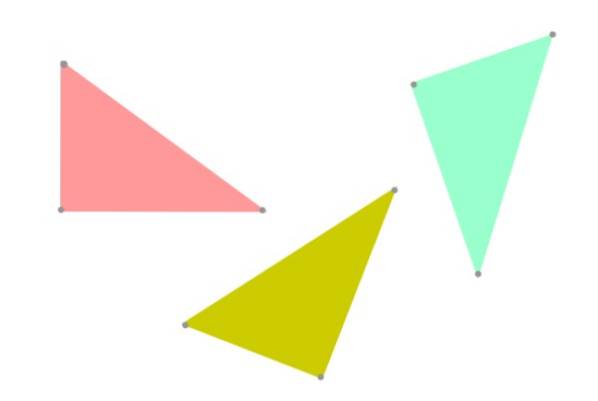
Welnu, het verdient de voorkeur om de term "congruentie" te gebruiken om vast te houden aan de waarheid, aangezien twee driehoeken dezelfde vorm en grootte kunnen hebben, maar anders in het vlak georiënteerd zijn (zie figuur 3). Vanuit het oogpunt van geometrie zouden ze niet langer strikt hetzelfde zijn.
Twee driehoeken zijn congruent als een van de volgende situaties zich voordoet:
-Alle drie de zijden meten hetzelfde (nogmaals, dit is het meest voor de hand liggend).
-Ze hebben twee identieke zijden en met dezelfde hoek ertussen.
-Beide hebben twee identieke interne hoeken en de zijde tussen deze hoeken meet hetzelfde.
Zoals te zien is, gaat het erom dat de twee driehoeken aan de noodzakelijke voorwaarden voldoen, zodat wanneer ze worden gebouwd, hun vorm en grootte precies hetzelfde zijn..
De congruentiecriteria zijn erg handig, omdat in de praktijk ontelbare stukken en mechanische onderdelen in serie moeten worden vervaardigd, zodanig dat hun afmetingen en vorm exact hetzelfde zijn.
Een driehoek is vergelijkbaar met een andere als ze dezelfde vorm hebben, ook al hebben ze verschillende afmetingen. Om ervoor te zorgen dat de vorm hetzelfde is, is het vereist dat de interne hoeken dezelfde waarde hebben en dat de zijkanten proportioneel zijn..
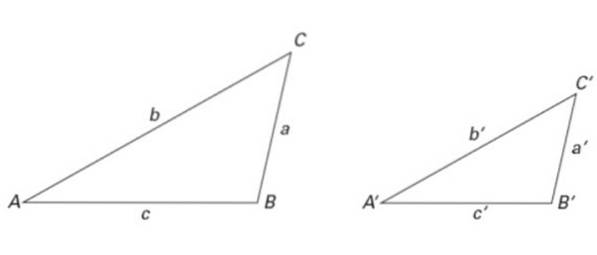
De driehoeken in figuur 2 zijn ook vergelijkbaar, net als die in figuur 6. Op deze manier:
∠ A = ∠ A ', ∠ B = ∠ B 'en ∠ C = C '
Met betrekking tot de zijkanten gelden de volgende gelijkenisverhoudingen:
a / a '= b / b' = c / c '
De fundamentele eigenschappen van driehoeken zijn als volgt:
-De som van de binnenhoeken van elke driehoek is altijd 180º.
-Voor elke driehoek is de som van de buitenhoeken gelijk aan 360 °.
- Een uitwendige hoek van een driehoek is gelijk aan de som van de twee binnenhoeken die niet aan die hoek grenzen.
Ze worden toegeschreven aan de Griekse filosoof en wiskundige Thales van Miletus, die verschillende stellingen met betrekking tot meetkunde ontwikkelde. De eerste stelt het volgende vast:
Als meerdere parallelle lijnen twee dwarslijnen snijden, worden daarin proportionele segmenten bepaald.
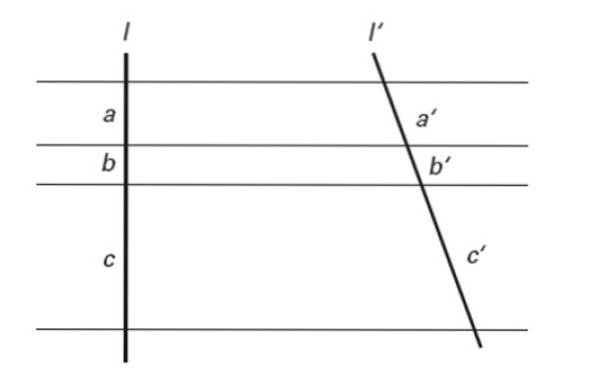
Met andere woorden:
a / a '= b / b' = c / c '
De eerste stelling van Thales is van toepassing op een driehoek, we hebben bijvoorbeeld de blauwe driehoek ABC aan de linkerkant, die wordt doorgesneden door de rode parallellen aan de rechterkant:
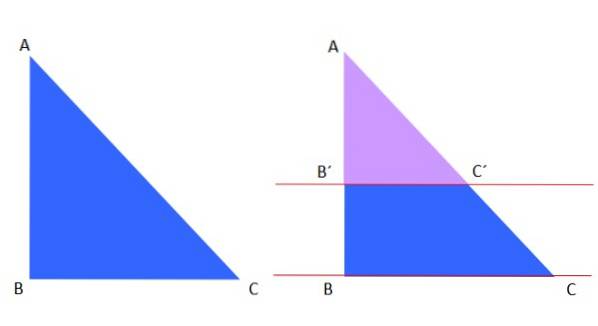
De violette driehoek AB'C 'lijkt op de blauwe driehoek ABC, daarom kan volgens de stelling van Thales het volgende worden geschreven:
AB '/ AC' = AB / AC
En het is consistent met wat eerder werd uitgelegd in het segment van de gelijkenis van driehoeken. Overigens kunnen parallelle lijnen ook verticaal of parallel aan de hypotenusa zijn en soortgelijke driehoeken worden op dezelfde manier verkregen.
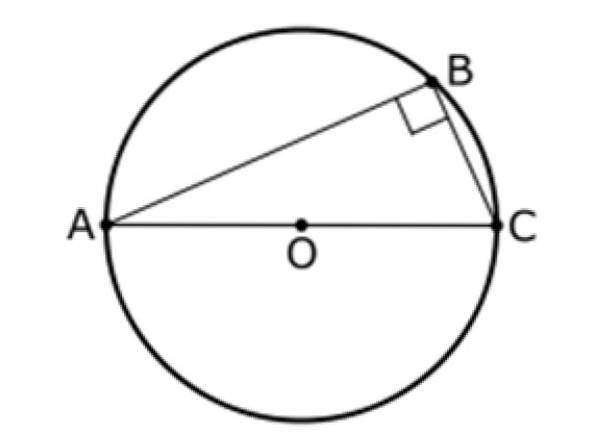
Deze stelling verwijst ook naar een driehoek en een cirkel met middelpunt O, zoals hieronder weergegeven. In deze figuur is AC een diameter van de omtrek en is B een punt erop, waarbij B verschilt van A en B.
Thales 'tweede stelling stelt dat:
De hoek tussen de segmenten AB en BC is altijd 90º, dus de driehoek ABC heeft gelijk.
Dit is een van de beroemdste stellingen in de geschiedenis. Het is te danken aan de Griekse wiskundige Pythagoras van Samos (569 - 475 v.Chr.) En is van toepassing op een rechthoekige driehoek. Zegt het:
De som van de vierkanten van de lengtes van de benen van de rechthoekige driehoek is gelijk aan de lengte van de hypotenusa in het kwadraat.
Als we als voorbeeld de blauwe driehoek in figuur 8 nemen, of de violette driehoek, aangezien beide rechthoeken zijn, dan kan worden gesteld dat:
ACtwee = ABtwee + BCtwee (blauwe driehoek)
AC 'twee = AB 'twee + BC 'twee (paarse driehoek)
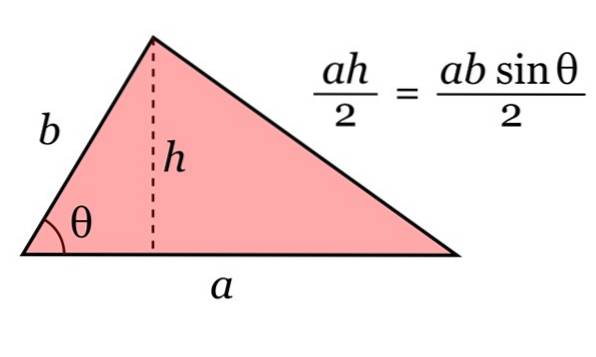
De oppervlakte van de driehoek wordt gegeven door het product van de basis naar en je lengte h, gedeeld door 2. En door trigonometrie kan deze hoogte worden geschreven als h = b sinθ.
Er wordt gezegd dat Thales er door middel van zijn eerste stelling in slaagde om de hoogte van de Grote Piramide in Egypte, een van de 7 wonderen van de antieke wereld, te meten door de schaduw te meten die op de grond werd geprojecteerd en die werd geprojecteerd door een paal. in de grond gedreven..
Dit is de schets van de procedure die wordt gevolgd door Tales:
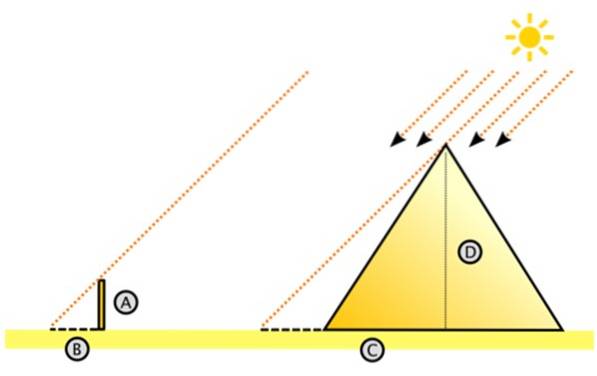
Thales nam terecht aan dat de zonnestralen parallel schijnen. Met dit in gedachten stelde hij zich de grote rechthoekige driehoek aan de rechterkant voor.
Daar is D de hoogte van de piramide en C is de afstand boven de grond gemeten vanaf het midden tot de schaduw van de piramide op de woestijnbodem. Het is misschien omslachtig om C te meten, maar het is zeker gemakkelijker dan het meten van de hoogte van de piramide.
Aan de linkerkant is de kleine driehoek, met poten A en B, waarbij A de hoogte is van de paal die verticaal in de grond is gedreven en B de schaduw is die hij werpt. Beide lengtes zijn meetbaar, evenals C (C is gelijk aan de lengte van de schaduw + de halve lengte van de piramide).
Dus door gelijkenis van driehoeken:
A / B = D / C
En de hoogte van de Grote Piramide blijkt te zijn: D = C. (A / B)
Spanten in de civiele constructie zijn constructies die zijn gemaakt van gekruiste rechte dunne staven van hout of metaal, die in veel gebouwen als ondersteuning worden gebruikt. Ze worden ook wel roosters, spanten of roosters genoemd (truss in Engels).
In hen zijn de driehoeken altijd aanwezig, omdat de staven met elkaar zijn verbonden op punten die knooppunten worden genoemd en die kunnen worden vastgemaakt of gearticuleerd..
De methode die bekend staat als triangulatie maakt het mogelijk om de locatie van ontoegankelijke punten te bepalen door andere afstanden te kennen die gemakkelijker te meten zijn, op voorwaarde dat er een driehoek wordt gevormd die de gewenste locatie tussen de hoekpunten omvat..
In de volgende afbeelding willen we bijvoorbeeld weten waar het schip zich in de zee bevindt, aangeduid als B.
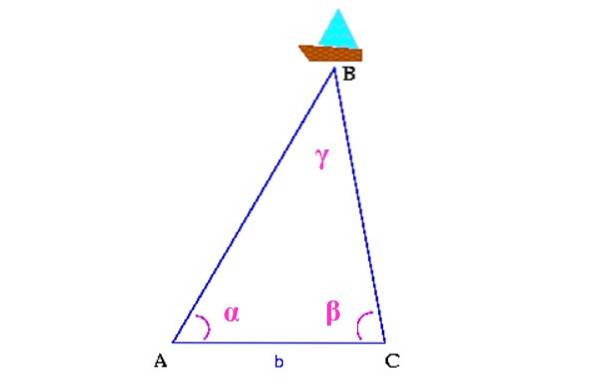
Eerst wordt de afstand tussen twee punten aan de kust gemeten, die in de figuur A en C zijn. Vervolgens moeten de hoeken α en β worden bepaald met behulp van een theodoliet, een apparaat dat wordt gebruikt om verticale en horizontale hoeken te meten.
Met al deze informatie wordt een driehoek gebouwd waarvan het bovenste hoekpunt het schip is. Het zou blijven om de hoek γ te berekenen met behulp van de eigenschappen van de driehoeken en de afstanden AB en CB met behulp van trigonometrie, om de positie van het schip in de zee te bepalen..
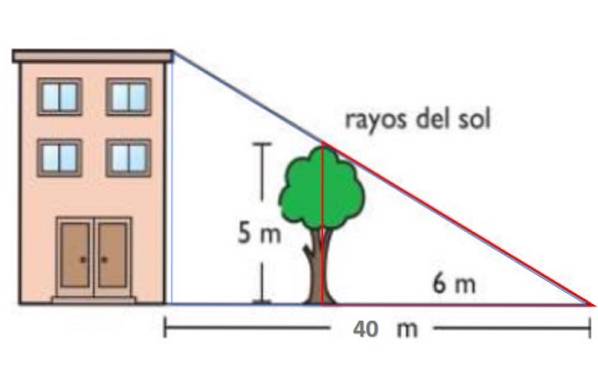
In de getoonde afbeelding zijn de zonnestralen parallel. Op deze manier werpt de 5 meter hoge boom een schaduw van 6 meter op de grond. Tegelijkertijd is de schaduw van het gebouw 40 meter. Volg de eerste stelling van Thales en zoek de hoogte van het gebouw.
De rode driehoek heeft zijden van respectievelijk 5 en 6 meter, terwijl de blauwe een hoogte H heeft - de hoogte van het gebouw - en een basis van 40 meter. Beide driehoeken lijken op elkaar, daarom:
H / 40 = 5/6 → H = 40. (5/6) m = 33,3 m
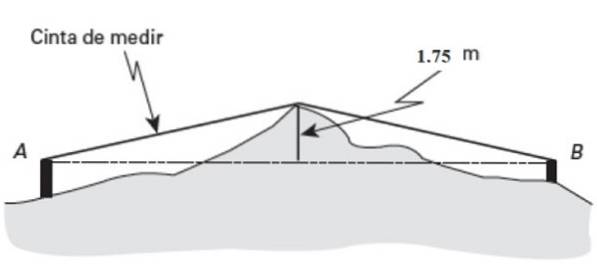
U moet de horizontale afstand tussen twee punten weten NAAR Y B, maar ze bevinden zich op een zeer oneffen ondergrond.
Ongeveer het middelpunt (Pm) van dit land valt op een prominente plaats van 1,75 meter hoog. Als het meetlint 26 meter lang aangeeft, gemeten van A tot uitsteeksel, en 27 meter van B tot hetzelfde punt, zoek dan de afstand AB.
De stelling van Pythagoras wordt toegepast op een van de twee rechthoekige driehoeken in de figuur. Beginnend met degene aan de linkerkant:
Hypotenusa = c = 26 meter
Hoogte = a = 1,75 meter
APm = (26twee - 1,75twee1/2 = 25,94 m
Breng nu Pythagoras aan in de driehoek aan de rechterkant, dit keer c = 27 meter, a = 1,75 meter. Met deze waarden:
BPm= (27twee - 1,75twee1/2 = 26,94 m
De afstand AB wordt gevonden door deze resultaten toe te voegen:
AB = 25,94 m + 26,94 m = 52,88 m.
Niemand heeft nog op dit artikel gereageerd.