
Ovale (geometrische figuur) kenmerken, voorbeelden, oefeningen
De ovaal symmetrisch wordt gedefinieerd als een vlakke en gesloten curve, die twee loodrechte symmetrie-assen heeft - een grote en een kleine - en bestaat uit twee omtrekbogen gelijk aan twee aan twee.
Op deze manier kan het worden getekend met behulp van een kompas en enkele referentiepunten op een van de symmetrielijnen. In ieder geval zijn er verschillende manieren om het te tekenen, zoals we later zullen zien.

Het is een zeer bekende curve, aangezien het wordt herkend als de contour van een ellips, dit is een specifiek geval van het ovaal. Maar het ovaal is geen ellips, hoewel het er soms erg op lijkt, omdat de eigenschappen en lay-out verschillen. De ellips is bijvoorbeeld niet geconstrueerd met een kompas.
Artikel index
- 1 Kenmerken
- 2 voorbeelden
- 2.1 Constructie van een ovaal met behulp van concentrische cirkels
- 3 oefeningen
- 3.1 - Oefening 1
- 3.2 - Oefening 2
- 4 referenties
Kenmerken
Het ovaal heeft zeer uiteenlopende toepassingen: architectuur, industrie, grafische vormgeving, uurwerken en sieraden zijn slechts enkele gebieden waar het gebruik ervan opvalt..
De meest opvallende kenmerken van deze belangrijke curve zijn de volgende:
-Het behoort tot de groep van technische curven: het wordt getekend door omtreksbogen te vormen met behulp van een kompas.
-Alle punten liggen op hetzelfde vlak.
-Mist bochten of lussen.
-De lay-out is continu.
-De ronding van het ovaal moet glad en bol zijn.
-Bij het tekenen van een lijn die het ovaal raakt, bevindt deze zich allemaal aan dezelfde kant van de lijn.
-Een ovaal laat maximaal twee raaklijnen toe.
Voorbeelden
Er zijn verschillende methoden om ovalen te construeren waarvoor een liniaal, vierkant en kompas nodig zijn. Dan gaan we enkele van de meest gebruikte noemen.
Constructie van een ovaal met behulp van concentrische cirkels
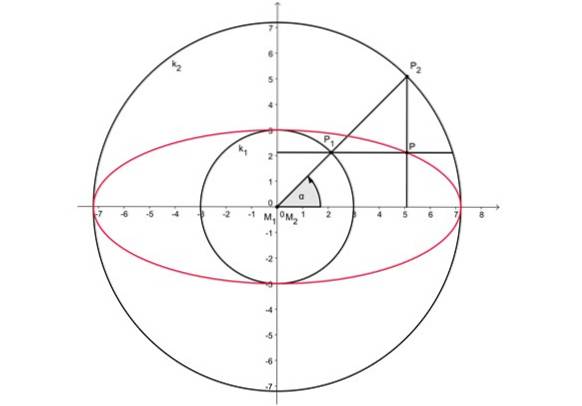
Figuur 2, hierboven, toont twee concentrische cirkels met het middelpunt van de oorsprong. De hoofdas van het ovaal meet hetzelfde als de diameter van de buitenomtrek, terwijl de secundaire as overeenkomt met de diameter van de binnenomtrek.
-Een willekeurige straal wordt naar de buitenomtrek getrokken, die beide cirkels op punten P snijdt1 En Ptwee.
-Dan wordt punt P geprojecteerdtwee op de horizontale as.
-Evenzo wordt het punt P geprojecteerd1 op de verticale as.
-Het snijpunt van beide projectielijnen is punt P en behoort tot het ovaal.
-Op deze manier kunnen alle punten in dit gedeelte van het ovaal worden uitgezet.
-De rest van het ovaal wordt getraceerd met de analoge procedure, uitgevoerd in elk kwadrant.
Opleiding
Vervolgens zullen andere manieren om ovalen te construeren worden onderzocht, gegeven een bepaalde initiële meting, die hun grootte zal bepalen..
- Oefening 1
Teken met behulp van een liniaal en een kompas een ovaal, bekend als de hoofdas, met een lengte van 9 cm.
Oplossing
In Afbeelding 3, hieronder weergegeven, wordt het resulterende ovaal in rood weergegeven. Speciale aandacht moet worden besteed aan de stippellijnen, de hulpconstructies die nodig zijn om een ovaal te tekenen waarvan de hoofdas is gespecificeerd. We gaan alle noodzakelijke stappen aangeven om tot de definitieve tekening te komen.
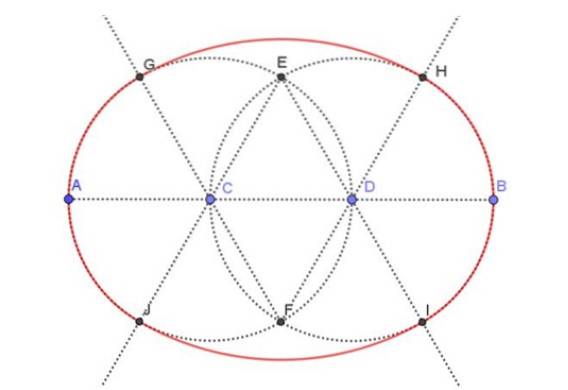
Stap 1
Teken met een liniaal het segment AB van 9 cm.
Stap 2
Trisect segment AB, dat wil zeggen, verdeel het in drie segmenten van gelijke lengte. Aangezien het oorspronkelijke segment AB 9 cm is, moeten de segmenten AC, CD en DB elk 3 cm meten.
Stap 3
Met het kompas, centrerend op C en opening CA, wordt een hulpomtrek getekend. Evenzo wordt de hulpomtrek met middelpunt D en straal DB getekend met het kompas..
Stap 4
De snijpunten van de twee hulpcirkels die in de vorige stap zijn gebouwd, zijn gemarkeerd. We noemen het punten E en F.
Stap 5
Met de regel worden de volgende stralen getekend: [FC), [FD), [EC), [ED).
Stap 6
De stralen van de vorige stap snijden de twee hulpcirkels op respectievelijk de punten G, H, I, J.
Stap 7
Met het kompas wordt het midden gemaakt in F en met de opening (of straal) FG wordt de boog getekend GH. Evenzo centrerend op E en straal EI, wordt de boog getekend IJ.
Stap 8
De vereniging van de bogen GJ, JI, IH Y HG vormen een ovaal waarvan de hoofdas 9 cm is.
Stap 9
We gaan verder met het wissen (verbergen) van de hulppunten en lijnen.
- Oefening 2
Teken een ovaal met een liniaal en een kompas, waarvan de secundaire as bekend is en de maat 6 cm is.
Oplossing
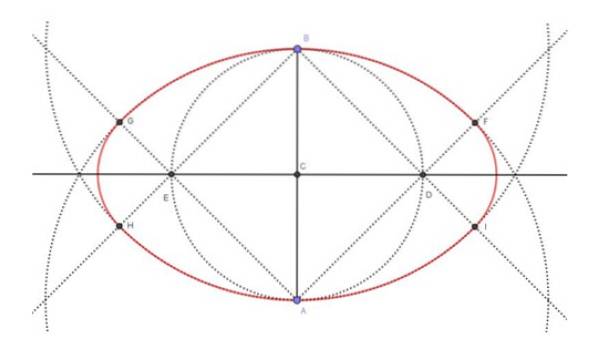
De figuur hierboven (figuur 4) toont het eindresultaat van de constructie van het ovaal (in rood), evenals de tussenconstructies die nodig zijn om het te bereiken. De stappen die werden gevolgd om het ovaal met de korte as van 6 cm te bouwen, waren als volgt:
Stap 1
Het 6 cm lange segment AB wordt getraceerd met de liniaal.
Stap 2
Met het kompas en de liniaal wordt de middelloodlijn getraceerd naar segment AB.
Stap 3
Het snijpunt van de middelloodlijn met segment AB resulteert in het middelpunt C van segment AB.
Stap 4
Met het kompas wordt de omtrek van middelpunt C en straal CA getekend.
Stap 5
De omtrek die in de vorige stap is getekend, snijdt de middelloodlijn van AB op de punten E en D.
Stap 6
De stralen [AD), [AE), [BD) en [BE) worden getekend.
Stap 7
Met het kompas worden de omtrekken van middelpunt A en straal AB en die van middelpunt B en straal BA getekend..
Stap 8
De snijpunten van de cirkels getekend in stap 7, met de stralen geconstrueerd in stap 6, bepalen vier punten, namelijk: F, G, H, I.
Stap 9
Met middelpunt op D en straal DI wordt de boog IF getekend. Op dezelfde manier wordt met middelpunt in E en straal EG de boog GH getekend.
Stap 10
De vereniging van de omtrekbogen FG, GH, HI en IF bepalen het gewenste ovaal.
Referenties
- Ed Plastic. Technische curven: ovalen, eivormige en spiralen. Hersteld van: drajonavarres.wordpress.com.
- Mathematische Basteleien. Eierkrommen en ovalen. Hersteld van: mathematische-basteleien.
- Universiteit van Valencia. Kegelsneden en platte technische curven. Hersteld van: ocw.uv.es.
- Wikipedia. Ovaal. Hersteld van: es.wikipedia.org.
- Wikipedia. Ovaal. Hersteld van: en.wikipedia.org.



Niemand heeft nog op dit artikel gereageerd.