Lineair variatieconcept, voorbeelden, opgeloste oefening

De lineaire variatie treedt op tussen twee fysieke grootheden wanneer de grafiek die ze vertegenwoordigt een rechte lijn is. Het komt overeen met bevestigen dat de variabelen lineair afhankelijk zijn, op een zodanige manier dat als we een van hen "y" en de andere "x" noemen, ze met elkaar in verband zullen worden gebracht door middel van de wiskundige uitdrukking:

y = mx + b

In deze formule zijn m en b reële getallen. De waarde van m staat voor de helling of inclinatie van de lijn -die altijd constant is- en b is de snede van de lijn met de verticale as.

Elk fenomeen dat reageert op een lineaire variatie heeft verschillende namen voor de variabelen, zoals we in de volgende voorbeelden zullen zien. De wiskundige vorm van de vergelijking is echter hetzelfde.

Experimenteel kan worden vastgesteld of er een lineair verband is tussen twee grootheden, waarbij de paren waarden (x, y) worden gemeten.

De aldus verkregen punten worden uitgezet op ruitjespapier en er wordt geobserveerd of ze een lineaire trend hebben, dat wil zeggen, of er een lijn is die voldoende past bij de experimentele gegevens.

Deze lijn kan in eerste instantie visueel worden getekend, maar door middel van een lineaire regressie analytisch te vinden zijn, de waarden van m en b van de lijn die het beste passen bij de experimentele punten.

Artikel index

• 1 Voorbeelden van lineaire variatie
  • 1.1 Snelheid in rechtlijnige beweging uniform gevarieerd
  • 1.2 Thermische uitzetting
  • 1.3 Positie van een mobiel met constante snelheid
  • 1.4 Hoogte van een persoon
  • 1.5 Temperatuurschalen
  • 1.6 Druk en diepte
• 2 Oefening opgelost
  • 2.1 Rijkosten
• 3 referenties

Voorbeelden van lineaire variatie

Er zijn tal van natuurlijke verschijnselen, evenals relaties tussen meetstandaarden, die het gevolg zijn van lineaire variatie, bijvoorbeeld:

Snelheid in rechtlijnige beweging werd uniform gevarieerd

De snelheid als functie van de tijd v (t) van een mobiel die langs een lijn beweegt met constante versnelling a en beginsnelheid v_of  anders dan 0. Deze beweging staat bekend als uniform gevarieerde rechtlijnige beweging en de vergelijking voor snelheid is:

v (t) = v_of + Bij

Thermische uitzetting

Een ander natuurlijk verschijnsel waarvan de variatie lineair is, is de toename in lengte die een staaf of draad ervaart bij verhitting..

Inderdaad, wanneer de temperatuur van een object toeneemt, nemen ook de afmetingen ervan toe, en deze toename hangt af van de verandering in temperatuur ΔT en een hoeveelheid genaamd lineaire uitzettingscoëfficiënt aangegeven met de Griekse letter α:

L = L_of + α ΔT

In deze uitdrukking is L de uiteindelijke lengte van het object en L_of is de aanvankelijke lengte.

Positie van een mobiel met constante snelheid

Een mobiel met snelheid constant beweegt altijd in een rechte lijn. Als de rechte lijn de horizontale x-as is, wordt de positie x (t) op elk moment gegeven door:

x (t) = x_of + ww

Waar x_of is de beginpositie, v is de snelheid en t is de tijd. Op deze manier wordt gezegd dat de positie x lineair varieert met de tijd t.

Hoogte van een persoon

Artsen en antropologen kunnen de lengte van een persoon schatten door de lengte van het dijbeen te meten..

Hoe groter een persoon is, hoe langer de benen zijn, dus er zijn lineaire modellen om de lengte van een volwassen H (in inches) te voorspellen als de lengte L (ook in inches) van zijn dijbeen bekend is, volgens de vergelijking:

H = 1.880⋅L + 32.010

Temperatuurschalen

De schalen van Celsius en Fahrenheit worden dagelijks gebruikt om temperaturen te meten. Deze laatste schaal wordt veel gebruikt in Engelssprekende landen. Er is een gelijkwaardigheid om van de een naar de ander te gaan:

F = (9/5) C + 32

Waar F de temperatuur is in graden Fahrenheit en C is de temperatuur in graden Celsius.

Druk en diepte

De absolute druk P in een onsamendrukbare vloeistof zoals water, waarvan de constante dichtheid ρ is, varieert als functie van diepte h als:

P = P_of + ρgh

Waar P_of is de druk op het vrije oppervlak van de vloeistof. Als de vloeistof zich in een container bevindt die open is naar de atmosfeer, is deze druk gewoon de atmosferische druk P_Geldautomaat, dan kunnen schrijven:

P = P_Geldautomaat + ρgh

De atmosferische druk op zeeniveau is ongeveer 101 kPa. Deze relatie tussen P en h betekent dat de druk lineair toeneemt met de diepte..

Oefening opgelost

Rijkosten

De maandelijkse kost C voor het besturen van een auto omvat een vaste maandelijkse kost C_of plus de kosten van elke maand afgelegde kilometers of gereden kilometers. Een bestuurder merkt op dat in een bepaalde maand de kosten van autorijden $ 380 voor 480 mijl waren, en de volgende maand $ 460 voor 800 mijl.

Laat d het aantal kilometers zijn dat de bestuurder per maand heeft afgelegd, met de verstrekte gegevens, zoek dan:

a) De lineaire variatie tussen C en d.

b) Hoeveel zou het per maand kosten om met de auto een rit van 1500 mijl te maken?

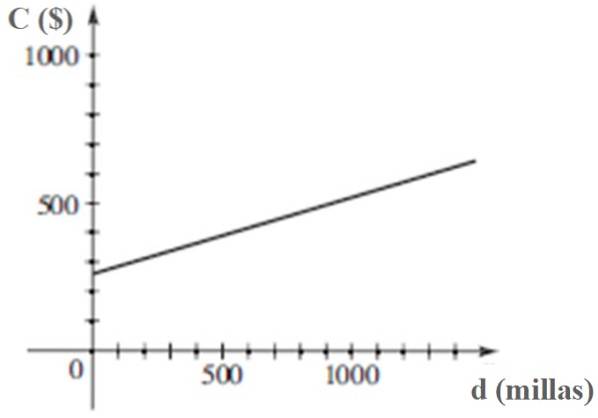
c) De grafiek van C versus d.

Oplossing voor

Stel dat de variabelen een relatie hebben die wordt gegeven door:

C = C_of + Advertentie

Waar A en C_of zijn te bepalen constanten. A is de helling van de lijn die grafisch de relatie tussen C en d weergeeft. Co is de snede met de verticale as, de vaste maandelijkse kost die de bestuurder moet betalen voor het enkele feit dat hij de auto ter beschikking heeft. Denk hierbij bijvoorbeeld aan onderhoudskosten en belastingen.

Om een ​​lijn ondubbelzinnig te bepalen, is het noodzakelijk om de helling te kennen. Hiervoor hebben we de punten:

P.₁: 480 mijl, $ 380

P._twee: 800 mijl, $ 460

Deze punten, van coördinaten (d, C) of (afstand, kosten), zijn analoog aan de punten van coördinaten (x, y) van het Cartesische vlak, wat verandert zijn de namen. De helling A van de lijn wordt dan gegeven door:

A = (C_twee - C₁) / (d_twee - d₁​

A = [(460 - 380) $ / (800 - 480) mijl] = (1/4) $ / mijl

De helling van de lijn geeft de kosten per mijl weer, als volgt:

C = C_of + A.d = Co + (1/4). D

Om de kosten van basis C te bepalen_of Deze vergelijking wordt genomen en een van de punten waarvan we weten dat deze erbij hoort, wordt vervangen, bijvoorbeeld P₁​

380 $ = C_of + [(1/4) $ / mijl]. 480 mijl → 380 $ = C._of + $ 120

C_of = $ 260

Nu kunnen we het lineaire variatiemodel formuleren als:

C = 260 + (1/4) d

Oplossing b

De maandelijkse kosten voor het reizen van 1500 mijlen zijn:

C = 260 + (1/4) x $ 1500 = $ 635

Oplossing c

De grafiek van C versus d is:

Referenties

1. Baldor. 1977. Elementaire algebra. Venezolaanse culturele edities.
2. Hoekenga, C. Lineaire vergelijkingen in de wetenschap. Hersteld van: visionlearning.com.
3. Hoffman, J. Selectie van wiskundeonderwerpen. Deel 2.
4. Jiménez, R. 2008. Algebra. Prentice hal.
5. Stewart, J. 2006. Precalculus: wiskunde voor calculus. 5e. Editie. Cengage leren.
6. Zill, D. 1984. Algebra en trigonometrie. Mcgraw heuvel.