
Vector richtvergelijking van de lijn, opgeloste oefeningen
Het wordt begrepen door directeur vector een die de richting van een lijn definieert, hetzij in het vlak of in de ruimte. Daarom kan een vector parallel aan de lijn worden beschouwd als een sturende vector daarvan.
Dit is mogelijk dankzij een axioma van de Euclidische meetkunde dat zegt dat twee punten een lijn definiëren. Dan definieert het door deze twee punten gevormde georiënteerde segment ook een richtvector van de genoemde lijn.
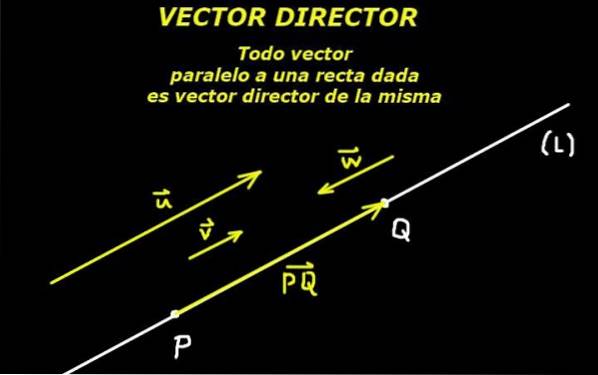
Gegeven een punt P. behorend tot de lijn (L) en kreeg een regisseur vector of van die lijn is de lijn volledig bepaald.
Artikel index
- 1 Vergelijking van de lijn- en richtvector
- 1.1 Parametrische vergelijking van de lijn
- 2 De lijn in vectorvorm
- 2.1 Voorbeeld 2
- 2.2 Doorlopende vorm van de lijn en de directorvector
- 3 Algemene vorm van de vergelijking van de lijn
- 3.1 Voorbeeld 3
- 4 Standaardvorm van de vergelijking van de lijn
- 4.1 Voorbeeld 4
- 5 oefeningen opgelost
- 5.1 -Oefening 1
- 5.2 -Oefening 2
- 6 referenties
Vergelijking van de lijn- en directorvector
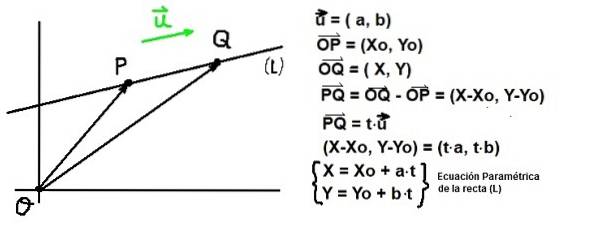
Gegeven een punt P. van coördinaten Vraag: (Xo, I) en een vector of directeur van een straat (L), allemaal punt Q van coördinaten Vraag: (X, Y) moet voldoen aan dat de vector PQ parallel zijn aan u. Deze laatste voorwaarde is gegarandeerd als PQ Is evenredig met of
PQ = t⋅of
in de vorige uitdrukking t is een parameter die bij de reële getallen hoort.
Als de Cartesiaanse componenten van PQ en van of De bovenstaande vergelijking is als volgt geschreven:
(X-Xo, Y-Yo) = t⋅ (een, b)
Als de componenten van vectorgelijkheid gelijk zijn, hebben we het volgende paar vergelijkingen:
X - Xo = a⋅t Y Y - ik = b⋅t
Parametrische vergelijking van de lijn
De coördinaten X en Y van een punt op de lijn (L) passeren door een coördinaatpunt (Xo, I) en het is parallel aan directeur vector of= (a, b) worden bepaald door reële waarden toe te kennen aan de variabele parameter t:
X = Xo + a⋅t; Y = I + b⋅t
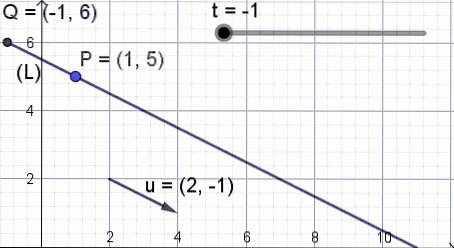
voorbeeld 1
Om de betekenis van de parametervergelijking van de lijn te illustreren, nemen we als richtvector
of = (a, b) = (2, -1)
en als een bekend punt van de lijn het punt
P = (Xo, I) = (1, 5).
De parametervergelijking van de lijn is:
X = 1 + 2⋅t; Y = 5 - 1⋅t; -
Om de betekenis van deze vergelijking te illustreren, wordt figuur 3 getoond, waar de parameter t in waarde en het punt verandert Q van coördinaten (X, Y) neem verschillende posities op het rechte stuk.
De lijn in vectorvorm
Gegeven een punt P op de lijn en zijn richtvector u, kan de vergelijking van de lijn in vectorvorm worden geschreven:
OQ OP + λ⋅of
In de bovenstaande vergelijking is Q elk punt maar behorend tot de lijn en λ een reëel getal.
De vectorvergelijking van de lijn is van toepassing op elk aantal dimensies, zelfs een hyperlijn kan worden gedefinieerd.
In het driedimensionale geval voor een regisseurvector of= (a, b, c) en een punt P = (Xo, Yo, Zo), de coördinaten van een algemeen punt Q = (X, Y, Z) behorend bij de lijn is:
(X EN Z) (Xo, Yo, Zo) + λ⋅ (a, b, c)
Voorbeeld 2
Beschouw opnieuw de lijn die een sturende vector heeft
of = (a, b) = (2, -1)
en als bekend punt van de lijn het punt
P = (Xo, I) = (1, 5).
De vectorvergelijking van deze lijn is:
(X, Y) = (1, 5) + λ⋅ (2, -1)
Doorlopende vorm van de lijn en de regisseur vector
Uitgaande van de parametrische vorm, wissen en gelijk stellen van de parameter λ, hebben we:
(X-Xo) / a = (Y-Yo) / b = (Z-Zo) / c
Dit is de symmetrische vorm van de vergelijking van de lijn. ik voel dat naar, b Y c zijn de componenten van de regisseur vector.
Voorbeeld 3
Beschouw de lijn die een sturende vector heeft
of = (a, b) = (2, -1)
en als bekend punt van de lijn het punt
P = (Xo, I) = (1, 5). Zoek de symmetrische vorm.
De symmetrische of continue vorm van de lijn is:
(X - 1) / 2 = (Y - 5) / (- 1)
Algemene vorm van de vergelijking van de lijn
De vergelijking met de volgende structuur staat bekend als de algemene vorm van de lijn in het XY-vlak:
A⋅X + B⋅Y = C
De uitdrukking voor de symmetrische vorm kan worden herschreven om de algemene vorm te hebben:
b⋅X - a⋅Y = b⋅Xo - a⋅Yo
in vergelijking met de algemene vorm van de lijn is het:
A = b, B = -a en C = b⋅Xo - a⋅Yo
Voorbeeld 3
Zoek de algemene vorm van de lijn waarvan de directorvector u = (2, -1) is
en dat gaat door het punt P = (1, 5).
Om de algemene vorm te vinden kunnen we de gegeven formules gebruiken, maar er zal een alternatief pad worden gekozen.
We beginnen met het vinden van de dubbele vector w van de richtvector u, gedefinieerd als de vector die wordt verkregen door de componenten van u uit te wisselen en de tweede met -1 te vermenigvuldigen:
w= (-1, -2)
de dubbele vector w komt overeen met een rotatie van 90 ° met de klok mee van de richtvector v.
We vermenigvuldigen ons scalair w met (X, Y) en met (Xo, I) en we matchen:
(-1, -2) • (X, Y) = (-1, -2) • (1, 5)
-X-2Y = -1 -2⋅5 = -11
eindelijk overgebleven:
X + 2Y = 11
Standaardvorm van de vergelijking van de lijn
Het staat bekend als de standaardvorm van de lijn in het XY-vlak, een die de volgende structuur heeft:
Y = m⋅X + d
waarbij m de helling voorstelt en d het snijpunt met de Y-as.
Gegeven de richtingsvector u = (a, b), is de helling m b / a.
Y d wordt verkregen door X en Y te vervangen door het bekende punt Xo, I:
Ik = (b / a) Xo + d.
Kortom, m = b / a en d = I - (b / a) Xo
Merk op dat de helling m het quotiënt is tussen de componenten Y van de regisseur vector en de component X van hetzelfde.
Voorbeeld 4
Zoek de standaardvorm van de lijn waarvan de directorvector u = (2, -1) is
en dat gaat door het punt P = (1, 5).
m = -½ en d = 5 - (-½) 1 = 11/2
Y = (-1/2) X + 11/2
Opgeloste oefeningen
-Oefening 1
Zoek een richtvector van de lijn (L) die het snijpunt is van het vlak (Π): X - Y + Z = 3 en het vlak (Ω): 2X + Y = 1.
Schrijf vervolgens de continue vorm van de vergelijking van de lijn (L).
Oplossing
Uit de vergelijking van het vlak (Ω) klaring Y: Y = 1 -2X
Vervolgens vervangen we in de vergelijking van het vlak (Π):
X - (1 - 2X) + Z = 3 ⇒ 3X + Z = 4 ⇒ Z = 4 - 3X
Vervolgens parametriseren we X, we kiezen de parametrering X = λ
Dit betekent dat de lijn een vectorvergelijking heeft die wordt gegeven door:
(X, Y, Z) = (λ, 1 - 2λ, 4 - 3λ)
die kan worden herschreven als:
(X, Y, Z) = (0, 1, 4) + λ (1, -2, -3)
waarmee het duidelijk is dat de vector of = (1, -2, -3) is een sturende vector van de lijn (L).
De doorlopende vorm van de lijn (L) is:
(X - 0) / 1 = (Y - 1) / (- 2) = (Z - 4) / (- 3)
-Oefening 2
Gezien het 5X-vliegtuig + naar Y + 4Z = 5
en de lijn waarvan de vergelijking X / 1 = (Y-2) / 3 = (Z -2) / (- 2) is
Bepaal de waarde van naar zodat het vlak en de lijn parallel zijn.
Oplossing 2
De vector n = (5, a, 4) is een vector loodrecht op het vlak.
De vector of = (1, 3, -2) is een richtvector van de lijn.
Als de lijn evenwijdig is aan het vlak, dan n • v = 0.
(5, naar, 4)(1, 3, -2) = 5 +3naar -8 = 0 ⇒ naar= 1.
Referenties
- Fleming, W., & Varberg, D. E. (1989). Precalculus wiskunde. Prentice Hall PTR.
- Kolman, B. (2006). Lineaire algebra. Pearson Education.
- Leal, J. M., en Viloria, N. G. (2005). Vliegtuig analytische meetkunde. Mérida - Venezuela: Redactie Venezolana C. A.
- Navarro, Rocio. Vectoren. Hersteld van: books.google.co.ve.
- Pérez, C. D. (2006). Voorberekening. Pearson Education.
- Prenowitz, W. 2012. Basisconcepten van geometrie. Rowman & Littlefield.
- Sullivan, M. (1997). Voorberekening. Pearson Education.


Niemand heeft nog op dit artikel gereageerd.