De golf kenmerken zijn de kenmerken van het golffenomeen: golflengte, frequentie, dalen, toppen, snelheid, energie en andere die we in dit artikel zullen uitleggen.
In golven reizen geen deeltjes mee met de storing, maar energie. Wanneer een golf zich voortplant in een materieel medium, dat onder andere water, lucht of een touw kan zijn, bewegen de deeltjes zich nauwelijks uit de evenwichtspositie om er na korte tijd weer naar terug te keren.
De beweging wordt echter van het ene deeltje op het andere overgedragen, waardoor ze allemaal gaan trillen. Op deze manier noemen we de storing Golf, net zoals de golf fans dat doet in stadions, wanneer er voetbalwedstrijden worden gespeeld.
De studie van golven is erg interessant, aangezien we in een wereld vol met golven leven: licht, zeegolven, het geluid van muziek en stem zijn allemaal golfverschijnselen, hoewel van verschillende aard. Zowel licht als geluid zijn bijzonder belangrijk, omdat we ze continu nodig hebben om te communiceren met de buitenwereld..
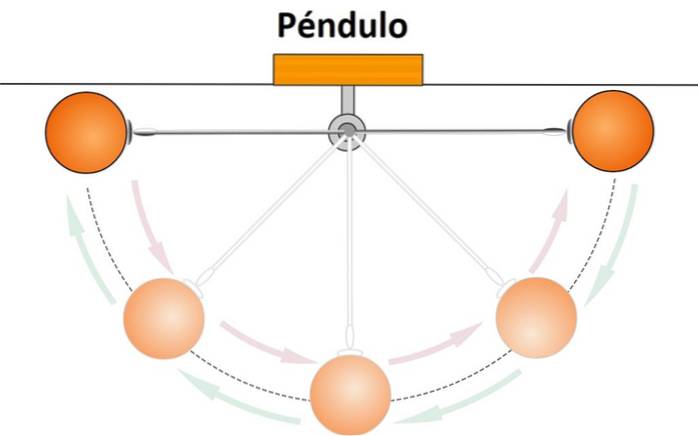
Het is het volledige pad dat een deeltje maakt in zijn heen en weer beweging. Een slinger heeft bijvoorbeeld een heen en weer beweging, aangezien hij vanaf een bepaald punt een boog beschrijft, stopt wanneer hij een bepaalde hoogte bereikt en terugkeert naar zijn oorspronkelijke positie..
Als er geen wrijving was, zou deze beweging voor onbepaalde tijd doorgaan. Maar door wrijving wordt de beweging langzamer en minder breed, totdat de slinger stopt..
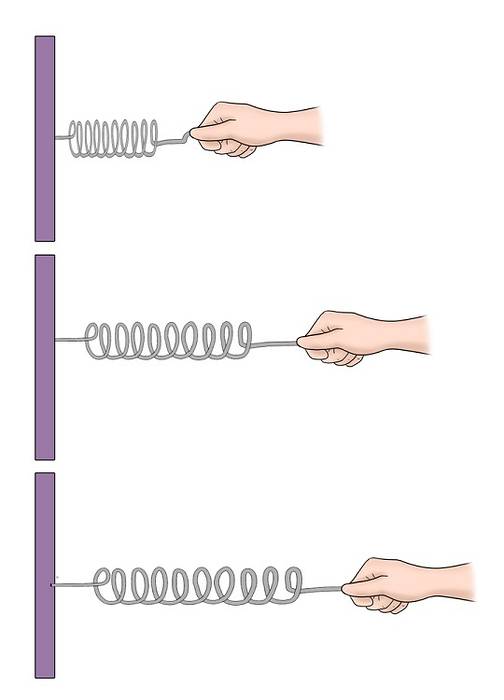
Wanneer een horizontale strakke snaar wordt verstoord, trillen de deeltjes van de snaar in verticale richting, dat wil zeggen van boven naar beneden, terwijl de verstoring horizontaal langs de snaar beweegt.
Wanneer een deeltje heen en weer beweegt, doet het dit door rond een bepaald punt te bewegen, de oorsprong of het centrum van oscillatie genoemd..
In het voorbeeld van de slinger is hij in evenwicht op het laagste punt, en hij oscilleert eromheen als we hem een beetje van deze positie scheiden. Daarom kan dit punt worden beschouwd als het middelpunt van de oscillatie.
We kunnen ons ook een veer voorstellen op een horizontale tafel, aan het ene uiteinde aan een muur bevestigd en met een blok aan het andere uiteinde. Als het veerbloksysteem ongestoord is, bevindt het blok zich in een bepaalde evenwichtspositie.
Door de veer echter een beetje in te drukken of uit te rekken, begint het systeem rond die evenwichtspositie te oscilleren..
Het is de afstand waarover het deeltje zich na een tijdje van het oscillatiecentrum verwijdert. Het wordt gemeten in meters wanneer het SI International System wordt gebruikt..
Als een veer met een blok aan het ene uiteinde wordt samengedrukt of uitgerekt, wordt er gezegd dat deze een verlenging heeft ondergaan van "x" aantal meters, centimeters of welke eenheid dan ook wordt gebruikt om de afstand te meten..
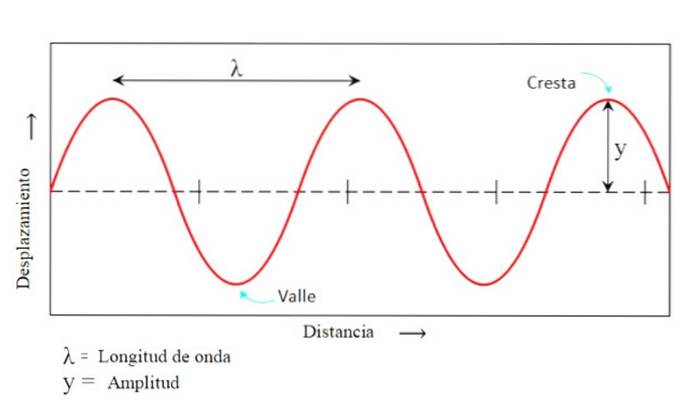
Het zijn respectievelijk de hoogste en laagste punten die het deeltje bereikt ten opzichte van de evenwichtspositie y = 0 (zie figuur 1).
Het is de maximale afstand die het deeltje scheidt van het oscillatiecentrum en wordt ook gegeven in meters. Het wordt aangeduid als NAAR of zoals Y. Daar valt de evenwichtspositie samen met y = 0 en komt overeen met de toppen en dalen van de golf.
Amplitude is een belangrijke parameter, omdat het verband houdt met de energie die door de golf wordt gedragen. Hoe groter de amplitude, hoe groter de energie, zoals bijvoorbeeld gebeurt bij oceaangolven.
De knooppunten zijn de punten waarop het deeltje door het middelpunt van oscillatie of evenwichtspositie gaat..
Dit is wat een volledige oscillatie wordt genoemd, wanneer het deeltje van de ene top naar de andere gaat, of van de ene vallei naar de andere. Dus we zeggen dat het fietste.
De slinger maakt een volledige zwaai wanneer hij een bepaalde hoogte van de evenwichtspositie af beweegt, door het laagste punt gaat, op de heenreis naar dezelfde hoogte stijgt en op de terugreis terugkeert naar de beginhoogte.
Omdat de golven zich herhalen, is de beweging van de deeltjes periodiek. De periode is de tijd die nodig is om een volledige oscillatie uit te voeren en wordt meestal aangeduid met de hoofdletter T. De eenheden van de periode in het SI International System zijn de seconde (n).
Het is de omgekeerde of wederkerige grootte van de periode en is gerelateerd aan het aantal oscillaties of cycli dat per tijdseenheid wordt uitgevoerd. Het wordt aangegeven met de letter F..
Omdat het aantal trillingen geen eenheid is, worden seconden gebruikt voor frequentie-1 (s-1), genaamd Hertz of hertz en afgekort Hz.
Omdat we het omgekeerde van de periode zijn, kunnen we een wiskundige relatie tussen beide grootheden schrijven:
f = 1 / T
O goed:
T = 1 / f
Als een slinger bijvoorbeeld 30 cycli in 6 seconden uitvoert, is de frequentie:
f = (30 cycli) / (6 s) = 5 cycli / s = 5 Hz.
Het is de afstand tussen twee punten van een golf die zich op dezelfde hoogte bevinden, mits er een volledige trilling is gemaakt. Het kan bijvoorbeeld van de ene bergkam naar de andere in een rij worden gemeten, maar ook van dal tot dal.
Golflengte wordt aangeduid met de Griekse letter λ, die wordt gelezen als "lambda" en wordt gemeten in afstandseenheden zoals meters in het internationale systeem, hoewel er zo'n grote verscheidenheid aan golflengten is dat veelvouden en deelvouden vaak voorkomen.
Het is de omgekeerde grootte van de golflengte, vermenigvuldigd met het getal 2π. Daarom hebben we bij het aanduiden van het golfnummer met de letter k:
k = 2π / λ
Het is de snelheid waarmee de storing zich verplaatst. Als het medium waarin de golf zich voortplant homogeen en isotroop is, dat wil zeggen dat de eigenschappen overal hetzelfde zijn, dan is deze snelheid constant en wordt gegeven door:
v = λ / T
De eenheden voor voortplantingssnelheid zijn dezelfde als voor elke andere snelheid. In het internationale systeem komt het overeen met m / s.
Omdat de periode het omgekeerde is van de frequentie, kan deze ook worden uitgedrukt:
v = λ. F.
En aangezien de snelheid constant is, is het product λ.f ook constant, zodat als bijvoorbeeld de golflengte wordt gewijzigd, de frequentie verandert zodat het product hetzelfde blijft.
Niemand heeft nog op dit artikel gereageerd.