Zwaartekrachtversnelling wat het is, hoe het wordt gemeten en oefeningen

De versnelling van de zwaartekracht of zwaartekrachtversnelling wordt gedefinieerd als de intensiteit van het zwaartekrachtveld van de aarde. Dat wil zeggen, de kracht die het uitoefent op een object, per massa-eenheid.

Het wordt aangeduid met de nu bekende letter g en de geschatte waarde in de buurt van het aardoppervlak is 9,8 m / s^twee. Deze waarde kan kleine variaties ondergaan met de geografische breedtegraad en ook met de hoogte ten opzichte van zeeniveau..

De versnelling van de zwaartekracht heeft, naast de bovengenoemde grootte, richting en zin. Het is inderdaad verticaal gericht naar het middelpunt van de aarde.

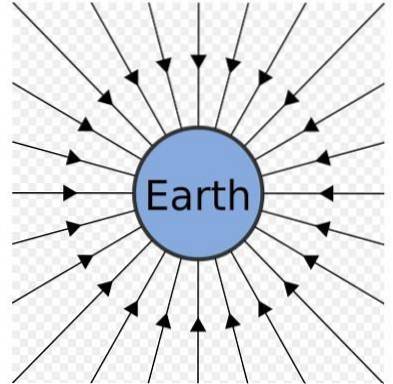
Het zwaartekrachtveld van de aarde kan worden weergegeven als een reeks radiale lijnen die naar het midden wijzen, zoals weergegeven in de vorige afbeelding.

Artikel index

• 1 Wat is de versnelling van de zwaartekracht?
  • 1.1 De wet van universele zwaartekracht
• 2 Hoe wordt de zwaartekracht gemeten op verschillende planeten?
  • 2.1 Experimenteer om de waarde van g te bepalen
  • 2.2 Standaardwaarde van g op aarde, op de maan en op Mars
  • 2.3 Zwaartekracht op de maan
  • 2.4 Zwaartekracht op Mars
• 3 Oefening opgelost: de vallende appel
• 4 referenties

Wat is de versnelling van de zwaartekracht?

De waarde van de versnelling van de zwaartekracht op aarde of op een andere planeet is gelijk aan de intensiteit van het zwaartekrachtveld dat het produceert, dat niet afhankelijk is van de objecten eromheen, maar alleen van zijn eigen massa en straal..

De versnelling van de zwaartekracht wordt vaak gedefinieerd als de versnelling die wordt ervaren door een object in vrije val in de buurt van het aardoppervlak..

In de praktijk is dit wat bijna altijd gebeurt, zoals we zullen zien in de volgende paragrafen, waarin de wet van universele zwaartekracht van Newton zal worden gebruikt..

Newton zou deze beroemde wet hebben ontdekt tijdens het mediteren op vallende lichamen onder een boom. Toen hij de slag van de appel op zijn hoofd voelde, wist hij meteen dat de kracht die de appel doet vallen dezelfde is die ervoor zorgt dat de maan in een baan om de aarde draait..

De wet van universele zwaartekracht

Of de legende van de appel waar was of niet, Newton realiseerde zich dat de grootte van de aantrekkingskracht tussen twee objecten, bijvoorbeeld tussen de aarde en de maan, of de aarde en de appel, afhankelijk moet zijn van hun massa.:

Kenmerken van de zwaartekracht

De zwaartekracht is altijd aantrekkelijk; dat wil zeggen, de twee lichamen die het beïnvloedt, trekken elkaar aan. Het tegenovergestelde is niet mogelijk, aangezien de banen van de hemellichamen gesloten of open zijn (bijvoorbeeld kometen) en een afstotende kracht nooit een gesloten baan kan produceren. Dus de massa trekt altijd aan, wat er ook gebeurt.

Een redelijk goede benadering van de ware vorm van de aarde (m₁) En van de maan of de appel (m_twee) is om aan te nemen dat ze een bolvorm hebben. De volgende afbeelding is een weergave van dit fenomeen.

Hier zowel de kracht uitgeoefend door m₁ Ongeveer m_twee, zoals degene die m_twee Ongeveer m₁, beide van gelijke grootte en gericht langs de lijn die de middelpunten met elkaar verbindt. Ze zijn niet geannuleerd, omdat ze op verschillende objecten worden toegepast.

In alle volgende paragrafen wordt aangenomen dat de objecten homogeen en bolvormig zijn, daarom valt hun zwaartepunt samen met hun geometrische middelpunt. Aangenomen kan worden dat alle massa daar geconcentreerd is.

Hoe meet je de zwaartekracht op verschillende planeten?

De zwaartekracht kan worden gemeten met een gravimeter, een zwaartekrachtmeetapparaat dat wordt gebruikt in geofysische gravimetrische onderzoeken. Momenteel zijn ze veel geavanceerder dan de originelen, maar in het begin waren ze gebaseerd op de slinger.

De slinger bestaat uit een dun, licht en onrekbaar touw van lengte L. Een van de uiteinden is bevestigd aan een steun en een massa m wordt aan de andere opgehangen..

Wanneer het systeem in evenwicht is, hangt de massa verticaal, maar wanneer het ervan wordt gescheiden, begint het te oscilleren en maakt het een heen en weer gaande beweging. De zwaartekracht is er verantwoordelijk voor. Voor alles wat volgt, is het geldig om aan te nemen dat de zwaartekracht de enige kracht is die op de slinger inwerkt.

De periode T van oscillatie van de slinger voor kleine oscillaties wordt gegeven door de volgende vergelijking:

Experimenteer om de waarde van te bepalen g

Materialen

- 1 metalen bal.

- Touw van verschillende lengtes, minimaal 5.

- Meetlint.

- Transportband.

- Chronometer.

- Een beugel om de slinger te bevestigen.

- Ruitjespapier of computerprogramma met spreadsheet.

Werkwijze

1. Selecteer een van de snaren en monteer de slinger. Meet de lengte van de string + de straal van de bol. Dit wordt de lengte L.
2. Haal de slinger ongeveer 5 graden uit de evenwichtspositie (meet hem met de gradenboog) en laat hem slingeren.
3. Start tegelijkertijd de stopwatch en meet de tijd van 10 oscillaties. Schrijf het resultaat op.
4. Herhaal bovenstaande procedure voor de andere lengtes.
5. Zoek de tijd T die de slinger nodig heeft om te zwaaien (elk van de bovenstaande resultaten door 10 delen).
6. Kwadraat elke verkregen waarde en verkrijg T^twee
7. Teken op ruitjespapier elke waarde van T uit^twee op de verticale as, tegen de respectieve waarde van L op de horizontale as. Wees consistent met de eenheden en vergeet niet rekening te houden met de beoordelingsfout van de gebruikte instrumenten: meetlint en stopwatch..
8. Trek de beste lijn die bij de geplotte punten past.
9. Zoek de helling m van genoemde lijn met behulp van twee punten die erbij horen (niet noodzakelijk experimentele punten). Voeg de experimentele fout toe.
10. De bovenstaande stappen kunnen worden uitgevoerd met een spreadsheet en de mogelijkheid om een ​​rechte lijn te construeren en te plaatsen.
11. Van de waarde van de helling naar duidelijk de waarde van g met zijn respectievelijke experimentele onzekerheid.

Standaardwaarde van g op aarde, op de maan en op Mars

De standaardwaarde van zwaartekracht op aarde is: 9,81 m / s^twee, op 45º noorderbreedte en op zeeniveau. Omdat de aarde geen perfecte bol is, zijn de waarden van g enigszins variëren, hoger bij de polen en lager bij de evenaar.

Degenen die de waarde in hun omgeving willen weten, kunnen deze geactualiseerd vinden op de website van het Duitse Metrologie-instituut PTB (Physikalisch-Technische Bundesanstalt), in de sectie Gravity Information System (KRIJT).

Zwaartekracht op de maan

Het zwaartekrachtveld van de maan is bepaald door radiosignalen te analyseren van ruimtesondes die in een baan om de satelliet draaien. De waarde op het maanoppervlak is 1,62 m / s^twee

Zwaartekracht op Mars

De waarde van g_P. voor een planeet hangt het als volgt af van zijn massa M en zijn straal R:

Daarom:

Voor de planeet Mars zijn de volgende gegevens beschikbaar:

M = 6,4185 x 10^{2. 3} kg

R = 3390 km

G = 6,67 x 10^-elf N.m^twee/ kg^twee

Met deze gegevens weten we dat de zwaartekracht van Mars 3,71 m / s is^twee. Uiteraard kan dezelfde vergelijking worden toegepast op de gegevens van de maan of een andere planeet en zo de waarde van de zwaartekracht schatten.

Oefening opgelost: de vallende appel

Stel dat zowel de aarde als een appel bolvormig zijn. De massa van de aarde is M = 5,98 x 10²⁴ kg en de straal is R = 6,37 x 10⁶  m. De massa van de appel is m = 0,10 kg. Stel dat er geen andere kracht is dan de zwaartekracht. Zoek uit de wet van universele zwaartekracht van Newton:

a) De zwaartekracht die de aarde op de appel uitoefent.

b) De versnelling die de appel ervaart wanneer hij van een bepaalde hoogte wordt losgelaten, volgens de tweede wet van Newton.

Oplossing

a) De appel (zogenaamd bolvormig, zoals de aarde) heeft een zeer kleine straal in vergelijking met de straal van de aarde en is ondergedompeld in zijn zwaartekrachtveld. De volgende afbeelding is duidelijk niet op schaal, maar er is een diagram van het zwaartekrachtveld g, en de kracht F. uitgeoefend door de aarde op de appel:

Door de wet van universele zwaartekracht van Newton toe te passen, kan de afstand tussen de centra ongeveer als dezelfde waarde worden beschouwd als de straal van de aarde (de hoogte van waaruit de appel valt, is ook verwaarloosbaar in vergelijking met de straal van de aarde). Daarom:

b) Volgens de tweede wet van Newton is de grootte van de kracht die op de appel wordt uitgeoefend:

F = ma = mg

Waarvan de waarde 0,983 N is, volgens de vorige berekening. Door beide waarden gelijk te stellen en vervolgens de grootte van de versnelling op te lossen, krijgen we:

mg = 0,983 N

g = 0,983 N / 0,10 kg = 9,83 m / s^twee

Dit is een zeer goede benadering van de standaardwaarde van de zwaartekracht.

Referenties

1. Giancoli, D. (2006). Fysica: principes met toepassingen. Zesde editie. Prentice Hall. 118-122.
2. Hewitt, Paul. (2012). Conceptuele fysische wetenschappen. Vijfde editie. Pearson. 91 - 94.
3. Rex, A. (2011). Fundamentals of Physics. Pearson. 213-221.