Vrije val concept, vergelijkingen, opgeloste oefeningen

De vrije val het is de verticale beweging die een object ervaart wanneer het van een bepaalde hoogte dicht bij het aardoppervlak valt. Het is een van de eenvoudigste en meest directe bewegingen die we kennen: in een rechte lijn en met constante versnelling.

Alle voorwerpen die vallen, of die verticaal omhoog of omlaag worden geworpen, bewegen met een versnelling van 9,8 m / s^twee geleverd door de zwaartekracht van de aarde, ongeacht de massa.

Tegenwoordig kan dit feit zonder problemen worden aanvaard. Het duurde echter even om de ware aard van vrije val te begrijpen. De Grieken hadden het al in de 4e eeuw voor Christus op een zeer basale manier beschreven en geïnterpreteerd..

Artikel index

• 1 Bewegingsvergelijkingen van vrije val
  • 1.1 Kinematische grootheden
  • 1.2 Snelheid als functie van verplaatsing
• 2 Voorbeelden van vrije val
  • 2.1 Versnelling
  • 2.2 Positie als functie van de tijd: y (t)
  • 2.3 Snelheid als functie van de tijd: v (t)
  • 2.4 Snelheid als functie van verplaatsing
  • 2.5 Het verticale overgeven
• 3 Opgeloste oefeningen
  • 3.1 Oefening 1
  • 3.2 Oefening 2
• 4 referenties

Vergelijkingen voor vrije valbeweging

Als je er eenmaal van overtuigd bent dat de versnelling hetzelfde is voor alle lichamen die vrijkomen onder invloed van de zwaartekracht, is het tijd om de vergelijkingen vast te stellen die nodig zijn om deze beweging te verklaren..

Het is belangrijk om te benadrukken dat in dit eerste bewegingsmodel geen rekening wordt gehouden met luchtweerstand. De resultaten van dit model zijn echter zeer nauwkeurig en dicht bij de werkelijkheid..

In alles wat volgt, wordt uitgegaan van het deeltjesmodel, dat wil zeggen dat er geen rekening wordt gehouden met de afmetingen van het object, ervan uitgaande dat alle massa geconcentreerd is in een enkel punt.

Voor een gelijkmatig versnelde rechtlijnige beweging in verticale richting wordt de y-as als referentieas genomen. De positieve richting wordt naar boven genomen en de negatieve richting naar beneden..

De kinematische grootheden

Op deze manier zijn de vergelijkingen van positie, snelheid en versnelling als functie van de tijd:

Versnelling

a = g = -9,8 m / s^twee (-32 ft / s^twee​

Positie als functie van de tijd: en (t)

y = y_of + v_of . t + ½ gt^twee

Waar en_of is de beginpositie van de mobiel en v_of is de beginsnelheid. Onthoud dat bij de verticale opwaartse worp de beginsnelheid noodzakelijkerwijs anders is dan 0.

Die kan worden geschreven als:

en en_of = v_of . t + ½ gt^twee

Δy = v_of . t + ½ gt^twee

Met ΔY zijnde de verplaatsing die wordt bewerkstelligd door het mobiele deeltje. In eenheden van het internationale systeem worden zowel de positie als de verplaatsing gegeven in meters (m).

Snelheid als functie van de tijd: v (t)

v = v_of + g. t

Snelheid als functie van verplaatsing

Het is mogelijk om een ​​vergelijking af te leiden die de verplaatsing koppelt aan de snelheid, zonder dat de tijd erin tussenkomt. Hiervoor wordt de tijd van de laatste vergelijking gewist:

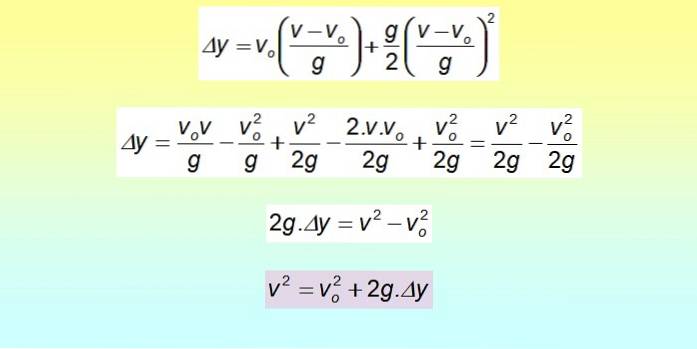
Δy = v_of . t + ½ gt^twee

Het vierkant is ontwikkeld met behulp van het opmerkelijke product en termen worden gehergroepeerd.

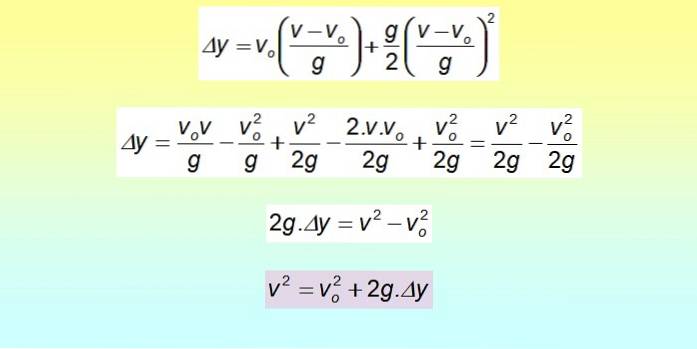
Deze vergelijking is handig als je geen tijd hebt, maar in plaats daarvan snelheden en verplaatsingen, zoals je zult zien in het gedeelte over opgeloste voorbeelden..

Voorbeelden van vrije val

De oplettende lezer zal de aanwezigheid van de beginsnelheid v hebben opgemerkt_of. De voorgaande vergelijkingen zijn geldig voor verticale bewegingen onder invloed van de zwaartekracht, zowel wanneer het object van een bepaalde hoogte valt, als wanneer het verticaal omhoog of omlaag wordt gegooid..

Wanneer het object is gevallen, is het gewoon klaar v_of = 0 en de vergelijkingen worden als volgt vereenvoudigd.

Versnelling

a = g = -9,8 m / s^twee (-32 ft / s^twee​

Positie als functie van de tijd: en (t)

y = y_of+ ½ gt^twee

Snelheid als functie van de tijd: v (t)

v = g. t

Snelheid als functie van verplaatsing

v^twee = 2 g. Dy

Dy zal ook negatief zijn, aangezien v^twee het moet een positieve hoeveelheid zijn. Dit gebeurt ongeacht of u de bron of nul coördinatensysteem op het lanceerpunt of op de grond.

Als de lezer daar de voorkeur aan geeft, kan hij de neerwaartse richting positief nemen. De zwaartekracht zal blijven werken als wordt aangenomen dat deze + 9,8 m / s is^twee. Maar je moet wel consistent zijn met de geselecteerde tekenconventie.

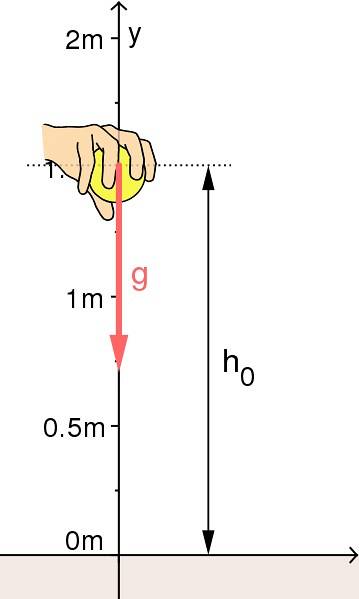
De verticale overgeven

Hier kan de beginsnelheid natuurlijk niet nul zijn. Je moet het object een impuls geven om op te staan. Afhankelijk van de geleverde beginsnelheid zal het object naar een grotere of kleinere hoogte stijgen.

Natuurlijk komt er een moment waarop het object even stopt. Dan is de maximale hoogte vanaf het lanceerpunt bereikt. Evenzo is de versnelling nog steeds g naar beneden. Laten we eens kijken wat er in dit geval gebeurt.

Berekening van de maximaal bereikte hoogte

I = 0 kiezen:

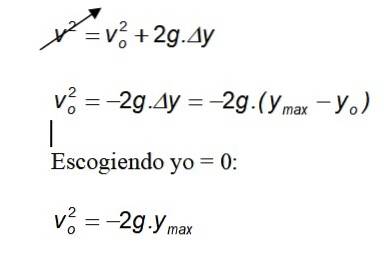
Omdat de zwaartekracht altijd in negatieve richting naar de grond wijst, vervalt het minteken.

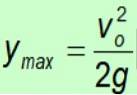
Berekening van de maximale tijd

Een vergelijkbare procedure wordt gebruikt om de tijd te vinden die het object nodig heeft om de maximale hoogte te bereiken.

v = v_of + g. t

Het doet v = 0

v_of = - g. t_{max. hoogte}

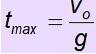
Vliegtijd is hoe lang het object in de lucht blijft. Als het object terugkeert naar het startpunt, is de stijgtijd gelijk aan de daaltijd. Daarom is de vliegtijd 2 t max.

Is het tweemaal de t_{max. hoogte} de totale tijd dat het object in de lucht blijft? Ja, zolang het object begint vanaf een punt en ernaar terugkeert.

Als de lancering wordt gemaakt vanaf een bepaalde hoogte boven de grond en het object mag ernaartoe, zal de vliegtijd niet langer tweemaal de maximale tijd zijn.

Opgeloste oefeningen

Bij de oplossing van de oefeningen die volgen, wordt het volgende in overweging genomen:

1-De hoogte vanaf waar het object valt, is klein in vergelijking met de straal van de aarde.

2-Luchtweerstand is verwaarloosbaar.

3-De waarde van de versnelling van de zwaartekracht is 9,8 m / s^twee

4-Als het gaat om problemen met een enkele mobiele telefoon, wordt bij voorkeur gekozen en_of = 0 op het startpunt. Dit maakt berekeningen meestal gemakkelijker..

5-Tenzij anders vermeld, wordt de verticale opwaartse richting als positief beschouwd.

6-In de gecombineerde opgaande en neergaande bewegingen bieden de toegepaste vergelijkingen direct de juiste resultaten, zolang de consistentie met de tekens behouden blijft: opwaarts positief, neerwaarts negatief en zwaartekracht -9,8 m / s^twee of -10 m / s^twee als afronding de voorkeur heeft (gemakshalve bij het berekenen).

Oefening 1

Een bal wordt verticaal naar boven geworpen met een snelheid van 25,0 m / s. Beantwoord de volgende vragen:

a) Hoe hoog is?

b) Hoe lang duurt het om je hoogste punt te bereiken?

c) Hoe lang duurt het voordat de bal het aardoppervlak raakt nadat deze het hoogste punt heeft bereikt?

d) Wat is uw snelheid wanneer u terugkeert naar het niveau waar u begon?

Oplossing

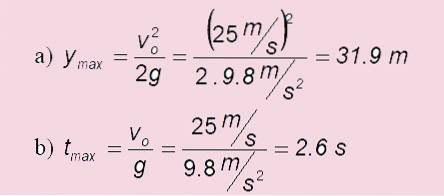
c) In het geval van een levelstart: t_vlucht = 2. t_{max. hoogte} = 2 x6 s = 5,1 s

d) Wanneer het terugkeert naar het startpunt, heeft de snelheid dezelfde grootte als de beginsnelheid, maar in tegengestelde richting, daarom moet deze - 25 m / s zijn. Het is gemakkelijk te controleren door waarden in de vergelijking voor snelheid te vervangen:

Oefening 2

Een kleine postzak wordt losgelaten uit een helikopter die met een constante snelheid van 1,50 m / s naar beneden gaat. Bereken na 2,00 s:

a) Wat is de snelheid van de koffer?

b) Hoe ver is de koffer onder de helikopter?

c) Wat zijn uw antwoorden voor onderdeel a) en b) als de helikopter opstijgt met een constante snelheid van 1,50 m / s?

Oplossing

Paragraaf a

Bij het verlaten van de helikopter draagt ​​de tas dus de beginsnelheid van de helikopter v_of = -1,50 m / s. Met de aangegeven tijd is de snelheid toegenomen dankzij de versnelling van de zwaartekracht:

v = v_of + g. t = -1,50 - (9,8 x 2) m / s = - 21,1 m / s

Sectie b

Laten we eens kijken hoeveel de koffer in die tijd is gevallen vanaf het startpunt:

Koffer: Dy = v_of . t + ½ gt^twee = -1,50 x 2 + ½ (-9,8) x 2^twee m = -22,6 m

Is geselecteerd Y_of = 0 op het startpunt, zoals aangegeven aan het begin van de sectie. Het minteken geeft aan dat de koffer 22,6 m onder het startpunt is gezakt..

Ondertussen de helikopter Het is gevallen met een snelheid van -1,50 m / s gaan we uit van constante snelheid, dus in de aangegeven tijd van 2 seconden heeft de helikopter gereisd:

Helikopter: Δy = v_of.t = -1,50 x 2 m = -3 m.

Daarom zijn de koffer en de helikopter na 2 seconden gescheiden door een afstand van:

d =​-22,6 - (-3) ​m = 19,6 m.

Afstand is altijd positief. Om dit feit te benadrukken, wordt de absolute waarde gebruikt.

Sectie c

Als de helikopter opstijgt, heeft hij een snelheid van + 1,5 m / s. Met die snelheid komt de koffer naar buiten, zodat hij na 2 s al heeft:

v = v_of + g. t = +1,50 - (9,8 x 2) m / s = - 18,1 m / s

De snelheid blijkt negatief, aangezien de tas na 2 seconden naar beneden beweegt. Het is toegenomen dankzij de zwaartekracht, maar niet zoveel als in sectie a.

Laten we nu eens kijken hoeveel de koffer is gedaald vanaf het startpunt tijdens de eerste 2 seconden van de reis:

Zak: Δy = v_of . t + ½ gt^twee = +1,50 x 2 + ½ (-9,8) x 2^twee m = -16,6 m

Ondertussen de helikopter Is gestegen met betrekking tot het startpunt, en heeft het gedaan met constante snelheid:

Helikopter: Δy = v_of.t = +1,50 x 2 m = +3 m.

Na 2 seconden zijn de koffer en de helikopter gescheiden door een afstand van:

d =​-16.6 - (+3) ​m = 19,6 m

De afstand die ze scheidt, is in beide gevallen hetzelfde. In het tweede geval legt de koffer minder verticale afstanden af, omdat de beginsnelheid naar boven was gericht..

Referenties

1. Kirkpatrick, L. 2007. Natuurkunde: een blik op de wereld. 6^ta Verkorte editie. Cengage leren. 23 - 27.
2. Rex, A. 2011. Fundamentals of Physics. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14^th. Ed. Deel 1. 50 - 53.
4. Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9^na Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Physics 10. Pearson Education. 133 - 149.