
Eigenschappen van eenheidscellen, netwerkconstanten en typen
De eenheidscel Het is een denkbeeldige ruimte of regio die de minimale uitdrukking van een geheel vertegenwoordigt; dat in het geval van chemie het geheel een kristal zou zijn dat is samengesteld uit atomen, ionen of moleculen, die zijn gerangschikt volgens een structureel patroon.
In het dagelijks leven zijn voorbeelden te vinden die dit concept belichamen. Hiervoor is het noodzakelijk om aandacht te besteden aan objecten of oppervlakken die een bepaalde repetitieve volgorde van hun elementen vertonen. Sommige mozaïeken, bas-reliëfs, cassetteplafonds, platen en behang kunnen in algemene termen omvatten wat wordt verstaan onder eenheidscel.
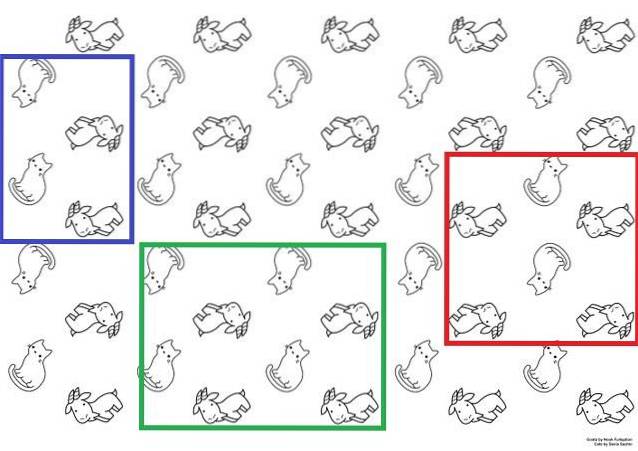
Om het duidelijker te illustreren, is er de afbeelding hierboven die als achtergrond kan worden gebruikt. Daarin verschijnen katten en geiten met twee alternatieve zintuigen; katten staan rechtop of ondersteboven en geiten liggen met hun gezicht naar boven of naar beneden.
Deze katten en geiten zorgen voor een repetitieve structurele opeenvolging. Om het hele papier op te bouwen, zou het voldoende zijn om de eenheidscel een voldoende aantal keren over het oppervlak te reproduceren met behulp van translatiebewegingen..
Mogelijke eenheidscellen worden weergegeven door de blauwe, groene en rode vakjes. Elk van deze drie kan worden gebruikt om de rol te verkrijgen; maar het is nodig om ze op een fantasierijke manier langs het oppervlak te bewegen om erachter te komen of ze dezelfde reeks reproduceren als in de afbeelding.
Te beginnen met de rode doos, zou het duidelijk zijn dat als drie kolommen (van katten en geiten) naar links zouden worden verplaatst, er niet langer twee geiten onderaan zouden verschijnen, maar slechts één. Daarom zou het tot een andere reeks leiden en kan het niet als een eenheidscel worden beschouwd.
Terwijl als ze op een creatieve manier de twee dozen, blauw en groen, zouden verplaatsen, dezelfde volgorde van het papier zou worden verkregen. Beide zijn eenheidscellen; het blauwe vak volgt echter meer de definitie, aangezien het kleiner is dan het groene vak.
Artikel index
- 1 Eigenschappen van eenheidscellen
- 1.1 Aantal herhalende eenheden
- 2 Welke netwerkconstanten definiëren een eenheidscel?
- 3 soorten
- 3.1 Kubiek
- 3.2 Tetragonal
- 3.3 Orthorhombisch
- 3.4 Monokliniek
- 3.5 Trikliniek
- 3.6 Hex
- 3.7 Trigonal
- 4 referenties
Unit Cell Eigenschappen
Zijn eigen definitie, in aanvulling op het zojuist verklaarde voorbeeld, verduidelijkt verschillende van zijn eigenschappen:
-Als je in de ruimte beweegt, ongeacht de richting, krijg je de volledige vaste stof of kristal. Dit komt omdat, zoals vermeld bij katten en geiten, ze de structurele volgorde reproduceren; wat gelijk is aan de ruimtelijke verdeling van de herhalende eenheden.
-Ze moeten zo klein mogelijk zijn (of weinig volume innemen) in vergelijking met andere mogelijke celopties.
-Ze zijn meestal symmetrisch. Ook wordt de symmetrie ervan letterlijk weerspiegeld in de kristallen van de verbinding; als de eenheidscel van een zout kubisch is, zijn de kristallen kubisch. Er zijn echter kristallijne structuren die worden beschreven met eenheidscellen met vervormde geometrieën..
-Ze bevatten herhalende eenheden, die kunnen worden vervangen door punten, die op hun beurt een zogenaamd rooster in drie dimensies vormen. In het vorige voorbeeld stellen de katten en geiten de roosterpunten voor, gezien vanaf een hoger niveau; dat wil zeggen, twee dimensies.
Aantal herhalende eenheden
De herhalende eenheden of roosterpunten van de eenheidscellen behouden hetzelfde aandeel van de vaste deeltjes.
Als je het aantal katten en geiten in de blauwe doos telt, heb je twee katten en geiten. Hetzelfde gebeurt met de groene doos, en ook met de rode doos (zelfs als al bekend is dat het geen eenheidscel is).
Stel bijvoorbeeld dat katten en geiten respectievelijk G- en C-atomen zijn (een vreemde dierlijke las). Aangezien de verhouding van G tot C 2: 2 of 1: 1 is in het blauwe vak, kan veilig worden verwacht dat de vaste stof de formule GC (of CG) zal hebben.
Wanneer de vaste stof min of meer compacte structuren vertoont, zoals gebeurt met zouten, metalen, oxiden, sulfiden en legeringen, zijn er in de eenheidscellen geen hele repetitieve eenheden; dat wil zeggen, er zijn porties of delen ervan, die samen een of twee eenheden vormen.
Dit is niet het geval voor GC. Als dat zo is, zou het blauwe vak de katten en geiten in tweeën "splitsen" (1 / 2G en 1 / 2C) of vier (1 / 4G en 1 / 4C). In de volgende paragrafen zal worden gezien dat in deze eenheidscellen de reticulaire punten handig op deze en andere manieren zijn verdeeld..
Welke netwerkconstanten definiëren een eenheidscel?
De eenheidscellen in het GC-voorbeeld zijn tweedimensionaal; dit geldt echter niet voor echte modellen die alle drie de dimensies beschouwen. Zo worden de vierkanten of parallellogrammen omgevormd tot parallellepipedums. Nu is de term "cel" logischer.
De afmetingen van deze cellen of parallellepipedums zijn afhankelijk van hoe lang hun respectievelijke zijden en hoeken zijn..
In de onderste afbeelding heb je de onderste achterhoek van het parallellepipedum, samengesteld uit de zijkanten naar, b Y c, en de hoeken α, β en γ.
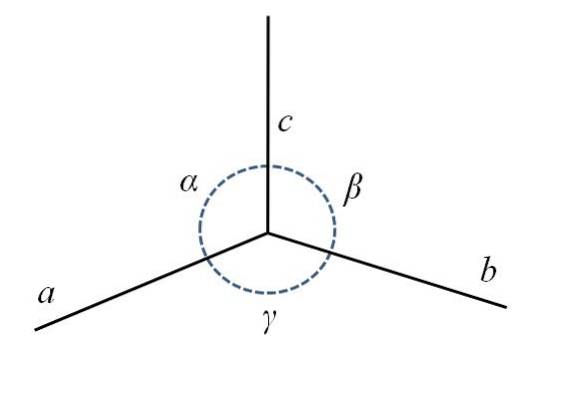
Zoals je kunt zien, naar is iets langer dan b Y c. In het midden is er een gestippelde cirkel om de hoeken α, β en γ aan te geven ac, cb Y ba, respectievelijk. Voor elke eenheidscel hebben deze parameters constante waarden en bepalen ze de symmetrie ervan en die van de rest van het kristal..
Door weer wat verbeeldingskracht toe te passen, zouden de afbeeldingsparameters een kubusachtige cel definiëren die zich op zijn rand uitstrekte. naar. Er ontstaan dus eenheidscellen met verschillende lengtes en hoeken van hun randen, die ook in verschillende typen kunnen worden ingedeeld.
Types
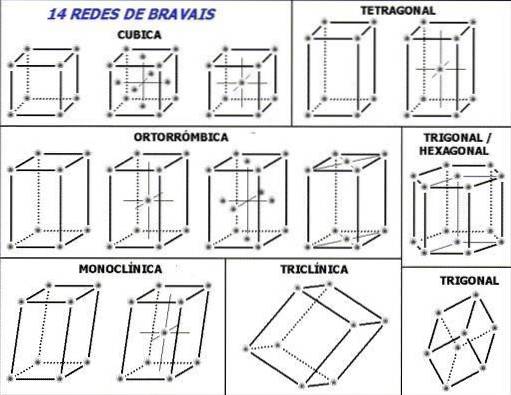
Merk om te beginnen op in de bovenste afbeelding de stippellijnen in de eenheidscellen: ze geven de onderste achterhoek aan, zoals zojuist uitgelegd. De volgende vraag kan gesteld worden: waar zijn de roosterpunten of herhalende eenheden? Hoewel ze de verkeerde indruk wekken dat de cellen leeg zijn, ligt het antwoord op hun hoekpunten.
Deze cellen worden zo gegenereerd of gekozen dat de herhalende eenheden (grijsachtige punten van de afbeelding) zich op hun hoekpunten bevinden. Afhankelijk van de waarden van de parameters die in de vorige sectie zijn vastgesteld, constant voor elke eenheidscel, worden zeven kristalsystemen afgeleid.
Elk kristalsysteem heeft zijn eigen eenheidscel; de tweede definieert de eerste. In de bovenste afbeelding zijn er zeven vierkanten, die overeenkomen met de zeven kristalsystemen; of op een iets meer samengevatte manier, kristallijne netwerken. Een kubieke eenheidscel komt dus bijvoorbeeld overeen met een van de kristalsystemen die een kubisch kristalrooster definieert.
Volgens de afbeelding zijn de kristallijne systemen of netwerken:
-Kubiek
-Tetragonaal
-Orthorhombisch
-Zeshoekig
-Monoclinic
-Triclinic
-Trigonal
En binnen deze kristallijnen systemen ontstaan anderen die de veertien Bravais-netwerken vormen; dat ze van alle kristallijne netwerken de meest basale zijn.
Kubiek
In een kubus zijn al zijn zijden en hoeken gelijk. Daarom geldt in deze eenheidscel het volgende:
naar b c
α = β = γ = 90º
Er zijn drie kubieke eenheidscellen: eenvoudig of primitief, lichaamsgericht (bcc) en gezichtgecentreerd (fcc). De verschillen liggen in de verdeling van de punten (atomen, ionen of moleculen) en in het aantal ervan.
Welke van deze cellen is het meest compact? Degene waarvan het volume meer wordt ingenomen door punten: de kubus gecentreerd op de vlakken. Merk op dat als we de stippen vanaf het begin zouden vervangen door de katten en geiten, ze niet beperkt zouden blijven tot een enkele cel; ze zouden erbij horen en door meerdere worden gedeeld. Nogmaals, het zouden delen van G of C zijn.
Aantal eenheden
Als katten of geiten zich bij de hoekpunten bevonden, zouden ze worden gedeeld door 8 eenheidscellen; dat wil zeggen, elke cel heeft 1/8 van G of C.Voeg acht kubussen samen of stel je voor, in twee kolommen van elk twee rijen, om het te visualiseren.
Als er katten of geiten op de gezichten stonden, zouden ze alleen worden gedeeld door 2 eenheidscellen. Om het te zien, plaatst u gewoon twee kubussen bij elkaar.
Aan de andere kant, als de kat of de geit zich in het midden van de kubus bevonden, zouden ze slechts tot een enkele eenheidscel behoren; Hetzelfde gebeurt met de vakken in de hoofdafbeelding, toen het concept werd aangepakt.
Zei dan het bovenstaande, binnen een eenvoudige kubieke eenheidscel die we hebben een eenheid of roosterpunt, aangezien het 8 hoekpunten heeft (1/8 x 8 = 1). Voor de kubieke cel gecentreerd in het lichaam zijn er: 8 hoekpunten, wat gelijk is aan een atoom, en een punt of eenheid in het midden; daarom is er twee eenheden.
En voor de kubische cel met het midden van het gezicht zijn er: 8 hoekpunten (1) en zes vlakken, waarbij de helft van elk punt of elke eenheid wordt gedeeld (1/2 x 6 = 3); daarom bezit het vier eenheden.
Tetragonaal
Soortgelijke opmerkingen kunnen worden gemaakt met betrekking tot de eenheidscel voor het tetragonale systeem. De structurele parameters zijn de volgende:
naar b c
α = β = γ = 90º
Orthorhombisch
De parameters voor de orthorhombische cel zijn:
naar b c
α = β = γ = 90º
Monoclinic
De parameters voor de monokliene cel zijn:
naar b c
α = γ = 90 °; β ≠ 90º
Triclinic
De parameters voor de triklinische cel zijn:
naar b c
α ≠ β ≠ γ ≠ 90º
Zeshoekig
De parameters voor de zeshoekige cel zijn:
naar b c
a = p = 90 °; γ ≠ 120º
Eigenlijk vormt de cel een derde van een hexagonaal prisma.
Trigonal
En tot slot zijn de parameters voor de trigonale cel:
naar b c
α = β = γ ≠ 90º
Referenties
- Whitten, Davis, Peck & Stanley. (2008). Chemie. (8e ed.). CENGAGE Leren P 474-477.
- Shiver & Atkins. (2008). Anorganische scheikunde. (Vierde druk). Mc Graw Hill.
- Wikipedia. (2019). Primitieve cel. Hersteld van: en.wikipedia.org
- Bryan Stephanie. (2019). Eenheidscel: roosterparameters en kubieke structuren. Studie. Hersteld van: study.com
- Academisch informatiecentrum. (s.f.). Kristalstructuren. [Pdf]. Illinois Institute of Technology. Hersteld van: web.iit.edu
- Belford Robert. (7 februari 2019). Kristalroosters en eenheidscellen. Chemie Libretexts. Hersteld van: chem.libretexts.org



Niemand heeft nog op dit artikel gereageerd.