
Poisson's ratio, formules, waarden, voorbeelden
De Poisson's verhouding het is een dimensieloze hoeveelheid, kenmerkend voor elk materiaal. Het is een indicatie van de vervorming van een stuk materiaal voordat bepaalde krachten worden uitgeoefend.
Wanneer een stuk materiaal dat aan een spanning of compressie wordt blootgesteld, een vervorming ondergaat, is het quotiënt tussen de transversale vervorming en de longitudinale vervorming precies de Poisson-verhouding.
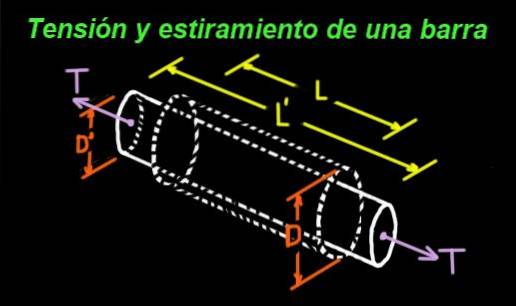
Een rubberen cilinder die aan zijn uiteinden wordt belast, strekt zich bijvoorbeeld uit in de lengterichting, maar versmalt in de dwarsrichting. Figuur 1 toont een staaf waarvan de oorspronkelijke afmetingen zijn: lengte L en diameter D.
De staaf wordt aan zijn uiteinden aan een spanning T onderworpen en als gevolg van deze spanning ondergaat hij een rek, zodat de nieuwe lengte L '> L is. Maar wanneer hij wordt uitgerekt, wordt de diameter ook smaller tot de nieuwe waarde: D' < D.
Het quotiënt tussen de uitrekking (positief) en de versmalling (negatief) vermenigvuldigd met (-1), is een positief getal tussen 0 en 0,5. Dit getal is de zogenaamde Poisson-ratio ν (Griekse letter nu).
Artikel index
- 1 Poisson-verhoudingsformule
- 1.1 Relatie met de elasticiteitsmodulus en de stijfheidsmodulus
- 2 Waarde van de Poisson-verhouding voor materialen
- 3 Rekenvoorbeelden
- 3.1 Voorbeeld 1
- 3.2 Voorbeeld 2
- 4 referenties
Poisson-verhoudingsformule
Om de Poisson-verhouding te berekenen, is het nodig om de longitudinale en transversale rek te bepalen.
De longitudinale rek εL. is de rek gedeeld door de oorspronkelijke lengte:
εL. = (L '- L) / L
Evenzo is de dwarse rek εT is de radiale versmalling gedeeld door de oorspronkelijke diameter:
εT = (D '- D) / D
Daarom wordt de Poisson-verhouding berekend met behulp van de volgende formule:
ν = - εT / εL.
Relatie met elasticiteitsmodulus en stijfheidsmodulus
De verhouding van Poisson ν, is gerelateerd aan de modulus EN elasticiteit (of Young's modulus) en met de modulus van stijfheid G, met behulp van de volgende formule:
ν = E / (2G) - 1
Poisson-verhoudingswaarde voor materialen


Rekenvoorbeelden
voorbeeld 1
Een staaf van een bepaald plastic materiaal heeft een lengte van 150 mm en een cirkelvormige doorsnede van 20 mm in diameter. Bij blootstelling aan een compressiekracht F van 612,25 kg-f wordt een verkorting van 14 mm waargenomen en tegelijkertijd een toename van 0,85 mm in de diameter van de staaf.
Berekenen:
a) Longitudinale rek.
b) De dwarse rek.
c) De Poisson-verhouding van dat materiaal.
d) Young's elasticiteitsmodulus die overeenkomt met het materiaal.
e) De stijfheidsmodulus voor die kunststof.
Oplossing voor
Bedenk dat de longitudinale rek εL de rek is gedeeld door de oorspronkelijke lengte:
εL = (L '- L) / L
εL = (-14 mm) / 150 mm = -0,0933
Merk op dat de longitudinale rek dimensieloos is, en in dit geval negatief omdat er een afname was in de longitudinale dimensie.
Oplossing b
Evenzo is de dwarse rek εT de radiale conus, gedeeld door de oorspronkelijke diameter:
εT = (D '- D) / D
εT = (+0,85 mm) / 20 mm = 0,0425
De dwarse rek is positief omdat de diameter van de staaf is toegenomen.
Oplossing c
Voor de berekening van de Poisson-verhouding moeten we onthouden dat deze wordt gedefinieerd als het negatief van het quotiënt tussen de transversale vervorming en de longitudinale vervorming:
ν = - εT / εL
ν = - 0,0425 / (-0,0933) = 0,4554
Houd er rekening mee dat de Poisson-verhouding een positief dimensieloos getal is en voor de meeste materialen tussen 0 en 0,5 ligt.
Oplossing d
De elasticiteitsmodulus van Young, aangeduid met de letter E, is de evenredigheidsconstante in de wet van Hooke. Door E is de normale spanning σL als volgt gerelateerd aan de rek εL:
σL = E εL
De normaalspanning wordt gedefinieerd als het quotiënt tussen de normaalkracht (in dit geval parallel aan de as van de staaf) en het dwarsdoorsnedegebied:
σL = F / A = F / (π / 4 * D ^ 2)
In deze oefening is de kracht F 612,25 kg-f, die moet worden omgerekend naar newton, de SI-eenheid van kracht:
F = 612,25 kg-f = 612,25 * 9,8 N = 6000 N = 6 kN
Van zijn kant is de doorsnede van gebied A:
A = (π / 4 * D ^ 2) = (3.1416 / 4) * (20 * 10 ^ -3 m) ^ 2 = 3.1416 * 10 ^ -4 m ^ 2
Ten slotte is de normale spanning die op de staaf wordt uitgeoefend:
σL = F / A = 6000 N / 3.1416 * 10 ^ -4 m ^ 2 = 19.098.593 Pa = 19.098 MPa
Om de elasticiteitsmodulus van Young te berekenen, lossen we voor E op uit de wet van Hooke σL = E εL:
E = σL / εL = 19.098.593 Pa / 0,0933 = 204,7 MPa
Oplossing e
De stijfheidsmodulus G is gerelateerd aan Young's modulus E en Poisson's ratio ν door deze formule:
E / (2 G) = 1 + ν
Van daaruit kun je G oplossen:
G = E / (2 (1 + ν)) = 204,7 MPa / (2 (1 + 0,4554)) = 70,33 MPa
Voorbeeld 2
Er is een koperen kabel met een diameter van 4 mm en 1 m lang. Wetende dat de Young-modulus van koper 110.000 MPa is en dat de Poisson-verhouding 0,34 is, schat dan het uitrekken en versmallen in diameter dat de draad ondergaat wanneer er een gewicht van 100 kg-f aan wordt opgehangen..
Oplossing
Ten eerste is het nodig om de normale trekspanning te berekenen die het gewicht op de draad uitoefent, door deze formule te volgen:
σL = F / A = F / (π / 4 * D ^ 2)
De kracht F is 980 N en de doorsnede is:
A = (π / 4 * D ^ 2) = (3.1416 / 4) * (4 * 10 ^ -3 m) ^ 2 = 1.2566 * 10 ^ -5 m ^ 2
Dan is de trekspanning:
σL = 980 N / 1,2566 * 10 ^ -5 m ^ 2 = 77.986.000 Pa
Berekening van draadspanning
De elasticiteitsmodulus van Young, aangeduid met de letter E, is de evenredigheidsconstante in de wet van Hooke die de normale spanning σL relateert aan de rek εL:
σL = E εL
Van daaruit kan de longitudinale rek van de koperdraad worden opgelost:
εL = σL / E = 77,986 MPa / 110000 MPa = 7,09 * 10 ^ -4
Berekening van dwarse rek
Aan de andere kant, om de dwarse rek te kennen, wordt de Poisson-verhouding toegepast:
ν = - εT / εL
Ten slotte hebben we dat de dwarse rek is:
εT = -ν εL = - 0,34 * 7,09 * 10 ^ -4 = -2,41 * 10 ^ -4
Berekening van absolute kabelrek
Ten slotte, om de absolute rek van de kabel te kennen, moet de volgende relatie worden toegepast:
ΔL = εL * L = 7,09 * 10 ^ -4 * 1 m = 7,09 * 10 ^ -4 m = 0,709 mm
Dat wil zeggen, met dat gewicht rekte de kabel nauwelijks 0,709 millimeter.
Berekening van de afname in diameter
Om de absolute krimp in diameter te verkrijgen, gebruiken we de volgende formule:
ΔD = εT * D = -2,41 * 10 ^ -4 * 4 mm = -9,64 * 10 ^ -4 mm = -0,000964 millimeter.
Deze vernauwing in diameter is zo klein dat het moeilijk te zien is met het blote oog, zelfs voor het meten ervan is een zeer nauwkeurig instrument vereist..
Referenties
- Beer F… Mechanica van materialen. 5e. Editie. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Mechanica van materialen. Achtste editie. Prentice Hall. 2011. 3-60.
- Gere J. Mechanica van materialen. Achtste editie. Cengage leren. 4-220.
- Giancoli, D. 2006. Natuurkunde: principes met toepassingen. 6e editie Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Opmerkingen over algemene fysica. UNAM. 87-98.


Niemand heeft nog op dit artikel gereageerd.