
Eenheidscirkel trigonometrische functies en toepassingen
De eenheidscirkel is een cirkel met een straal gelijk aan 1, die gewoonlijk gecentreerd is op het punt (0,0) van het Cartesische coördinatensysteem xy. Wordt gebruikt om eenvoudig de trigonometrische verhoudingen van hoeken te definiëren met behulp van rechthoekige driehoeken.
De vergelijking van de eenheidscirkel met het middelpunt van de oorsprong is:
Xtwee + Ytwee = 1
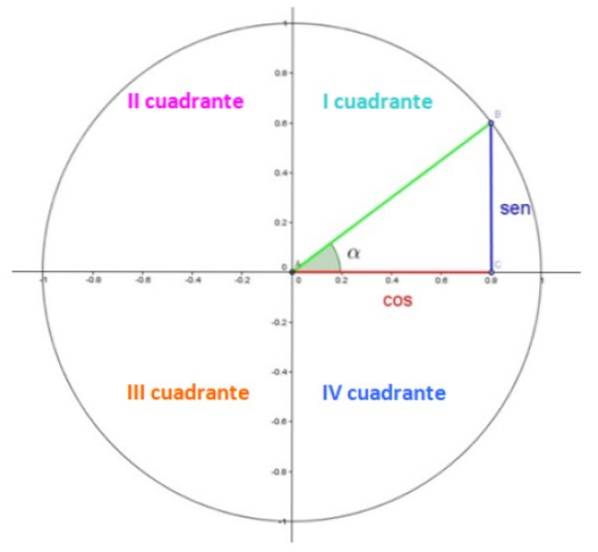
In figuur 1 hebben we de eenheidscirkel, waarin elk kwart in een kwadrant staat. Kwadranten zijn genummerd met Romeinse cijfers en worden tegen de klok in geteld.
In het eerste kwadrant is er een driehoek. De benen, in rood en blauw, meten respectievelijk 0,8 en 0,6, terwijl de hypotenusa in groen 1 meet, aangezien het een straal is.
De scherpe hoek α is een centrale hoek in standaardpositie, wat betekent dat zijn top samenvalt met het punt (0,0) en zijn beginzijde met de positieve x-as. De hoek wordt tegen de klok in gemeten en krijgt volgens afspraak een positief teken.
Welnu, in de eenheidscirkel zijn de cosinus- en sinuscoördinaten van α respectievelijk de x- en y-coördinaten van punt B, die in het getoonde voorbeeld 0,8 en 0,6 zijn..
Van deze twee zijn ze gedefinieerd:
- tg α = sin α / cos α = 0,6 / 0,8 = 0,75
- sec α = 1 / cos α = 1 / 0,8 = 1,25
- cosec α = 1 / sin α = 1 / 0,6 = 1,66 ...
- ctg α = 1 / tg = 0,8 / 0,6 = 1,33…
Artikel index
- 1 Unit Circle-toepassingen
- 1.1 Referentiehoek
- 2 De grafieken van cosinus en sinus uitzetten
- 2.1 Eigenschappen van sinus- en cosinusfuncties
- 3 Opgeloste oefeningen
- 3.1 - Oefening 1
- 3.2 - Oefening 2
- 4 referenties
Unit Circle-toepassingen
Als we ons beperken tot rechthoekige driehoeken, zouden de trigonometrische verhoudingen alleen van toepassing zijn op scherpe hoeken. Met behulp van de eenheidscirkel wordt de berekening van de trigonometrische verhoudingen echter uitgebreid tot elke hoek α.
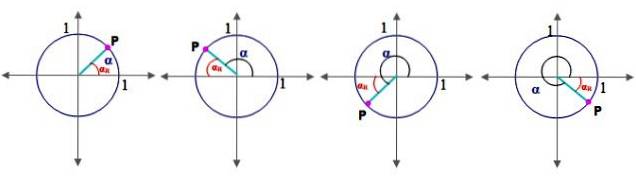
Hiervoor is het noodzakelijk om eerst het concept referentiehoek α te definiërenR
Referentiehoek
Laat α een hoek zijn in de standaardpositie (degene waarvan startzijde valt samen met de positieve x-as), de referentiehoek αR is tussen hem terminal kant en de x-as. Figuur 2 toont de referentiehoek voor hoeken in I, II, III en IV kwadrant.
Voor elk kwadrant wordt de referentiehoek als volgt berekend:
-Eerste kwadrant: αR = α
-Tweede kwadrant: αR = 180º - α
-Derde kwadrant: αR = α - 180º
-Vierde kwadrant: αR = 360º - α
Merk op dat het eerste kwadrant de hoek α samenvalt met zijn referentiehoek. Welnu, de trigonometrische verhoudingen van de hoek α zijn hetzelfde als hun referentiehoek, met de tekens volgens die van de kwadranten waarin de terminale zijde van α valt..
Met andere woorden, de trigonometrische cosinus- en sinusverhoudingen van de hoek α vallen samen met de coördinaten van het punt P, volgens figuur 2.
In de volgende afbeelding zien we de trigonometrische verhoudingen van enkele opmerkelijke hoeken, zoals afgeleid uit de eenheidscirkel.
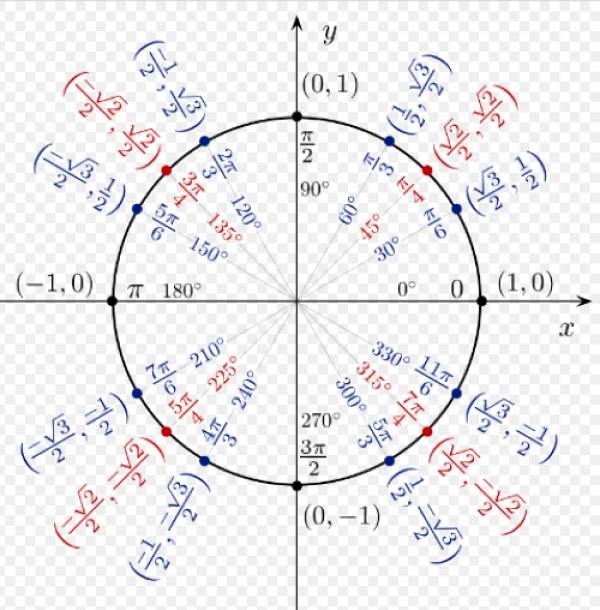
De cosinus- en sinusverhoudingen van elke hoek in het I-kwadrant zijn allemaal positief. Voor α = 60º hebben we de coördinaten (1/2; √3 / 2), die respectievelijk overeenkomen met cos 60º en sin 60º.
De coördinaten van α = 120º zijn (-1/2; √3 / 2), aangezien in het tweede kwadrant de x-coördinaat negatief is.
De cosinus- en sinusgrafieken uitzetten
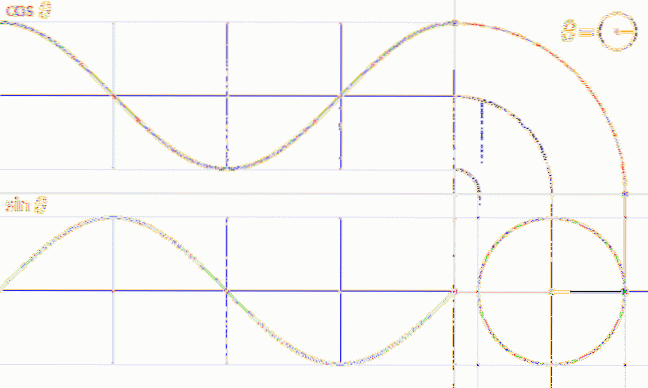
Met behulp van de eenheidscirkel en de coördinaten van de punten P erop, is het mogelijk om de grafieken van de functies cos t en sin t te tekenen, zoals we hieronder zullen zien.
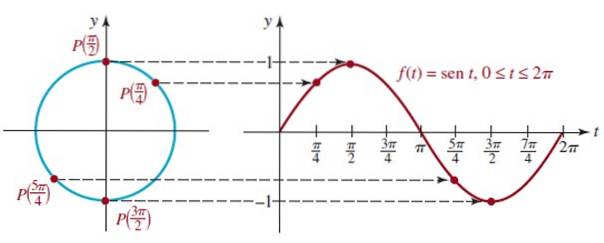
Om dit te doen, bevinden zich verschillende posities van het punt P (t) op de eenheidscirkel. We beginnen met de grafiek van de functie f (t) = sin t.
We kunnen zien dat wanneer we van t = 0 naar t = π / 2 (90º) gaan, de waarde van sin t toeneemt totdat deze 1 bereikt, wat de maximale waarde is.
Aan de andere kant, van t = π / 2 tot t = 3π / 2 neemt de waarde van sin t af van 1 en gaat door 0 op t = π totdat het minimum van -1 bereikt op t = 3π / 2.
De figuur toont de grafiek van de eerste cyclus van f (t) = sin t die overeenkomt met de eerste ronde van de eenheidscirkel, deze functie is periodiek met periode 2π.
Een analoge procedure kan worden uitgevoerd om de grafiek van de functie f (t) = cos t te verkrijgen, zoals weergegeven in de volgende animatie:
Eigenschappen van sinus- en cosinusfuncties
-Beide functies zijn continu in de reeks reële getallen en ook periodiek, van periode 2π.
-Het domein van de functies f (t) = sin t en f (t) = cos t zijn allemaal reële getallen: (-∞, ∞).
-Voor het bereik of pad van sinus en cosinus hebben we het interval [-1,1]. De haakjes geven aan dat -1 en 1 zijn inbegrepen.
- De nullen van sin t zijn de waarden die overeenkomen met nπ met n geheel getal, terwijl de nullen van cos t zijn [(2n + 1) / 2] met n ook geheel getal.
-De functie f (t) = sin t is oneven, het heeft symmetrie rond de oorsprong terwijl de functie cos t even is, de symmetrie is rond de verticale as.
Opgeloste oefeningen
- Oefening 1
Gegeven cos t = - 2/5, wat de horizontale coördinaat is van het punt P (t) op de eenheidscirkel in het tweede kwadrant, verkrijg de overeenkomstige verticale coördinaat sin t.
Oplossing
Aangezien P (t) tot de eenheidscirkel behoort, waarin het waar is dat:
Xtwee + Ytwee = 1
Daarom:
y = ± √ 1 - xtwee
Aangezien P (t) zich in het tweede kwadrant bevindt, wordt de positieve waarde genomen. De verticale coördinaat van punt P (t) is y:
y = √ 1 - (-2/5)twee = √0,84
- Oefening 2
Een wiskundig model voor temperatuur T in graden Fahrenheit op een willekeurige dag, t uur na middernacht wordt het gegeven door:
T (t) = 50 + 10 zonde [(π / 12) × (t - 8)]
Met t tussen 0 en 24 uur. Vind:
a) De temperatuur om 8 uur.
b) Uren waarin T (t) = 60ºF
c) Maximale en minimale temperaturen.
Oplossing voor
We vervangen t = 8 in de gegeven functie:
T (8) = 50 + 10 sin [(π / 12) × (t-8)] = 50 + 10 sin [(π / 12) × (8-8)] =
= 50 + 10 x sin 0 = 50 ºF
Oplossing b
50 + 10 sin [(π / 12) × (t-8)] = 60
Het is een trigonometrische vergelijking en we moeten de onbekende "t" oplossen:
10 sin [(π / 12) × (t-8)] = 60 - 50 = 10
sin [(π / 12) × (t-8)] = 1
We weten dat sin π / 2 = 1, daarom moet het sinusargument 1 zijn:
(π / 12) × (t-8) = π / 2
t-8 = 6
t = 14 uur
Geconcludeerd wordt dat om 14 uur na middernacht de temperatuur 60º is, dat wil zeggen 14.00 uur. Er is geen ander tijdstip gedurende de dag (24 uur) waarop dit gebeurt.
Oplossing c
De maximale temperatuur komt overeen met de waarde waarbij sin [(π / 12) × (t-8)] = 1 en is 60ºF. Aan de andere kant treedt het minimum op als sin [(π / 12) × (t-8)] = -1 en is 40ºF.
Referenties
- Figuera, J. 1999. Mathematics. 1e. Gediversifieerd. Bolivarian Collegiate Editions.
- Hoffman, J. Selectie van wiskundeonderwerpen. Deel 4.
- Jiménez, R. 2008. Algebra. Prentice hal.
- Wiskunde is leuk Eenheidscirkel. Hersteld van: de: mathsisfun.com.
- Wikipedia. Goniometrische identiteiten en formules. Hersteld van: es.wikipedia.org.
- Zill, D. 1984. Algebra en trigonometrie. Mcgraw heuvel.



Niemand heeft nog op dit artikel gereageerd.